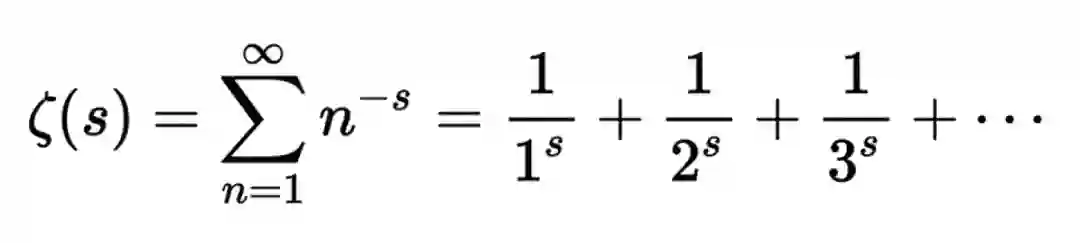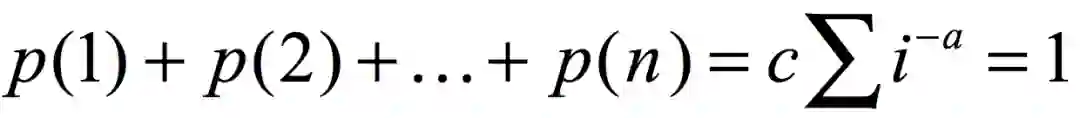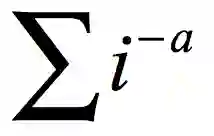黎曼猜想被证明了吗？

黎曼 Zeta 函数可视化

新智元 AI World 2018 世界人工智能峰会

全程回顾

新智元于9月20日在北京国家会议中心举办AI WORLD 2018世界人工智能峰会，邀请机器学习教父、CMU教授 Tom Mitchell，迈克思·泰格马克，周志华，陶大程，陈怡然等AI领袖一起关注机器智能与人类命运。

爱奇艺

上午：https://www.iqiyi.com/v_19rr54cusk.html

下午：https://www.iqiyi.com/v_19rr54hels.html

新浪：http://video.sina.com.cn/l/p/1724373.html

---

  新智元推荐  

来源：集智俱乐部（ID:swarma_org）

作者：集智小编

【新智元导读】近日公布的德国海德堡获奖者论坛日程中，9 月 24 日著名数学家 Michael Atiyah 将会做一场关于 “证明黎曼猜想” 的报告。消息传出，数学物理计算机各路豪杰，纷纷炸了锅。困扰人类 159 年的最重要数学猜想真的要被证明了？

震撼！AI WORLD 2018世界人工智能峰会开场视频

困扰人类 159 年的最重要数学猜想被证明了？

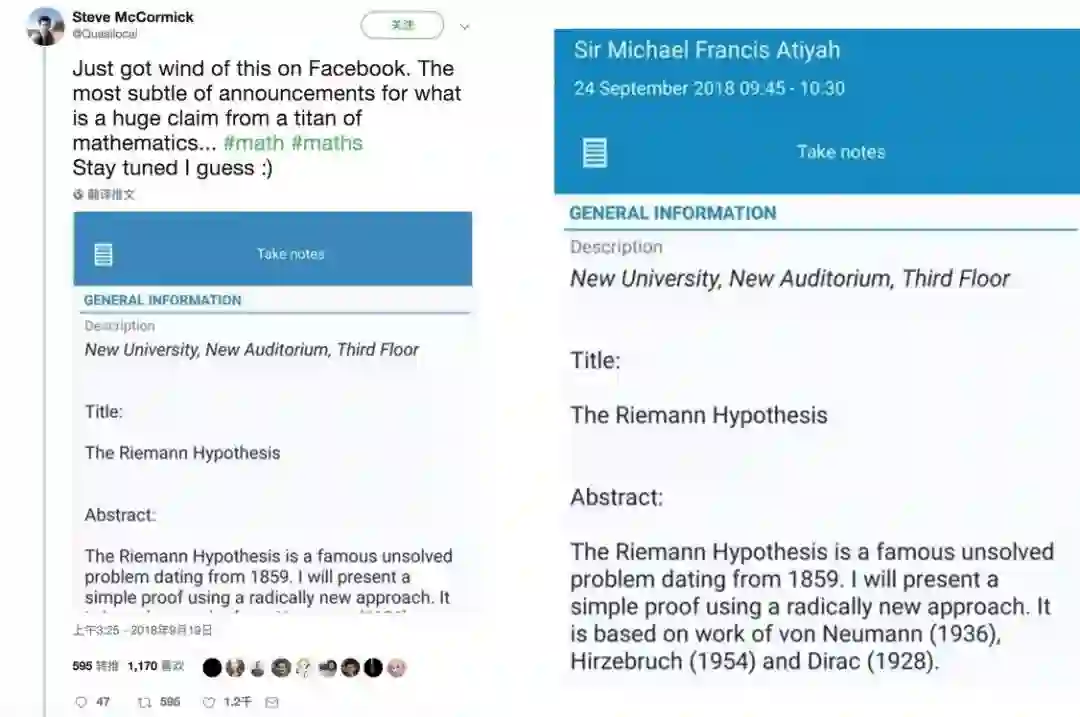
刚刚公布的德国海德堡获奖者论坛日程中，9 月 24 日著名数学家 Michael Atiyah 将会做一场关于 “证明黎曼猜想” 的报告。消息传出，数学物理计算机各路豪杰，纷纷炸了锅。

       

海德堡获奖者论坛官网的日程显示，该报告是在 9 月 24 日上午

网址：https://www.heidelberg-laureate-forum.org/event_2018/

瑞典籍澳大利亚数学家 Steve McCormick 在社交网络上发布了这一消息，引起大量关注，小编在论坛官网证实的确有这样一个日程。（论坛官网一直到今天下午才能访问，可能是全球数学爱好者听说消息纷纷赶来围观，服务器都被拖垮了）

       

       

翻译一下摘要：“黎曼猜想是 1859 年提出的著名问题，至今悬而未决。我会基于冯诺依曼（1936）、希策布鲁克（1954）和狄拉克（1928）的相关工作，给出一个使用全新方法的简洁证明。”

德国海德堡获奖者论坛（Heidelberg Laureate Forum）是一个由国际顶级奖项（图灵奖、阿贝尔奖、林奈奖、菲尔兹奖）得主与青年学者交流的研讨会，自 2013 年开始举办，顶尖学者每年齐聚一堂，相关讨论在数学届甚至整个科学界都受到广泛关注。在这样一个大场合，倒配得上公布黎曼猜想得证的消息。

黎曼猜想——最重要的数学猜想

早在 1737 年，大数学家欧拉就发现了质数分布问题与 Zeta 函数的联系，给出并证明了欧拉乘积公式，使得 Zeta 函数成为研究质数问题的经典方法。

       

欧拉乘积公式，其中 p 为质数，n 为自然数

黎曼猜想（Riemann Hypothesis）由大数学家黎曼在 1859 年首次提出，讨论黎曼 Zeta 函数的非平凡解问题。

黎曼猜想是众多尚未解决的最重要的数学问题之一，被克雷数学研究所列为待解决的七大千禧问题，悬赏百万美金证明或者证伪。一百年前希尔伯特就曾被问过一个问题 “假定你能死而复生，你会做什么？”，他的回答是，“我会问黎曼猜想是否已经解决”。可见黎曼猜想多么吸引人。

       

伯恩哈德 · 黎曼（Bernhard Riemann，1826-1866）

集智俱乐部在今年 5 月，曾经报道过研究者用晶体衍射实验研究质数分布问题的最新进展。质数分布间隔的规模至今是未解之谜，而研究者发现，如果用质数序列作为准晶体微粒的分布间隔，就可以在其光学衍射结果中发现出分形结构。这为解开质数之谜提供了新的灵感，但仍然不能直接证明黎曼猜想。

质数分布、分形几何、晶体衍射——竟然被一个小实验联系到一起

如何用 Mathematica  窥探质数分布中隐藏的分形规律

Michael Atiyah 爵士是何许人也，竟然有这样的野心？

数学最高奖获得者，Michael Atiyah 爵士

Michael Atiyah（1924-）是当代著名数学家，主要研究领是几何，他于 1966 年获得 4 年颁发一次的数学界最高奖菲尔兹奖，而且在 1990-1995 年担任英国皇家学会主席。

Michael Atiyah（1924-）

Atiyah 最重要的工作都是在上世纪六七十年代完成的。但作为一位年届九旬的科学家，他仍然活跃在学术前沿，并时常有惊人之举，2016 年他因为给出一个 “6 维球面上不存在复结构” 的证明被质疑而颇具争议。

而黎曼猜想本身的确非常难，所以在 Michael Atiyah 证明黎曼猜想的消息公开之后，社交媒体上多数人仍在观望，毕竟太多人都曾声称自己证明了黎曼猜想但之后却被推翻，连大数学家哈代也犯过这种错误。

难以证明又无法推翻的黎曼猜想

回到黎曼猜想上。黎曼猜想是关于黎曼 Zeta 函数的零点分布的猜想。黎曼 Zeta 函数长这个样子：

黎曼 Zeta 函数有两种零点，一种是位于实数轴线上的零点，被称为平凡零点，另一种是位于其他复平面区域上的零点，被称为非平凡零点，目前数学家已经证明这些非平凡零点全部位于实部区间为 0 到 1 的复平面内，而黎曼则大胆猜想，这些非平凡零点全部位于实部为 1/2 的一条直线上。

“所有非平凡零点都位于实部为 1/2 的直线上” 是一个尚未得到严格证明的猜想，但数学家们至今找到的上万亿个非平凡零点的确都位于这条直线上，无一例外。

视频《什么是黎曼猜想》

不止如此，黎曼猜想还跟幂律分布有关。

我们都知道幂律分布是指        

其中 x 如果只能取 1,2,3,...,n 的整数，c 为归一化常数，满足：

   

而这里面的        

就是 Zeta 函数，黎曼猜想就是关于这个函数的，但是 a 可以取复数值。

黎曼猜想真的会被证明吗？

质数分布没有简单规律，但质数出现的频率跟黎曼 Zeta 函数紧密相关。有数学家甚至认为黎曼猜想与强条件下的质数定理是等价的。目前已经验证了前 1,500,000,000 个质数对这个定理都成立，但至今没有完全证明。黎曼猜想得证，对质数研究、数论研究意义重大。

黎曼猜想对许多数学领域都意义重大，质数分布只是其中一个。有上千个数学命题都建立在黎曼猜想为真的基础上。多数数学家认为这个猜想是正确的，如果黎曼猜想被证伪，数学体系将失去重要根基。

作为菲尔兹奖和阿贝尔奖双料得主，Michael Atiyah 爵士已经功成名就，而且培养出许多优秀的年轻学者。如果真的证明了黎曼猜想，那 Michael Atiyah 就会登顶最伟大数学家的行列中。

真相如何？9 月 24 日见分晓！

关于黎曼猜想的推荐阅读：

1. 卢昌海 《漫谈黎曼猜想》 清华大学出版社
   

2. 德比希尔《素数之恋——黎曼和数学中最大的未解之谜》上海科技教育出版社

3. 视频 - 可视化黎曼 Zeta 函数和解析延拓

   https://www.youtube.com/watch?v=sD0NjbwqlYw&feature=youtu.be

编辑：集智小编

本文经授权转载自集智俱乐部，ID：swarma_org，点击阅读原文查看原文。

---

新智元AI WORLD 2018世界人工智能峰会

全程回顾

新智元于9月20日在北京国家会议中心举办AI WORLD 2018世界人工智能峰会，邀请机器学习教父、CMU教授 Tom Mitchell，迈克思·泰格马克，周志华，陶大程，陈怡然等AI领袖一起关注机器智能与人类命运。

全程回顾新智元 AI World 2018 世界人工智能峰会盛况： 

爱奇艺 

上午：https://www.iqiyi.com/v_19rr54cusk.html 

下午：https://www.iqiyi.com/v_19rr54hels.html

新浪：http://video.sina.com.cn/l/p/1724373.html