漫画 | 算法难题：海盗如何分金币？

本文经授权转载自「程序员小灰」

—————  第二天  —————

海盗分金币问题：

有5个海盗，获得了100枚金币，于是他们要商量一个方法来分配金币。商议方式如下：

1. 由5个海盗轮流提出分配方案。

2. 如果超过半数海盗（包括提出者）同意该方案，则按照该方案分配。

3. 如果同意该方案的人数（包括提出者）小于等于半数，则提出者要被扔到海里喂鱼，剩下的海盗继续商议分配。

4. 海盗们都是绝对理性的，以自己尽可能多获得金币为目的。但是在收益相等的情况下，会倾向把提出者扔到海里。

问：第一个海盗应该提出怎样的分配方案，才能保证自己既不被扔到海里，又能使自己利益最大化？

举一个栗子：

此时第一个海盗来提议分配方案，他说：

我要100枚金币，你们其他人一个金币也没有！

显然，其他小伙伴一致反对，结果第一个提出者被扔到了海里。

接下来轮到第二个海盗提出分配方案，他说：

我只要1个金币，剩下3个小伙伴每人33个金币！

第三个海盗反对，剩下两个小伙伴同意，同意者超过了半数（4 : 1），于是按照这个方法执行了分配。

————————————

如何利用递归思想来简化问题呢？让我们来详细分析一下，后文把五个海盗简称为老一、老二、老三、老四、老五。

老一在提出分配方案的时候，不妨这样思考：

如果我被扔到海里了，剩下4个海盗，此时老二的最优分配方案是什么呢？

我只要在老二的分配方案上稍微增加一点，就能赢得更多的支持。

老二在提出分配方案的时候，也会这样思考：

如果我被扔到海里了，剩下3个海盗，此时老三的最优分配方案是什么呢？

我只要在老三的分配方案上稍微增加一点，就能赢得更多的支持。

老三在提出分配方案的时候，还是会这样思考：

如果我被扔到海里了，剩下2个海盗，此时老四的最优分配方案是什么呢？

我只要在老四的分配方案上稍微增加一点，就能赢得更多的支持。

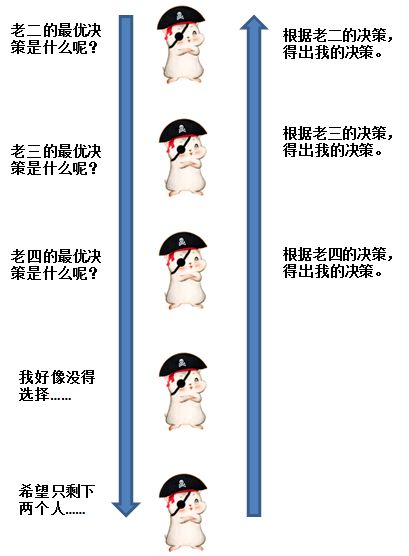
整个递归过程，就像下图一样：

这个递归过程到什么时候截止呢？剩下两个人为止。

想想看，当剩下两个人的时候，是什么情形？

此时老四没有任何选择！无论他如何分配，哪怕把100枚金币都给老五，老五仍然可以反对，导致老四被扔到海里，金币全归老五所有。

由此，老三心想：老四没有最优决策，所以无论我提出什么要求，老四都一定会同意，而老五一定不同意。

由于只要超过半数同意就可以执行分配，所以老三的最优策略如下：

接下来，老二暗自寻思：如果没有我，老三能获得100枚金币，所以无论如何不会同意我。但我可以设法“笼络”老四和老五，形成 3 : 1 的局面。

在老三的“淫威”下，他们原本一个金币都得不到。我给他们一人一枚金币，好过由老三来分配，所以他们肯定会同意。

因此，老二的最优策略如下：

终于轮到老一了，老一心里琢磨：如果没有我，老二能获得98枚金币，我总不能分给他多于98枚，索性放弃他，只要剩下三人中笼络到两人，形成 3 : 2 的局面即可。

要笼络谁呢？以老二的策略，老三得不到金币，所以老三最好“伺候”。我给老三1枚，老三一定同意。

至于老四和老五，本来可以得到1枚，所以我必须比老二给的多，才能赢得支持。但我又没必要同时笼络他俩，要么给老四两枚金币，放弃老五，要么给老五两枚金币，放弃老四。

因此，老一的最优策略如下：

作者简介：程序员小灰，帝都工程师一枚，先后在京东、摩拜任职。

 热 文 推 荐 

☞互联网寒冬下，为什么就你被裁了？

☞吃亏的程序员，是如何拿到了9个月的年终奖？

☞程序员有话说 | 程序猿在乘地铁的时候都在想什么?

☞边缘计算精华问答 | 为什么需要边缘计算？

☞心疼！能为程序员男友做些什么吗？

☞以太坊升级的拖油瓶，竟只是这几行代码

☞2019年人工智能行业又进入冬天了吗？

☞谁能真正“撬动”微信？| 畅言

print_r('点个好看吧！');
var_dump('点个好看吧！');
NSLog(@"点个好看吧！");
System.out.println("点个好看吧！");
console.log("点个好看吧！");
print("点个好看吧！");
printf("点个好看吧！");
cout << "点个好看吧！" << endl;
Console.WriteLine("点个好看吧！");
fmt.Println("点个好看吧！");
Response.Write("点个好看吧！");
alert("点个好看吧！")
echo "点个好看吧！"

点击“阅读原文”，打开 CSDN App 阅读更贴心！

喜欢就点击“好看”吧