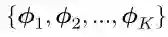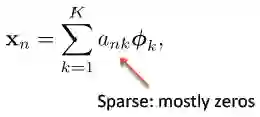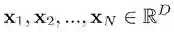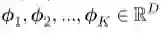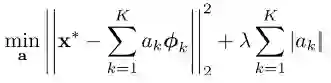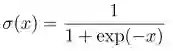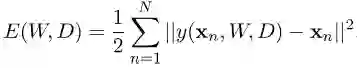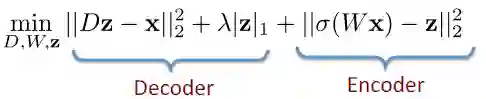教程 | 无监督学习中的两个非概率模型:稀疏编码与自编码器
机器之心整理
作者:Ruslan Salakhutdinov
参与:Smith
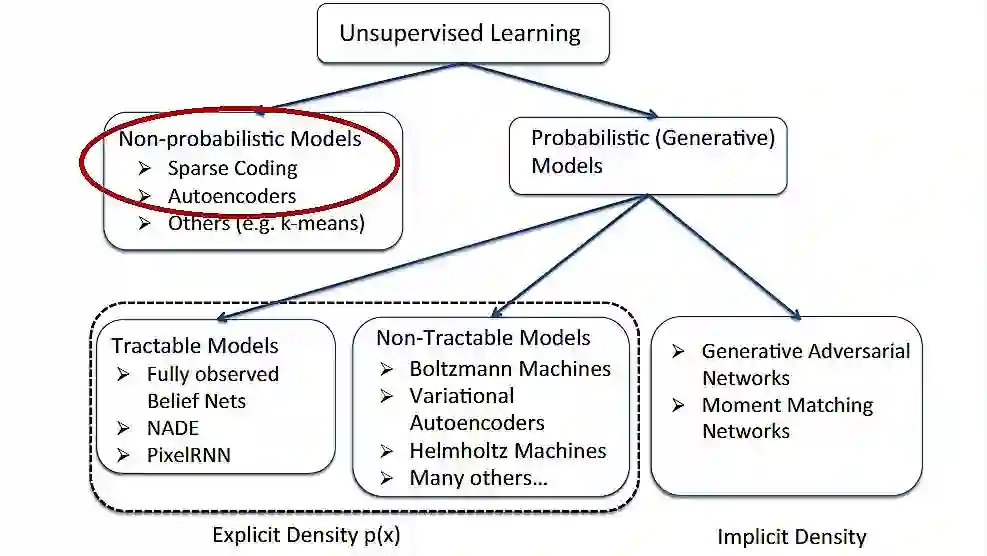
「无监督学习」(Unsupervised Learning)现在已经成为深度学习领域的热点。和「有监督学习」相比,这种方法的最大优势就在于其无须给系统进行明确的标注(label)也能够进行学习。最近,在德国的图宾根,机器学习夏训营(Machine Learning Summer School)正在如火如荼地进行,其中来自 CMU 的 Ruslan Salakhutdinov 教授就带来了很多关于「无监督学习」的精彩内容。今天机器之心给大家分享的正是其课件中有关「无监督学习中的非概率模型」的相关内容,主要介绍了稀疏编码(Sparse Coding)和自编码器(Autoencoder),这两种结构也是「无监督学习」的基本构件。完整课件可查看「阅读原文」PDF。
一、稀疏编码(Sparse Coding)
1. 稀疏编码的概念
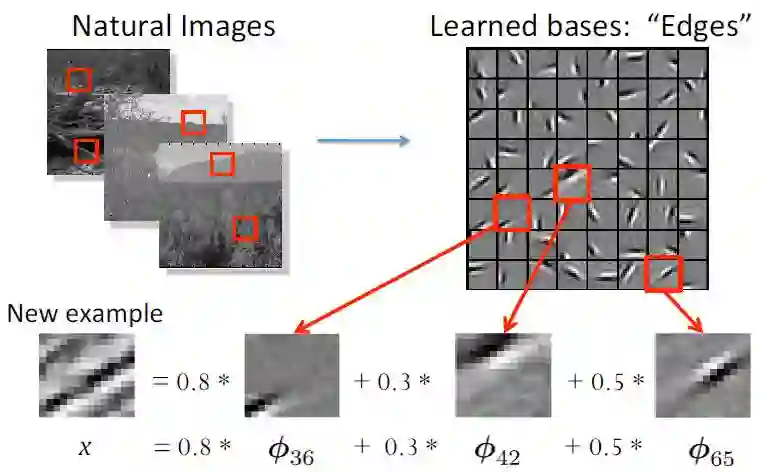
稀疏编码最早由 Olshausen 和 Field 于 1996 年提出,用于解释大脑中的初期视觉处理(比如边缘检测)。
目标:给定一组输入数据向量 { x1,x2,...,xN },去学习一组基字典(dictionary of bases):
满足:
其中 ank 的值大部分都为 0,所以称为「稀疏」。每一个数据向量都由稀疏线性权值与基的组合形式来表达。
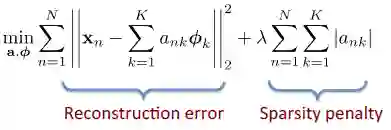
2. 稀疏编码的训练
为输入图像片段;
为要学习的基字典(dictionary of bases)。
这个表达式的第一项为重构误差项;第二项为稀疏惩罚项。
交替性优化:
1. 固定基字典,求解激活值 a(这是一个标准的 Lasso 问题);
2. 固定激活值 a,优化基字典(凸二次规划问题——convex QP problem)。
3. 稀疏编码的测试过程
输入为一个新图像片段 x* , 和 K 个可学习的基;
输出为一个图像片段 x* 的稀疏表达 a(sparse representation)。
[0, 0, ..., 0.8, ..., 0.3 ..., 0.5, ...] 为系数矩阵,也叫做特征表示(feature representation)。
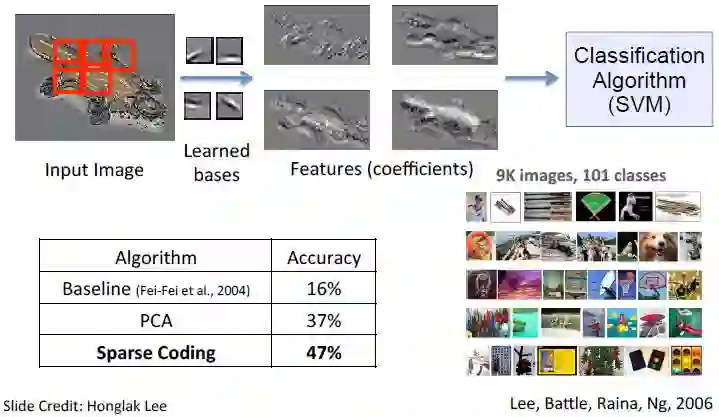
下图为应用稀疏编码进行图像分类的相关实验结果,该实验是在 Caltech101 物体类别数据集中完成的,并且用经典的 SVM 作为分类算法。
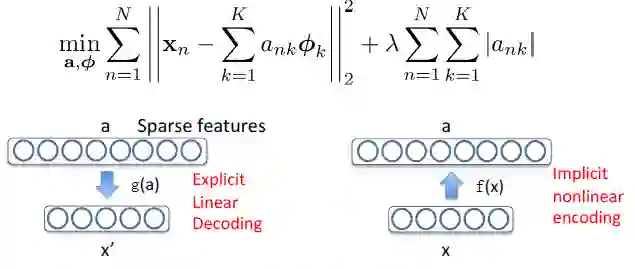
4. 稀疏编码的相关解释
a 是稀疏,且过完备(over-complete)的表征;
编码函数 a = f(x) 是 x 的隐函数和非线性函数;
而重构(解码)函数 x' = g(a) 是线性且显性的。
二、自编码器(Autoencoder)
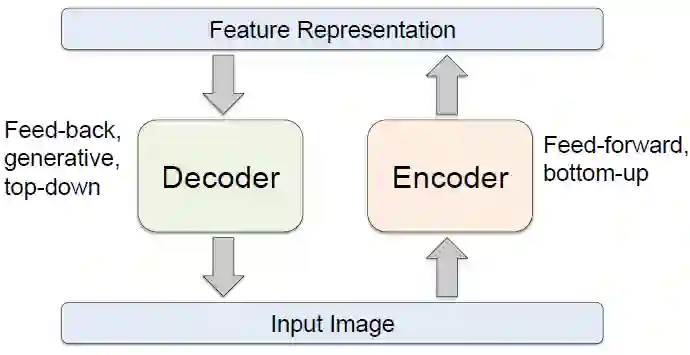
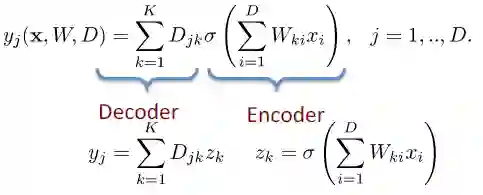
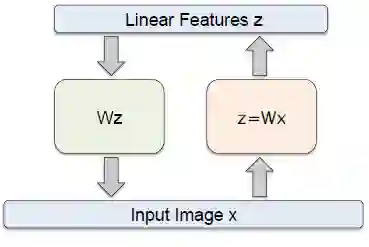
1. 自编码器结构
编码器和解码器内部的详细数据信息至关重要;
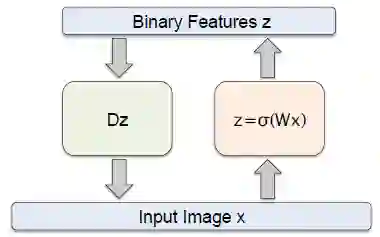
2. 自编码器范例
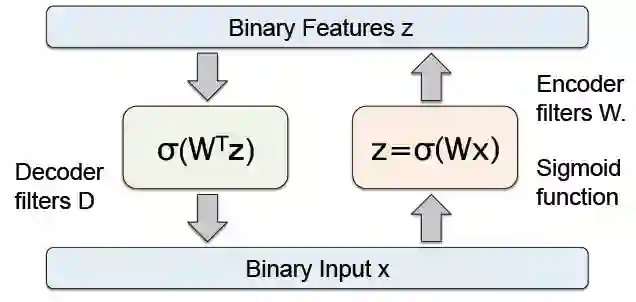
如上图所示,编码器的过滤器(filters)为 W,函数为 Sigmoid 函数,
解码器的过滤器(filters)为 D , 函数为线性回归函数。
这是一个拥有 D 个输入和 D 个输出的自编码器,并且包括 K 个隐单元(hidden units), K<D。给定输入 x,它的重构函数为:
我们可以通过使重构误差(reconstruction error)最小化来决定网络的参数 W 和 D :
3. 其它自编码模型
如果隐蔽层(hidden layer)和输出层是线性的,它将会对隐单元(hidden units)进行学习,这些隐单元是数据的线性方程,并且可以使方差最小化。这 K 个隐单元将会像前 K 个主成分(first k principal components)一样,覆盖相同的空间。这些权重矢量可能不是正交的。
对于非线性隐单元的情况来说,我们会利用 PCA(Principal Component Analysis)的非线性泛化(nonlinear generalization)来进行处理。
和限制性玻尔兹曼机(Restricted Boltzmann Machines)相关。
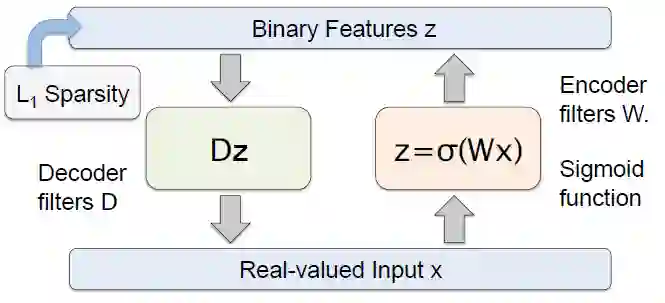
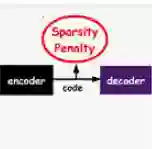
预测稀疏分解(Predictive Sparse Decomposition):
在训练过程中:
可以看到,这种结构在解码器部分加入了稀疏惩罚项(详见以上关于稀疏编码的内容)。
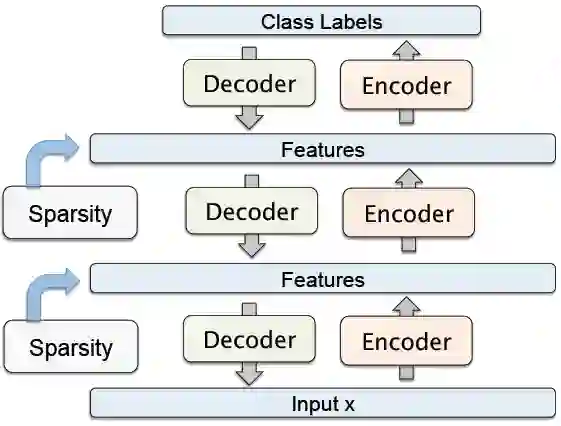
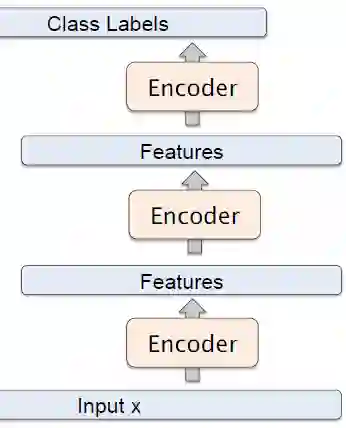
4. 堆叠式自编码器(Stacked Autoencoder)
这是一种「贪婪」的分层学习。如果我们去掉解码器部分,并且只使用前馈部分,会发现这是一个标准的类似于卷积神经网络的结构,参考下图。可以使用反向传播来对参数进行调校。
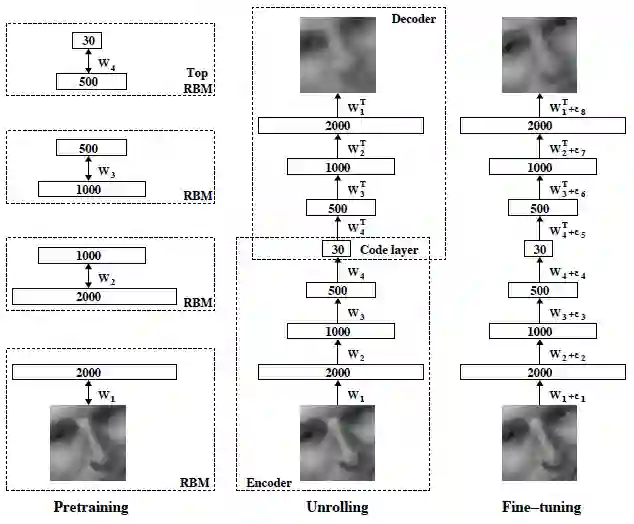
5. 深度自编码器结构及其相关实验结果
第一行:从测试数据集中随机采样;
第二行:用 30 维的自编码器进行重构得到的结果;
第三行:用 30 维的 PCA 进行重构得到的结果。
本文为机器之心原创,转载请联系本公众号获得授权。
✄------------------------------------------------
加入机器之心(全职记者/实习生):hr@jiqizhixin.com
投稿或寻求报道:editor@jiqizhixin.com
广告&商务合作:bd@jiqizhixin.com