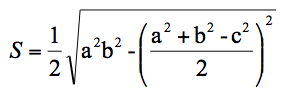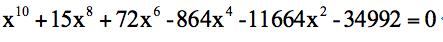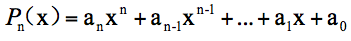谜一般的流星

2018 年 3 月 23 日 算法与数学之美 王雁斌

本文节选自广西师大出版社《数学现场：另类世界史》！

李冶在钧州率领金国将士血战蒙古骑兵的时候，一个二十四岁的年轻人正在南宋的临安过着逍遥自在的日子。他刚刚考上了进士，踌躇满志地筹划自己的仕途，并特意为自己取了一个号，叫作道古（效法古人行事的意思）。这个无比聪明的年轻人在当时人们的眼里，前途确实无可限量。但后来的事实证明，他的仕途并不顺利，而且留下很糟糕的名声。

道古出生在四川，父亲曾在巴州为官。后父亲因战乱带领全家迁至首都临安（今天的杭州）。几年工夫，父亲擢升工部郎中、秘书少监兼国史院编修官、实录院检讨官。由于父亲是掌管各项工程、屯田、水利、交通的工部郎中，又任国史院官职，掌管各类经籍图书，使道古得以接触学习各类知识。他的生性一定非同寻常的聪颖，因为很快他就对当时的种种学问，如星象、音乐、算术以及建筑学等无一不通。更重要的是，他还曾经向当时的隐士求教，学习数学。

他十八岁就当上了住地的义兵首，后到郪县（今天的四川绵阳附近）做县尉。有了进士身份以后，他更是仕途大展。几年内，他从湖北蕲州（今湖北蕲春县）通判擢升为和州（今安徽和县）知州，又赴建康府（今江苏南京）为官。眼见一切顺利，可就在这时，他的母亲去世了。按照规矩，凡是丧父丧母的官员必须解职守孝三至五年，这叫作丁忧。道古急赴临安吊丧，然后转回湖州老家。

13世纪上半叶，南宋小朝廷是在喜忧参半的心情下度过的。蒙古的崛起给南宋带来了极大的威胁，而金国又不断地骚扰，两国征战不绝。公元1234年，为了一雪北宋灭亡的靖康之耻，南宋朝廷派使者前往蒙古，双方结成联盟，共同对付金国。作为宋军援战的报酬，蒙古承诺灭金后把黄河以南的中原地带归还南宋。不久，蒙宋联军攻入金国首都汴梁，金哀宗完颜守绪（公元1198—公元1234）自缢身亡。指挥南宋盟军的大将孟珙（公元1195—公元1246）把金哀宗的尸骨带回临安，举国一片欢腾，人们竞相庆贺，一百年的耻辱终于以金国的灭亡而告终。可是金被灭以后，南宋的西部和北部直接暴露在蒙古的威胁面前。窝阔台可汗灭金后，立即撕毁了将黄河以南归还南宋的协议，强迫改为陈州、蔡州以北属蒙古，以南属南宋。这使南宋失去了黄河与长江之间的大片肥沃土地，也失去了黄河的屏障。南宋政府无力反抗，只能忍辱接受。从此，南宋的忧患越来越严重，蒙古骚扰不断，国无宁日。

按当时的规矩，丧母的道古不能从政，在湖州过了四五年平静的日子。我们不知道他都做了些什么，因为史书上没有记载。但是在宋理宗淳祐七年（公元1247年）的秋天，他突然刊出一本书来，名叫《数学大略》。书的前面有《序》一篇，对自己著书的经历有这样的描述：“时际兵难，历岁遥塞，不自意全。于矢石之间，更险离忧，荏苒十祀。”大意是说，在兵荒马乱的年代，交通不便，所以无法写得详细全面。这本书是在石雹箭雨当中写成的，期间充满了忧愁和艰险，又经过十年的修改才完成。这一年，道古三十九岁。也就是说，他是从二十九岁起就开始写这本书了。

这本书就是后来的《数书九章》，它在世界数学史上占有非常重要的位置。道古，大名秦九韶（公元1208—公元1261），也因此被称为中国历史上最伟大的数学家。

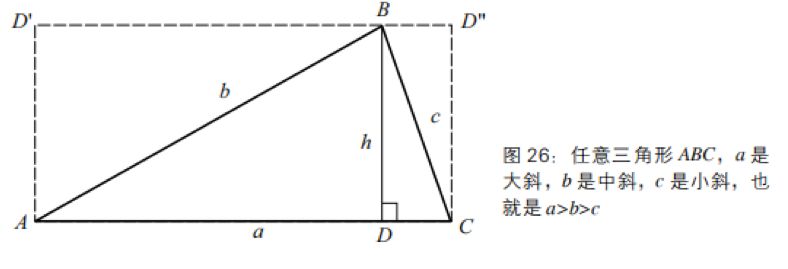
在这本书里，秦九韶有三项最重要的数学贡献。第一个贡献是所谓的秦九韶公式。《数书九章》第五卷有“三斜求积”一题。其中“三斜”为“大斜”“中斜”“小斜”，是三角形从大到小的三条边（图26）。秦九韶列出的任意三角形面积S的公式，用现在的代数语言表达是：

这个公式的基本出发点是出入相补（又称以盈补虚）原理，它是中国数学中用于推证几何图形的面积或体积的基本原理。其内容如下：

1.一个几何图形，可以切割成任意多块任何形状的小图形，总面积或体积维持不变——所有小图形面积或体积之和。

2.一个几何图形，可以任意旋转、倒置、移动、复制，面积或体积不变。

3.多个几何图形，可以任意拼合，总面积或总体积不变。

4.几何图形与其复制图形拼合，总面积或总体积加倍。

出入相补原理是三国时代的数学家刘徽创建的。他说：“勾股各自乘，并而开方之，即弦。”这就是直角三角形的勾股定理。然后他又说：“勾自乘为朱方，股自乘为青方，另出入相补，各从其类，因就其余不移动也，合成弦方之幂，开方除之，即弦也。”

从图26，刘徽从B点作线段AC的垂线，交AC于点D，得到两个直角三角形ADB和BDC，它们的高相同，都是BD=h。现在复制三角形ABD，把它旋转180度，使得复制后的三角形和ABD的斜边重合，也就是图26中的三角形ABD′。由于这两个三角形都是直角三角形，它们的和是一个矩形ADBD′。同样复制直角三角形BDC，得到三角形BD″C，和矩形DCD″B。两个矩形的总和ACD″D′，其面积从古巴比伦和古埃及时代就知道了，是a×h；所以，三角形ABC的面积是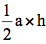。把复杂的几何形状转换为简单形状，然后求解，这其实跟海亚姆的“填充方块法”的思路是很类似的。秦九韶从这里导出用边长来表达的面积公式，具体做法，我们留给读者吧。

在欧洲，这个公式在希腊化时期就被亚历山大里亚的希罗（Hero of Alexandria，约公元10—公元70）明确地证明了，只不过表达方式不同。比希罗早两个世纪的阿基米德很可能就已经得到了这个结果。在中国，是秦九韶发现了这个公式。这是一个很重要的公式，因为任何一个n（n>3）边多边形都可以切割成n-2个三角形。有了这个公式，可以很容易地计算出任何n边多边形的面积。

秦九韶的第二个贡献是求解一元高次方程的数值解。秦九韶找到了一个通用解法，可以用于任何阶次的一元方程。在“遥测圆城”的题目下面，他利用筹算，求得一个一元十次方程的正数解。这个问题也同战争有关：在无法接近敌人城池的情况下，如何根据测量来计算城池的大小？假定城墙是圆环状的，秦九韶得到这样一个方程：

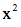
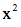
其中是需要求得的城池的直径。秦九韶没有做=y之类的变量代换，而是直接摆开算筹来求这个方程的数值解，因为他有一套系统的求解方法。利用他的方法，可以很快求得x=3，因此圆城的直径是九里。他的方法已经跟现在应用数学中的计算程序非常接近，只不过是需要人来移动摆放算筹罢了。这个方法现在被称为秦九韶算法。

秦九韶的方法让后世的数学史专家们惊诧不已，因为它采用了五六百年以后才为人们所认识的数学原理和算法。跟他的前辈——中国和古埃及数学家一样，他拿起就用，不加证明。他对这些知识的熟悉程度是不言自明的。

首先是多项式余式定理：把任意一个n>1的多项式

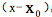
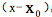
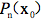
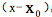
。除以，所得的余数等于该多项式在时的值。其次是综合除法的算法，也就是如何对任意多项式做除以的实际操作。

为了简单起见，我们只看三次多项式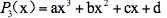。我们想把这个多项式除以（x-g），应该怎么做呢？见下面图27：

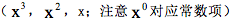
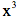
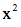
先在第一行列出x的各个幂位。在该行的左面画一条竖杠，把（x-g）中的数字g写在竖杠的左面，准备用它来做计算。把多项式x各个幂位的系数写在相应幂位的下方，作为第二行。留出一个空行（第三行），在第三行的下面画一条横杠。用g乘以第二行的第一个系数，也就是的系数a，得到ag，把它写在第三行对应那一列的位置。对该列第二行、第三行的数字（b和ag）做加法，把结果（b+ag）写在第四行该列的位置。下一步把这个结果（b+ag）乘上g，写到第三行第三列（对应那一列），对该列第二行、第三行两数做加法，得到c+[g(b+ag)]，把它写在第三列第四行的位置上。对第四列重复以上步骤，最终得到图27的结果。

为什么要这么做？请读者自己验证下面的等式：

（14）

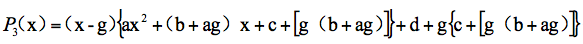
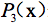
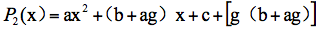
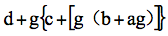
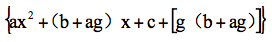
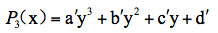
这个等式说明，通过图27的步骤，我们已经把变成（x-g）和一个二次多项式的积再加上余式（或余数）。事实上，对第四行左面的三项所给出的二次多项式，还可以再除以（x-g）。得到的单次项还可以再除以（x-g）。这样，最终可以把（14）变成另一种表达方式：

（14a）

这里，y=x-g，带撇的系数是相应变化后的系数。

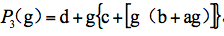
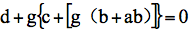
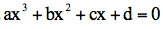
现在使用余式定理。根据这个定理，在x=g时，。所以，如果找到g，使，我们就找到了方程的一个解。这样，我们对求解高阶方程有了一个出发点：把n阶方程看作n阶多项式，猜测一个近似解x=g，将n阶多项式化简为（x-g）乘以一个n-1阶多项式，使余数接近于零。如果第一个猜测解的余数大于零，试另外一个猜测解，直到找到一个猜测解，其余数小于零。有了最接近于零的两个猜测解，一个余数大于零，另一个余数小于零，方程的根就在这两个猜测解之间。

举个例子。考虑如下方程：

（15）

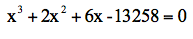
常数项是13258，我们需要猜测一个近似解，使其三次方接近这个

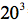
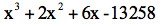
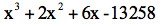
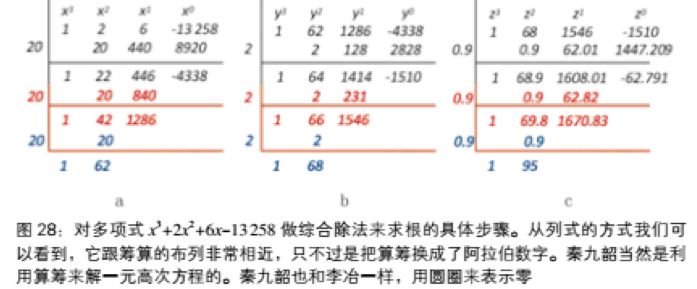
数。粗略的猜测是一个介于20和30之间的数，因为，=8000，小于13258，=27000，大于13258。把这两个猜测解代到方程（15）里，我们发现当x=20时，<0，当x=30时，>0。于是我们肯定真正的解在这两个值之间。现在我们按照图27的步骤把上面的方程除以（x-20）=y（图28a）：

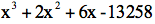
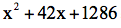
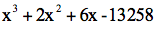
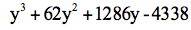
注意图28a中，我们对以y=x-20连续做了三次除法，第一次除法跟图27完全一样，得到的最后一行黑色数字的前三项对应的是一个二项多项式，余数为-4338。红色的数字是把这个二项式除以y=x-20，得到的是单项式x+42，余数为1286。蓝色的数字是把x+42再除以y，得到余数62。这是什么意思呢？读者不妨自己验证一下，我们通过以上步骤，把原来的多项式变成了，这里y=x-20。

我们已经知道x的根在20和30之间，所以现在要求的y的根一定是一个个位数。试一下y=5，发现余数是个很大的正数8105。再试y=4和3，余数都是正数。图28b是y=2的多项式除法，余数从y=3的正数变成负数。这样，我们得到（15）的近似到个位的解x=22。

当然还可以继续做下去。图28c是在做了另一个变换z=y-2以后，选择z=0.9的多项式除法。现在余数已经是很小的负数了。如果觉得x=22.9还不够精确，那就继续做下去。请读者验证，下一个数位的数值是0.03。

这个方法也很像计算机的程序，可以一直运算下去，直到达到满意的精度为止。更重要的是，它对方程的阶次没有限制。秦九韶解过一元10次方程，而实际上任何阶次的方程它都能解。唯一的缺点是它给不出普遍的公式，只能提供数值解。他还给这个方法取了个漂亮的名字，叫玲珑开方术。

在欧洲，这个绝妙的计算方法要到五百多年后的19世纪上半叶才由英国数学家威廉·乔治·霍纳（William George Horner，公元1786—公元1837）提出来。数学家奥古斯都·德·摩根（Augustus De Morgan，公元1806—公元1871）曾经对霍纳的方法赞叹不已，说它“必使其发明人因发现此算法而置身于重要发明家之列”。但是不久，英国传教士伟烈亚力（Alexander Wylie，公元1815─公元1887）就对霍纳的发明权提出了质疑。他在公元1852年所著的《中国数学科学札记》中，详细介绍了秦九韶的玲珑开方术之后写道：“读者不难认出这就是霍纳在1819年发表的《求解所有次方程》论文中的结果……我以为应该对霍纳的发明权提出辩驳。欧洲的朋友们可能会觉得意外，一位来自天朝帝国的竞争者有更大的机会确立他的优先权。”

秦九韶的第三大贡献是对《孙子算经》里“有物不知其数”的余数问题做出了全面系统的回答，找到了解决同余式组的一般方法，他称之为“大衍求一法”。这个方法现在成为中国余数定理。这个问题超出了我们的故事范围，只要引用下面这个评价，就可以知道它对后来数论的影响有多大了：

“秦的工作是如此的精妙，我们很想知道他是如何得到这样的成就的……他不可能是从印度人那里学到处理这类问题的方法的，因为他的方法和印度人的差异很大。结论是，我们必须承认，秦是从古至今所有数学家当中的一位伟人……秦自称是在杭州皇家机构学习天文时从计算历书的专家们那里学来的。不过他又说，那些专家只知道按照规则计算，却不知道为什么。这是可信的，天文历书的计算确实需要一些同余的基本理论。秦把当时的理论向前推进了巨大的一步，并且表现出难得的谦虚——这种谦虚在他生活的其他方面是相当缺乏的。他的工作到底有多精彩？只要提到下面几个事实就够了：欧拉（Leonhard Euler，公元1707—公元1783）未能为这个理论提供令人满意的证明；秦的方法需要等到高斯（CarlFriedrich Gauss，公元1777—公元1855）等人出现后才被重新发现。”

（参见苏格兰圣安德鲁大学“数学小家教”网站http：//www-history.mcs.st-andrews.ac.uk/Biographies/Qin_Jiushao.html）

数海拾贝

如果两个整数除以同一个正整数得到相同的余数，那么这两个整数就成为同余。这是数论里面一个重要的等阶关系。最早的同余问题出现在《孙子算经》里：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？答曰：二十三。

这是一个一次同余式组：

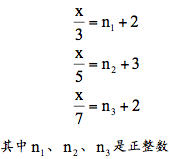
《孙子算经》成书的时间目前还不大清楚。估计是在魏晋或南北朝期间（4世纪——6世纪）。

秦九韶的《数书九章》和李冶的《测圆海镜》几乎是同时出版的。那时李冶已年近花甲，而秦九韶正值而立之年，应该说前途远大。非常遗憾的是，才华横溢的秦九韶从那以后再也没有任何建树。《宋史》当中没有关于他的记载，我们只能在宋人笔记和一些地区文献中发现他的踪影。跟他同时代的诗人刘克庄（公元1187—公元1269）说他“暴如虎狼，毒如蛇蝎”。比他小二十几岁的周密在《癸辛杂识》里对他除了“性极机巧，星象、音律、算术，以至营造等事，无不精究”“骈俪、诗词、游戏、球马、弓箭，莫不能知”，没有好话。根据周密的描述，秦九韶似乎是一个性格暴烈、为所欲为、报复心理极强的人。他绝不是那种温文柔弱，低声细语的学者。所以上面的评论说谦虚在他生活的其他方面是非常缺乏的。

根据周密的记载，我们还知道，秦九韶浸淫在腐败的南宋官场而不能自拔，把精力都放在讨好重臣如贾似道、吴潜等人之上。贾似道是当时公认的奸臣，宋人和元人都认为贾似道对南宋的灭亡负有不可推诿的责任。吴潜在任期间，同贾似道政见不合，二人经常在皇帝面前互说坏话，每个人周围都有自己的支持者。而秦九韶则在两面游移摇摆，见风使舵，让当时的士人很瞧不起。更不堪的是他贪财，捞起钱来不择手段。从二十几岁当官开始，他的名声就很坏。贾似道给了他一个琼州的官职，上任才几个月，他就捞得盆满钵满，归来时“所携甚富”。对于他不喜欢的人，他可以动用毒药，欲置之于死地。如此等等，罄竹难书。但是周密在这些颇为详细的记载之后又加了一句“陈圣观云”（听陈圣观说的），可见周密所记述的事情也可能只是道听途说。

清朝同治年间，湖州藏书家陆心源（公元1834—公元1894）负责编修《湖州府志》，根据刘克庄和周密的记载，决定不把秦九韶录在“湖州寓贤”之内。这非常可惜，由于陆心源的一己之见，关于秦九韶生平的宝贵资料就永远遗失了。今天有人试图为秦九韶洗清污名，但信实可靠的资料非常少。

同治八年上元，宗湘文源翰（注：宗源翰，字湘文，文学家）权知湖州，邀余及汪谢城（注：汪日桢，号谢城，清代天文学家）、广文丁宝书处士同修《湖州府志》，以三年之久。谢城仅认“蚕桑”一门，馀皆余与宝书任之。及《府志》成，郡人议修县志，谢城籍录乌程，随以《乌程志》属之。其各传皆取材于《府志》，而于“宋寓贤”增《秦九韶传》。考九韶之为人，有不孝、不义、不仁、不廉之目。先有议幕之除，首遭驳论，又除农丞，措置平江米餫，后省再驳，其命遂寝。后村谓其人暴如虎狼，毒如蛇蝎，非复人类……周密与九韶同寓湖州，或有乡里私怨，后村（注：后村是刘克庄的字）气节文章名重当世，且见之奏驳，必非无影响者。故余修《府志》，于《寓贤》不为立传，而谢城矜为独得，不免变乱是非矣。

陆心源《同治乌程县志跋二》

本文节选自广西师大出版社《数学现场：另类世界史》，作者：王雁斌