Google面试题 | 不包含连续1的非负整数

作者 | 施助教 & ben 助教

编辑 | Ivy Xu

专栏 | 九章算法

题目描述

给定一个正整数n，求出0到n中有几个数满足其二进制表示不包含连续的1。1<=n<=10^9。

样例

输入：5

输出：5

说明：0到5的二进制表示分别为：

0 ： 0

1 ： 1
2 ： 10
3 ： 11
4 ： 100
5 ： 101

这六个数中，只有3的二进制表示包含有连续的1，故答案为5。

解题思路分析

暴力方法：枚举0到n，判断其二进制是否包含连续的1，时间复杂度为O(n*log(n))，对于题目的n的范围来说比较大。

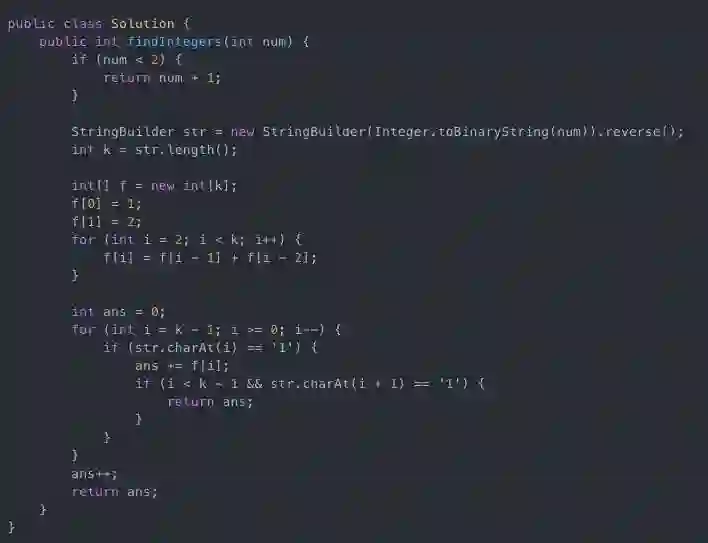
考虑一种比较简单的情况，如果n=2^k - 1，其中k为正整数，那么问题就变成二进制数00……0（k个0）到11……1（k个1）中有几个数不包含连续的1，设答案为f(k)。

我们可以考虑k位二进制数的第一位：如果第一位是0，那么第二位既可以取0也可以取1，也就是说对后面的k-1位无影响，所以第一位为0的满足条件的数总共有f(k-1)个；如果第一位是1，那么由于不能出现连续的1，第二位只能取0，但是对后面的k-2位无影响，所以第一位为1的满足条件的数总共有f(k-2)个。

这样，我们就得到了：f(k) = f(k-1) + f(k-2)。边界条件为f(1)=2以及f(2)=3，由于f(0)=1满足原问题的题意也满足上述的转移方程，故可以取边界条件f(0)=1，f(1)=2。

对于n不是2^k-1的一般情况，与上一点的不同之处在于：上一点中只要满足二进制位长度不超过k，那么这个数就不会超过n=2^k - 1，而这种情况需要具体考虑不超过n的数。

假设n的二进制有k位，最高位为1，其二进制为1xx……x（x表示0或1），那么0到n可分为00……0（k个0）到011……1（一个0，k-1个1）和100……0（一个1，k-1个0）到1xx……x（即n）两个部分。

前一个部分即0到2^(k-1)-1，这部分中满足条件的答案为f(k-1)；第二部分则需进一步讨论：如果n的二进制从左往右第二位为1，即n的形式为11x……x，那么因为题目要求不能有连续的1，所以这一位只能取0，这样的数一定小于n，所以后k-2位不受大小的限制，答案为f(k-2)，并结束计算；如果n的二进制从左往右第二位为0，即n的形式为10x……x，那么为满足不超过n的条件，第二位也只能取0，这样问题就变为从100……0到10x……x之间有多少满足条件的数，这样就可以继续对n的二进制的后k-2位进一步进行类似的讨论。

举个例子，n=10，二进制为1010：

对于最高位的1，我们将0到1010分为0到111和1000到1010两部分，前一部分的个数为f(3) = 5。

第二部分为1000到1010，最高位确定取1，而n的二进制从左往右第二位为0，为满足不超过n的条件，满足条件的数从左往右第二位只能取0。

n的二进制从左往右第三位为1，这样我们又可以按i中的方法，把1000到1010再次分成1000到1001和1010两个部分，前一部分的个数为f(1) = 2。

到n的最低位，为0，故最后一位只能取0，按照之前的算法这一步不会增加答案，但由于n=1010b本身还没有计入，故再加1。

最后得到答案5+2+1=8。

n的二进制长度为log(n)，故该算法的时间复杂度为O(log(n))。

参考程序

http://www.jiuzhang.com/solution/non-negative-integers-without-consecutive-ones/

面试官角度分析

这道题考察位运算的基本知识和动态规划的思想，难点在于如何原本的逐个统计问题通过二进制分类统计，属于面试中中等难度的题目。给出正确的解法可以达到hire。

lintcode相关问题

http://www.lintcode.com/zh-cn/problem/counting-bits/

九章算法班 | 硅谷求职必修课

面试中的常见误区

从面试官的角度分析面试的考察点

从Subset中了解算法面试中模板的重要性

正在报名中！

报名登陆官网 www.jiuzhang.com

或点击文末“阅读原文”