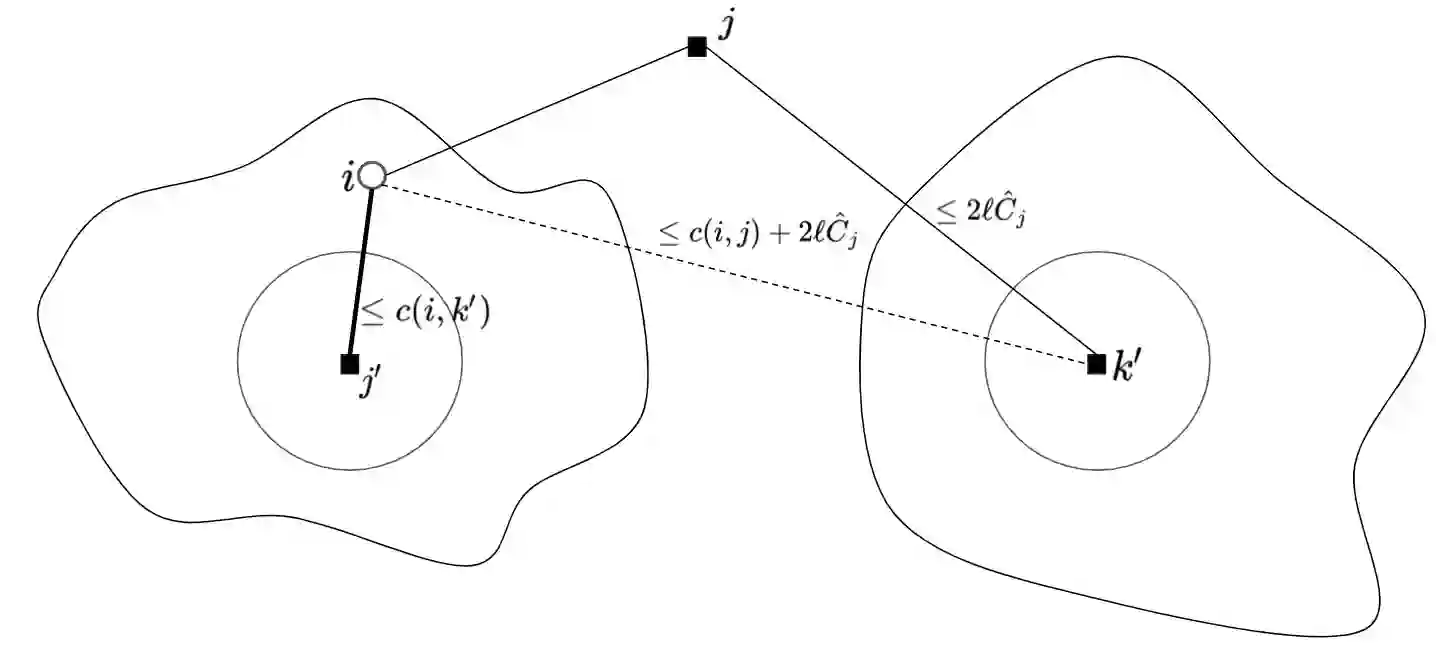
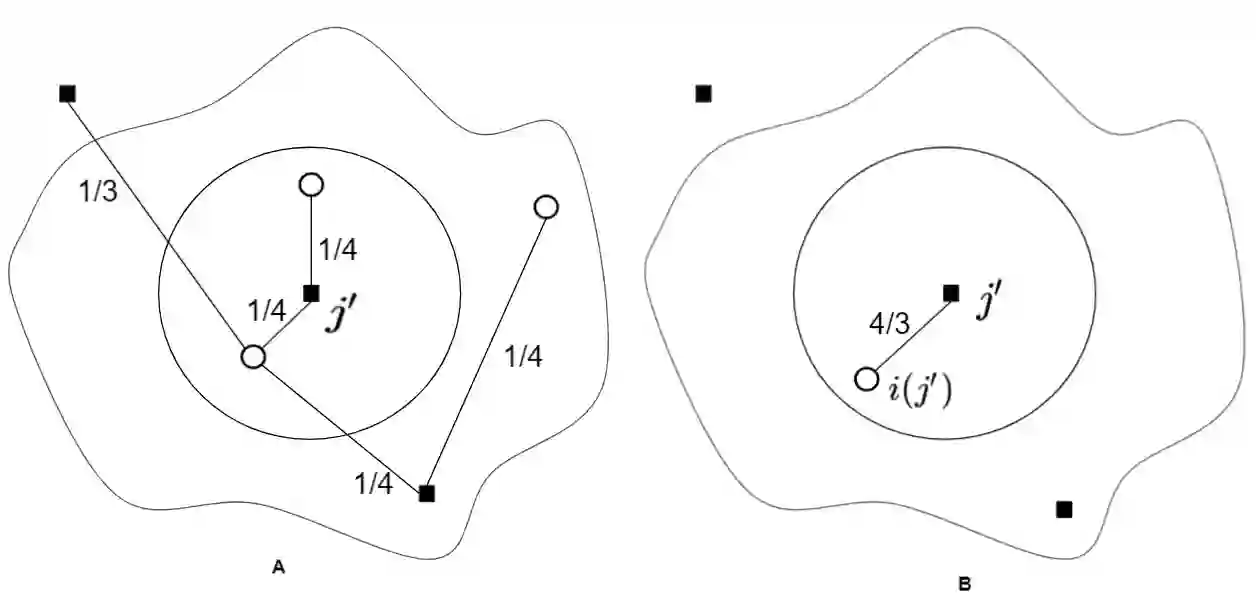
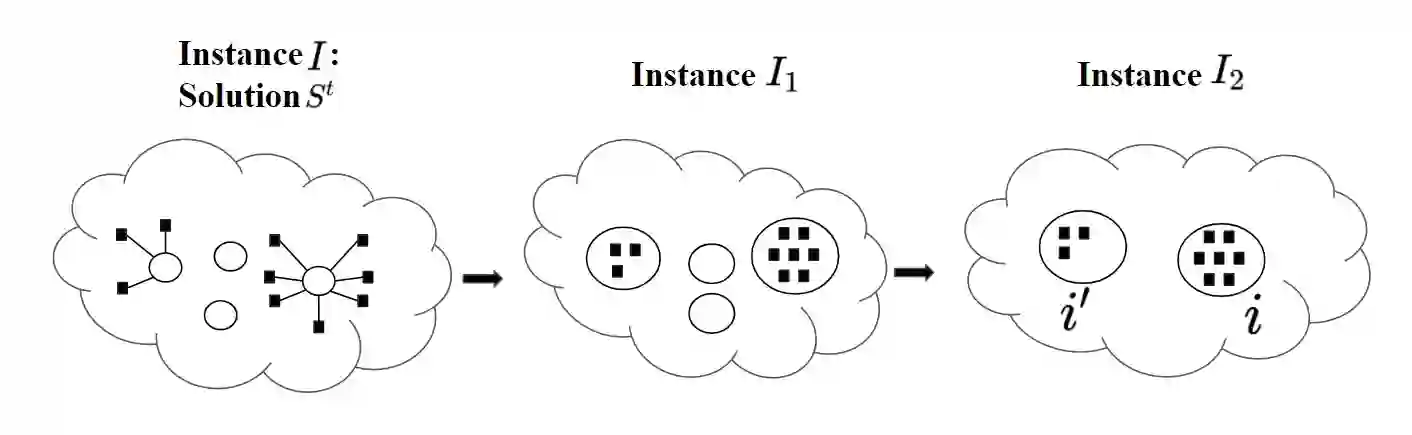
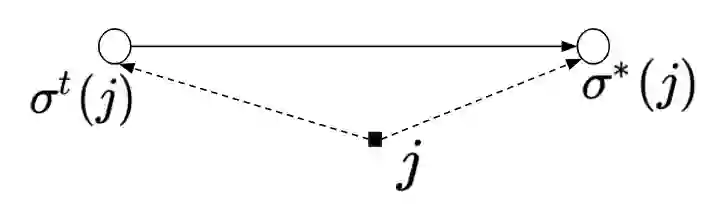
With growing emphasis on e-commerce marketplace platforms where we have a central platform mediating between the seller and the buyer, it becomes important to keep a check on the availability and profitability of the central store. A store serving too less clients can be non-profitable and a store getting too many orders can lead to bad service to the customers which can be detrimental for the business. In this paper, we study the facility location problem(FL) with upper and lower bounds on the number of clients an open facility serves. Constant factor approximations are known for the restricted variants of the problem with only the upper bounds or only the lower bounds. The only work that deals with bounds on both the sides violates both the bounds [8]. In this paper, we present the first (constant factor) approximation for the problem violating the upper bound by a factor of (5/2) without violating the lower bounds when both the lower and the upper bounds are uniform. We first give a tri-criteria (constant factor) approximation violating both the upper and the lower bounds and then get rid of violation in lower bounds by transforming the problem instance to an instance of capacitated facility location problem.
翻译:随着对电子商务市场平台的日益重视,即我们在卖方和买方之间设有一个中央平台的电子商务市场平台,对中央商店的可用性和盈利性进行检查就变得十分重要。服务过少的商店可能无利可图,而收到过多订单的商店可能会给客户带来不良服务,而这种服务对商业有害。在本文中,我们研究了设施位置问题,即开放设施所服务的客户数量有上下限限制;对问题限量变量的常数系数近似度是已知的,只有上限或下限。关于双方界限的唯一工作违反了这两个界限[8]。在本文件中,我们提出了第一个(固定因素)近似的问题,即违反一个因素(5/2),而当下限和上限设施都一致时,不违反下限的下限。我们首先给出一个三标准(固定因素)近似值,即违反上限和下限,然后通过将问题实例转换成一个已设电站的地点问题实例,从而消除下限的违规行为。