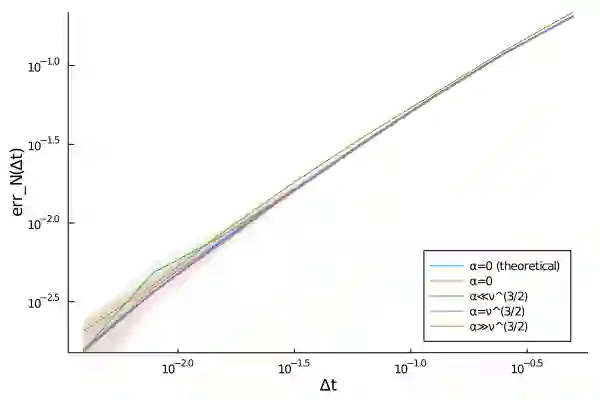
We study the numerical approximation of the invariant measure of a viscous scalar conservation law, one-dimensional and periodic in the space variable, and stochastically forced with a white-in-time but spatially correlated noise. The flux function is assumed to be locally Lipschitz continuous and to have at most polynomial growth. The numerical scheme we employ discretises the SPDE according to a finite-volume method in space, and a split-step backward Euler method in time. As a first result, we prove the well-posedness as well as the existence and uniqueness of an invariant measure for both the semi-discrete and the split-step scheme. Our main result is then the convergence of the invariant measures of the discrete approximations, as the space and time steps go to zero, towards the invariant measure of the SPDE, with respect to the second-order Wasserstein distance. We investigate rates of convergence theoretically, in the case where the flux function is globally Lipschitz continuous with a small Lipschitz constant, and numerically for the Burgers equation.
翻译:我们研究的是,在空间变量中,单维和周期性地,以及用时空白但与空间相关的噪音强行强制的粘合式测量粘度缩进法的数值近似值。通量函数假定是局部的Lipschitz连续的,最多具有多元增长。我们使用的数字方法根据空间的有限体积法和分步后退的Euler方法将SPDE分解。首先,我们证明半分异体和分步制方法的稳妥性以及存在和独特性。我们的主要结果是,随着空间和时间步骤变为零,离散近体的静态测量值与SPDE的静态测量值相趋同,与第二阶级瓦塞施泰因距离有关。我们研究的是理论上的趋同率,如果通量功能是全球范围内的Lipschitz,与一个小的Lipschitz恒定值和布尔格斯方程式的数字一致。