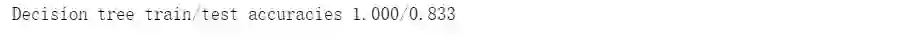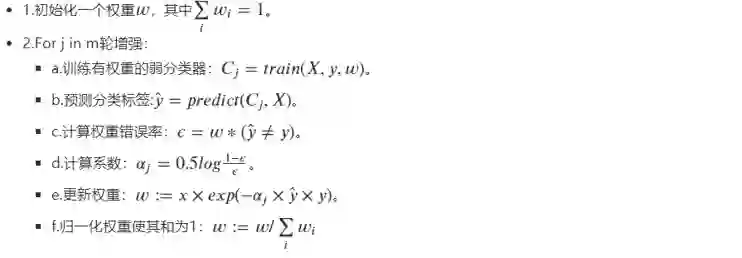机器学习集成学习与模型融合!
来源:Datawhale
对比过kaggle比赛上面的top10的模型,除了深度学习以外的模型基本上都是集成学习的产物。集成学习可谓是上分大杀器,今天就跟大家分享在Kaggle或者阿里天池上面大杀四方的数据科学比赛利器---集成学习。
一、什么是集成学习
-
正所谓“三个臭皮匠赛过诸葛亮”的道理,在机器学习数据挖掘的工程项目中,使用单一决策的弱分类器显然不是一个明智的选择,因为各种分类器在设计的时候都有自己的优势和缺点,也就是说每个分类器都有自己工作偏向,那集成学习就是平衡各个分类器的优缺点,使得我们的分类任务完成的更加优秀。 在大多数情况下,这些基本模型本身的性能并不是非常好,这要么是因为它们具有较高的偏差(例如,低自由度模型),要么是因为他们的方差太大导致鲁棒性不强(例如,高自由度模型)。集成方法的思想是通过将这些弱学习器的偏差和/或方差结合起来,从而创建一个「强学习器」(或「集成模型」),从而获得更好的性能。
集成学习的方法:
-
1. 基于投票思想的多数票机制的集成分类器(MajorityVoteClassifier) -
2. 于bagging思想的套袋集成技术(BaggingClassifier) -
3. 基于boosting思想的自适应增强方法(Adaboost) -
4. 分层模型集成框架stacking(叠加算法)
二、基于投票思想的集成分类器
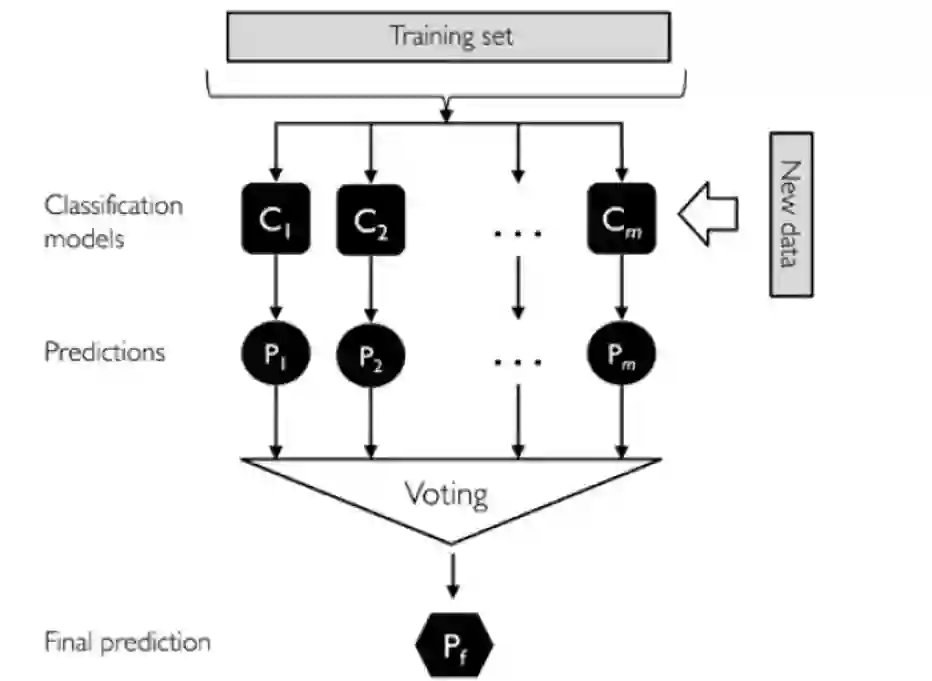
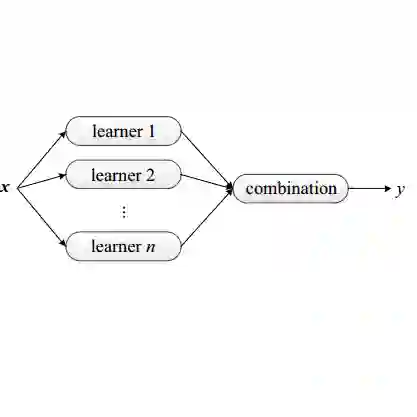
以上是多数投票的流程图:
-
分别训练n个弱分类器。 -
对每个弱分类器输出预测结果,并投票(如下图) 每个样本取投票数最多的那个预测为该样本最终分类预测。
加载相关库:
## 加载相关库
from sklearn.datasets import load_iris # 加载数据
from sklearn.model_selection import train_test_split # 切分训练集与测试集
from sklearn.preprocessing import StandardScaler # 标准化数据
from sklearn.preprocessing import LabelEncoder # 标签化分类变量
初步处理数据
## 初步处理数据
iris = load_iris()
X,y = iris.data[50:,[1,2]],iris.target[50:]
le = LabelEncoder()
y = le.fit_transform(y)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.5,random_state=1,stratify=y)
我们使用训练集训练三种不同的分类器:逻辑回归 + 决策树 + k-近邻分类器
## 我们使用训练集训练三种不同的分类器:逻辑回归 + 决策树 + k-近邻分类器
from sklearn.model_selection import cross_val_score # 10折交叉验证评价模型
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.pipeline import Pipeline # 管道简化工作流
clf1 = LogisticRegression(penalty='l2',C=0.001,random_state=1)
clf2 = DecisionTreeClassifier(max_depth=1,criterion='entropy',random_state=0)
clf3 = KNeighborsClassifier(n_neighbors=1,p=2,metric="minkowski")
pipe1 = Pipeline([['sc',StandardScaler()],['clf',clf1]])
pipe3 = Pipeline([['sc',StandardScaler()],['clf',clf3]])
clf_labels = ['Logistic regression','Decision tree','KNN']
print('10-folds cross validation :\n')
for clf,label in zip([pipe1,clf2,pipe3],clf_labels):
scores = cross_val_score(estimator=clf,X=X_train,y=y_train,cv=10,scoring='roc_auc')
print("ROC AUC: %0.2f(+/- %0.2f)[%s]"%(scores.mean(),scores.std(),label))我们使用MajorityVoteClassifier集成:
## 我们使用MajorityVoteClassifier集成:
from sklearn.ensemble import VotingClassifier
mv_clf = VotingClassifier(estimators=[('pipe1',pipe1),('clf2',clf2),('pipe3',pipe3)],voting='soft')
clf_labels += ['MajorityVoteClassifier']
all_clf = [pipe1,clf2,pipe3,mv_clf]
print('10-folds cross validation :\n')
for clf,label in zip(all_clf,clf_labels):
scores = cross_val_score(estimator=clf,X=X_train,y=y_train,cv=10,scoring='roc_auc')
print("ROC AUC: %0.2f(+/- %0.2f)[%s]"%(scores.mean(),scores.std(),label))
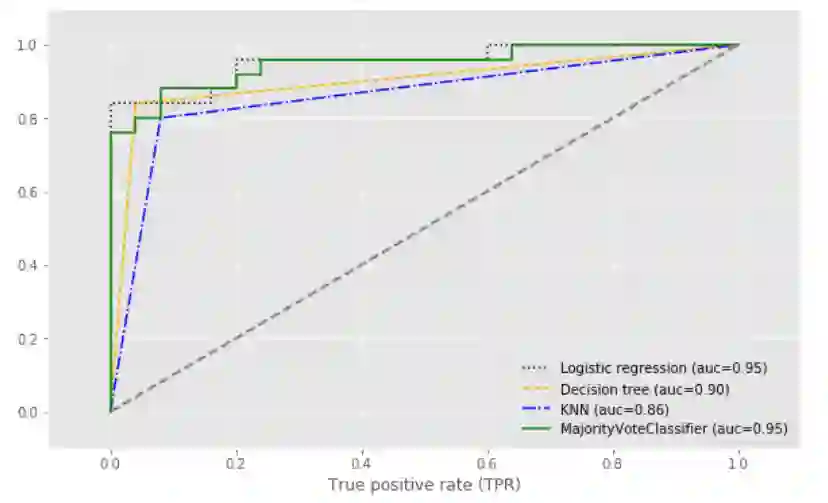
## 对比下面结果,可以得知多数投票方式的分类算法,抗差能力更强。
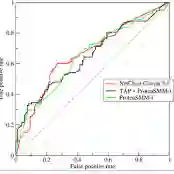
使用ROC曲线评估集成分类器:
## 使用ROC曲线评估集成分类器
from sklearn.metrics import roc_curve
from sklearn.metrics import auc
colors = ['black','orange','blue','green']
linestyles = [':','--','-.','-']
plt.figure(figsize=(10,6))
for clf,label,clr,ls in zip(all_clf,clf_labels,colors,linestyles):
y_pred = clf.fit(X_train,y_train).predict_proba(X_test)[:,1]
fpr,tpr,trhresholds = roc_curve(y_true=y_test,y_score=y_pred)
roc_auc = auc(x=fpr,y=tpr)
plt.plot(fpr,tpr,color=clr,linestyle=ls,label='%s (auc=%0.2f)'%(label,roc_auc))
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],linestyle='--',color='gray',linewidth=2)
plt.xlim([-0.1,1.1])
plt.ylim([-0.1,1.1])
plt.xlabel('False positive rate (FPR)')
plt.xlabel('True positive rate (TPR)')
plt.show()
三、基于bagging思想的套袋集成技术
套袋方法是由柳.布莱曼在1994年的技术报告中首先提出并证明了套袋方法可以提高不稳定模型的准确度的同时降低过拟合的程度(可降低方差)。
套袋方法的流程如下:
注意:套袋方法与投票方法的不同:
投票机制在训练每个分类器的时候都是用相同的全部样本,而Bagging方法则是使用全部样本的一个随机抽样,每个分类器都是使用不同的样本进行训练。其他都是跟投票方法一模一样!
-
对训练集随机采样 -
分别基于不同的样本集合训练n个弱分类器。 -
对每个弱分类器输出预测结果,并投票(如下图) -
每个样本取投票数最多的那个预测为该样本最终分类预测。
我们使用葡萄酒数据集进行建模(数据处理):
## 我们使用葡萄酒数据集进行建模(数据处理)
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)
df_wine.columns = ['Class label', 'Alcohol','Malic acid', 'Ash','Alcalinity of ash','Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols','Proanthocyanins','Color intensity', 'Hue','OD280/OD315 of diluted wines','Proline']
df_wine = df_wine[df_wine['Class label'] != 1] # drop 1 class
y = df_wine['Class label'].values
X = df_wine[['Alcohol','OD280/OD315 of diluted wines']].values
from sklearn.model_selection import train_test_split # 切分训练集与测试集
from sklearn.preprocessing import LabelEncoder # 标签化分类变量
le = LabelEncoder()
y = le.fit_transform(y)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=1,stratify=y)
我们使用单一决策树分类:
## 我们使用单一决策树分类:
tree = DecisionTreeClassifier(criterion='entropy',random_state=1,max_depth=None) #选择决策树为基本分类器
from sklearn.metrics import accuracy_score
tree = tree.fit(X_train,y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train,y_train_pred)
tree_test = accuracy_score(y_test,y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train,tree_test))
我们使用BaggingClassifier分类:
## 我们使用BaggingClassifier分类:
from sklearn.ensemble import BaggingClassifier
tree = DecisionTreeClassifier(criterion='entropy',random_state=1,max_depth=None) #选择决策树为基本分类器
bag = BaggingClassifier(base_estimator=tree,n_estimators=500,max_samples=1.0,max_features=1.0,bootstrap=True,
bootstrap_features=False,n_jobs=1,random_state=1)
from sklearn.metrics import accuracy_score
bag = bag.fit(X_train,y_train)
y_train_pred = bag.predict(X_train)
y_test_pred = bag.predict(X_test)
bag_train = accuracy_score(y_train,y_train_pred)
bag_test = accuracy_score(y_test,y_test_pred)
print('Bagging train/test accuracies %.3f/%.3f' % (bag_train,bag_test))
我们可以对比两个准确率,测试准确率较之决策树得到了显著的提高
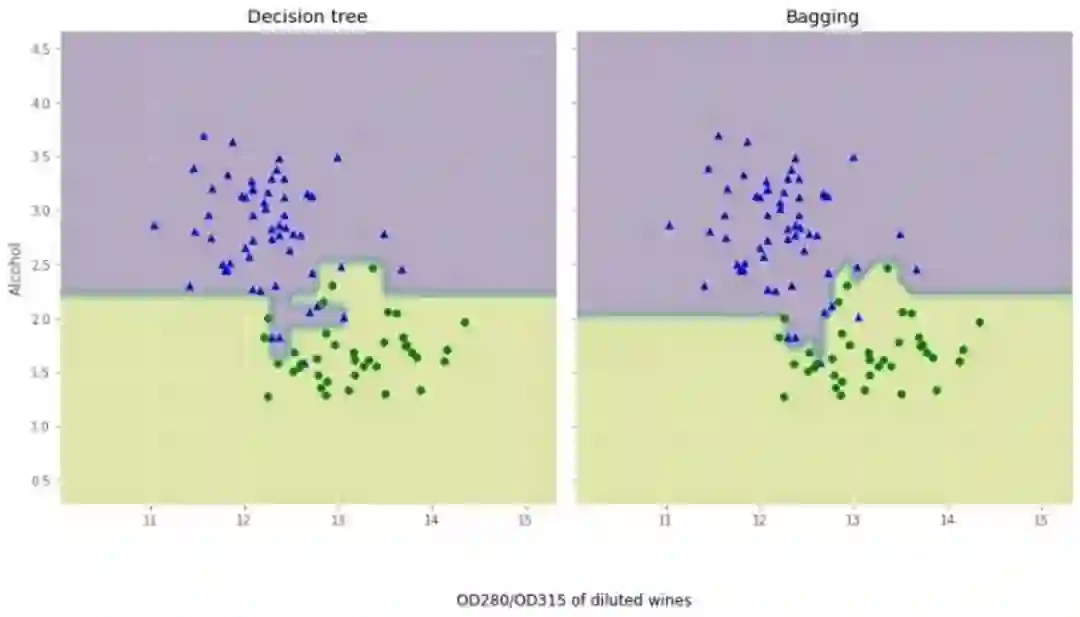
我们来对比下这两个分类方法上的差异:
## 我们来对比下这两个分类方法上的差异
x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))
f, axarr = plt.subplots(nrows=1, ncols=2,sharex='col',sharey='row',figsize=(12, 6))
for idx, clf, tt in zip([0, 1],[tree, bag],['Decision tree', 'Bagging']):
clf.fit(X_train, y_train)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
axarr[idx].contourf(xx, yy, Z, alpha=0.3)
axarr[idx].scatter(X_train[y_train==0, 0],X_train[y_train==0, 1],c='blue', marker='^')
axarr[idx].scatter(X_train[y_train==1, 0],X_train[y_train==1, 1],c='green', marker='o')
axarr[idx].set_title(tt)
axarr[0].set_ylabel('Alcohol', fontsize=12)
plt.tight_layout()
plt.text(0, -0.2,s='OD280/OD315 of diluted wines',ha='center',va='center',fontsize=12,transform=axarr[1].transAxes)
plt.show()
从结果图看起来,三个节点深度的决策树分段线性决策边界在Bagging集成中看起来更加平滑。
四、基于boosting思想的自适应增强方法
Adaboost最初的想法是由Robert E. Schapire在1990年提出的,这个想法叫做自适应增强方法。
与Bagging相比,Boosting思想可以降低偏差。
原始的增强过程具体的实现如下:
AdaBoost的具体步骤如下:
如更新权重如下图:
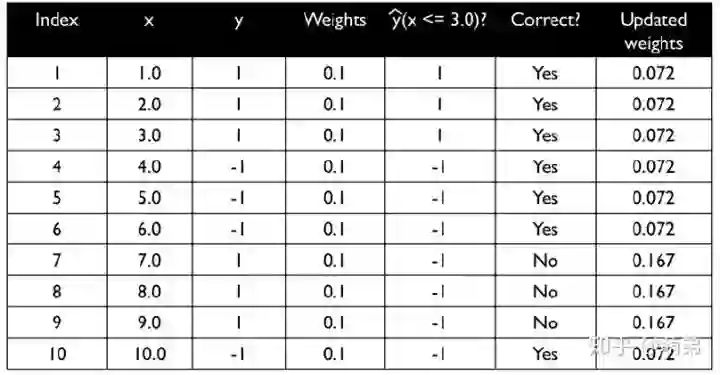
我们用单一决策树建模:
## 我们用单一决策树建模:
from sklearn.ensemble import AdaBoostClassifier
tree = DecisionTreeClassifier(criterion='entropy',random_state=1,max_depth=1)
from sklearn.metrics import accuracy_score
tree = tree.fit(X_train,y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train,y_train_pred)
tree_test = accuracy_score(y_test,y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train,tree_test))
我们使用Adaboost集成建模:
## 我们使用Adaboost集成建模:
ada = AdaBoostClassifier(base_estimator=tree,n_estimators=500,learning_rate=0.1,random_state=1)
ada = ada.fit(X_train,y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train,y_train_pred)
ada_test = accuracy_score(y_test,y_test_pred)
print('Adaboost train/test accuracies %.3f/%.3f' % (ada_train,ada_test))
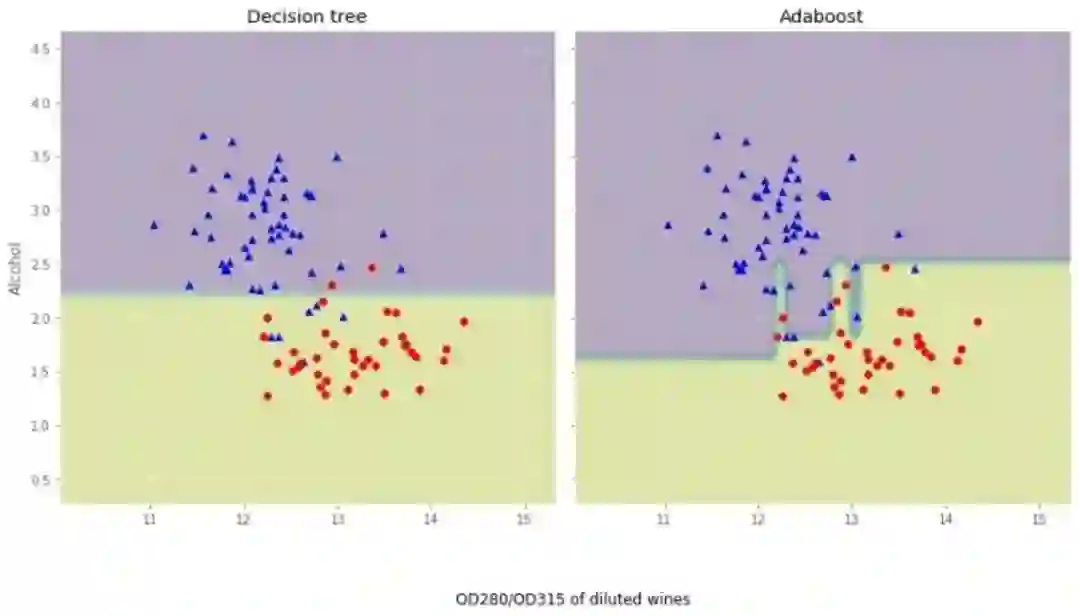
我们观察下Adaboost与决策树的异同:
## 我们观察下Adaboost与决策树的异同
x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))
f, axarr = plt.subplots(nrows=1, ncols=2,sharex='col',sharey='row',figsize=(12, 6))
for idx, clf, tt in zip([0, 1],[tree, ada],['Decision tree', 'Adaboost']):
clf.fit(X_train, y_train)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
axarr[idx].contourf(xx, yy, Z, alpha=0.3)
axarr[idx].scatter(X_train[y_train==0, 0],X_train[y_train==0, 1],c='blue', marker='^')
axarr[idx].scatter(X_train[y_train==1, 0],X_train[y_train==1, 1],c='red', marker='o')
axarr[idx].set_title(tt)
axarr[0].set_ylabel('Alcohol', fontsize=12)
plt.tight_layout()
plt.text(0, -0.2,s='OD280/OD315 of diluted wines',ha='center',va='center',fontsize=12,transform=axarr[1].transAxes)
plt.show()
从结果图看起来,Adaboost决策边界比单层决策树复杂得多!
五、分层模型集成框架stacking(叠加算法)
Stacking集成算法可以理解为一个两层的集成,第一层含有一个分类器,把预测的结果(元特征)提供给第二层, 而第二层的分类器通常是逻辑回归,他把一层分类器的结果当做特征做拟合输出预测结果。
过程如下图:
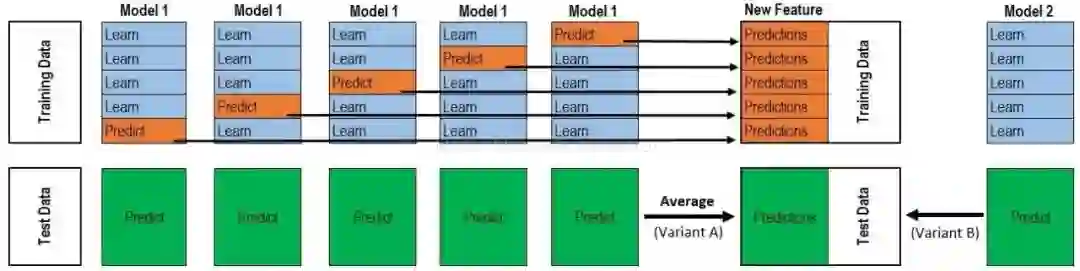
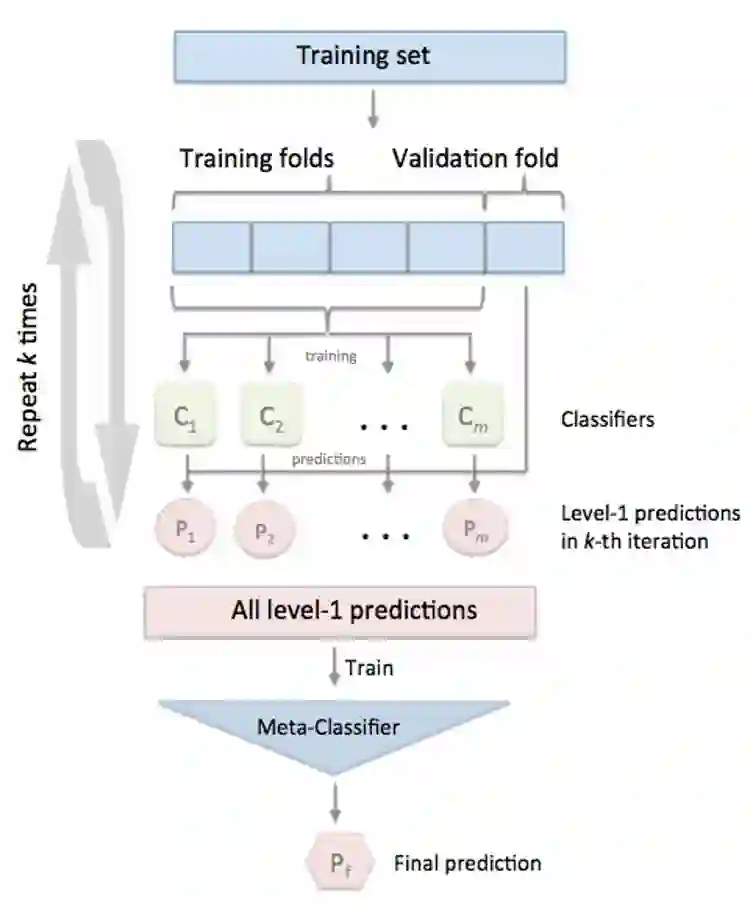
标准的Stacking,也叫Blending如下图:
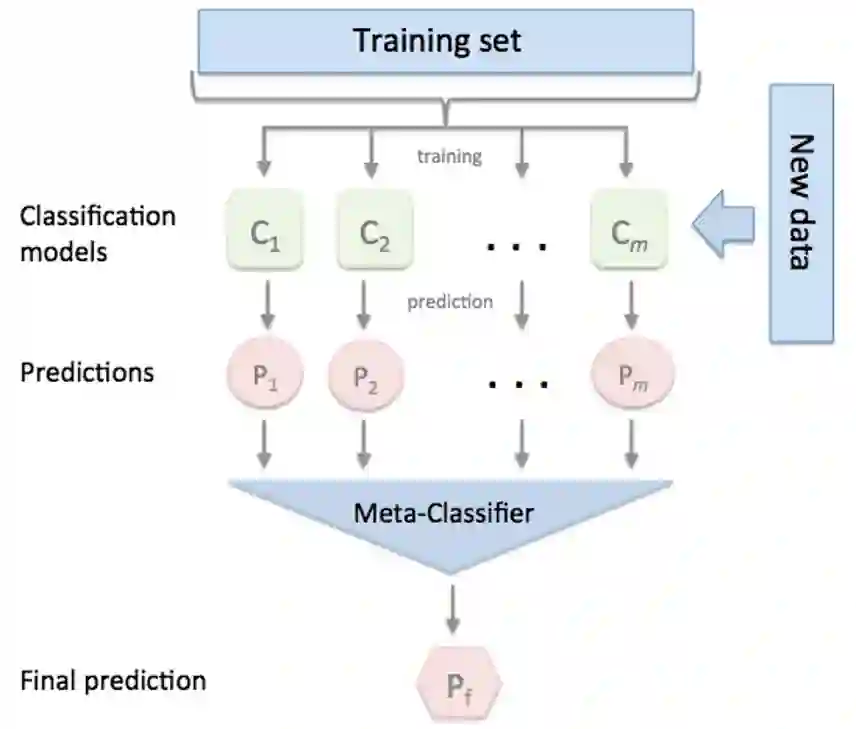
但是,标准的Stacking会导致信息泄露,所以推荐以下Satcking算法:
由于目前sklearn没有Stacking相关的类,因此我们使用mlxtend库!!!!
详细代码内容查看:
http://rasbt.github.io/mlxtend/user_guide/classifier/StackingClassifier/
http://rasbt.github.io/mlxtend/user_guide/classifier/StackingCVClassifier/
1. 简单堆叠3折CV分类:
## 1. 简单堆叠3折CV分类
from sklearn import datasets
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
RANDOM_SEED = 42
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()
# Starting from v0.16.0, StackingCVRegressor supports
# `random_state` to get deterministic result.
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3], # 第一层分类器
meta_classifier=lr, # 第二层分类器
random_state=RANDOM_SEED)
print('3-fold cross validation:\n')
for clf, label in zip([clf1, clf2, clf3, sclf], ['KNN', 'Random Forest', 'Naive Bayes','StackingClassifier']):
scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy')
print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
我们画出决策边界:
## 我们画出决策边界
from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
import itertools
gs = gridspec.GridSpec(2, 2)
fig = plt.figure(figsize=(10,8))
for clf, lab, grd in zip([clf1, clf2, clf3, sclf],
['KNN',
'Random Forest',
'Naive Bayes',
'StackingCVClassifier'],
itertools.product([0, 1], repeat=2)):
clf.fit(X, y)
ax = plt.subplot(gs[grd[0], grd[1]])
fig = plot_decision_regions(X=X, y=y, clf=clf)
plt.title(lab)
plt.show()
2.使用概率作为元特征:
## 2.使用概率作为元特征
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
use_probas=True,
meta_classifier=lr,
random_state=42)
print('3-fold cross validation:\n')
for clf, label in zip([clf1, clf2, clf3, sclf],
['KNN',
'Random Forest',
'Naive Bayes',
'StackingClassifier']):
scores = cross_val_score(clf, X, y,
cv=3, scoring='accuracy')
print("Accuracy: %0.2f (+/- %0.2f) [%s]"
% (scores.mean(), scores.std(), label))
3. 堆叠5折CV分类与网格搜索(结合网格搜索调参优化):
## 3. 堆叠5折CV分类与网格搜索(结合网格搜索调参优化)
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from mlxtend.classifier import StackingCVClassifier
# Initializing models
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
meta_classifier=lr,
random_state=42)
params = {'kneighborsclassifier__n_neighbors': [1, 5],
'randomforestclassifier__n_estimators': [10, 50],
'meta_classifier__C': [0.1, 10.0]}
grid = GridSearchCV(estimator=sclf,
param_grid=params,
cv=5,
refit=True)
grid.fit(X, y)
cv_keys = ('mean_test_score', 'std_test_score', 'params')
for r, _ in enumerate(grid.cv_results_['mean_test_score']):
print("%0.3f +/- %0.2f %r"
% (grid.cv_results_[cv_keys[0]][r],
grid.cv_results_[cv_keys[1]][r] / 2.0,
grid.cv_results_[cv_keys[2]][r]))
print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)
如果我们打算多次使用回归算法,我们要做的就是在参数网格中添加一个附加的数字后缀,如下所示:
## 如果我们打算多次使用回归算法,我们要做的就是在参数网格中添加一个附加的数字后缀,如下所示:
from sklearn.model_selection import GridSearchCV
# Initializing models
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf1, clf2, clf3],
meta_classifier=lr,
random_state=RANDOM_SEED)
params = {'kneighborsclassifier-1__n_neighbors': [1, 5],
'kneighborsclassifier-2__n_neighbors': [1, 5],
'randomforestclassifier__n_estimators': [10, 50],
'meta_classifier__C': [0.1, 10.0]}
grid = GridSearchCV(estimator=sclf,
param_grid=params,
cv=5,
refit=True)
grid.fit(X, y)
cv_keys = ('mean_test_score', 'std_test_score', 'params')
for r, _ in enumerate(grid.cv_results_['mean_test_score']):
print("%0.3f +/- %0.2f %r"
% (grid.cv_results_[cv_keys[0]][r],
grid.cv_results_[cv_keys[1]][r] / 2.0,
grid.cv_results_[cv_keys[2]][r]))
print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)
4.在不同特征子集上运行的分类器的堆叠:
## 4.在不同特征子集上运行的分类器的堆叠
###不同的1级分类器可以适合训练数据集中的不同特征子集。以下示例说明了如何使用scikit-learn管道和ColumnSelector:
from sklearn.datasets import load_iris
from mlxtend.classifier import StackingCVClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
iris = load_iris()
X = iris.data
y = iris.target
pipe1 = make_pipeline(ColumnSelector(cols=(0, 2)), # 选择第0,2列
LogisticRegression())
pipe2 = make_pipeline(ColumnSelector(cols=(1, 2, 3)), # 选择第1,2,3列
LogisticRegression())
sclf = StackingCVClassifier(classifiers=[pipe1, pipe2],
meta_classifier=LogisticRegression(),
random_state=42)
sclf.fit(X, y)
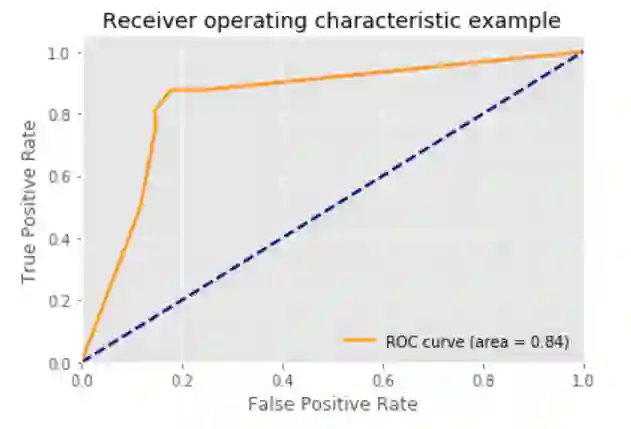
5.ROC曲线 decision_function:
## 5.ROC曲线 decision_function
### 像其他scikit-learn分类器一样,它StackingCVClassifier具有decision_function可用于绘制ROC曲线的方法。
### 请注意,decision_function期望并要求元分类器实现decision_function。
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
iris = datasets.load_iris()
X, y = iris.data[:, [0, 1]], iris.target
# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]
RANDOM_SEED = 42
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.33, random_state=RANDOM_SEED)
clf1 = LogisticRegression()
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = SVC(random_state=RANDOM_SEED)
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
meta_classifier=lr)
# Learn to predict each class against the other
classifier = OneVsRestClassifier(sclf)
y_score = classifier.fit(X_train, y_train).decision_function(X_test)
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
plt.figure()
lw = 2
plt.plot(fpr[2], tpr[2], color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()