漫画：什么是红黑树？

作者 | 小灰

来源 | 程序员小灰（ID：chengxuyuanxiaohui）

2017年，小灰曾经发布过一篇关于红黑树的漫画，当时由于时间仓促，部分知识点一带而过，并没有讲解得很细致全面。

最近，小灰把这个知识点重新做了总结，分成上下两篇，希望大家把红黑树这个重要的数据结构彻底吃透。

—————  第二天  —————

————————————

二叉查找树（BST）具备什么特性呢？

1.左子树上所有结点的值均小于或等于它的根结点的值。

2.右子树上所有结点的值均大于或等于它的根结点的值。

3.左、右子树也分别为二叉排序树。

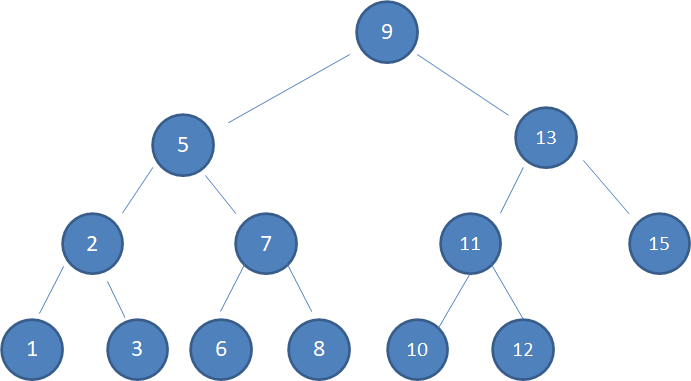
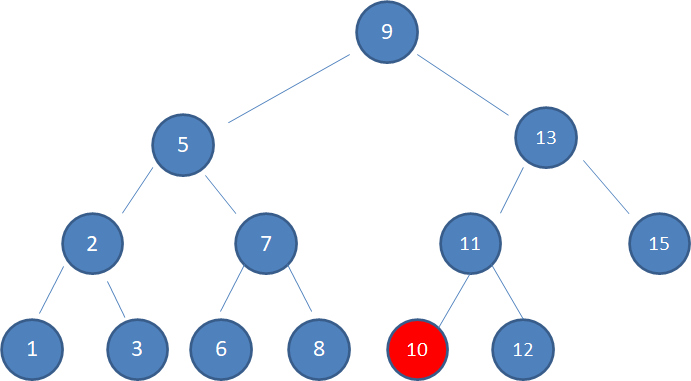
下图中这棵树，就是一颗典型的二叉查找树：

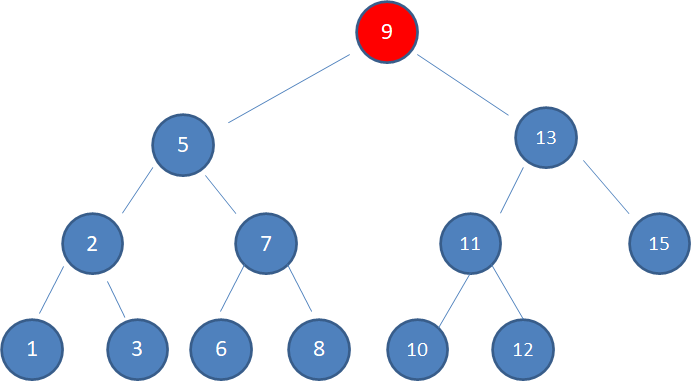
1.查看根结点9：

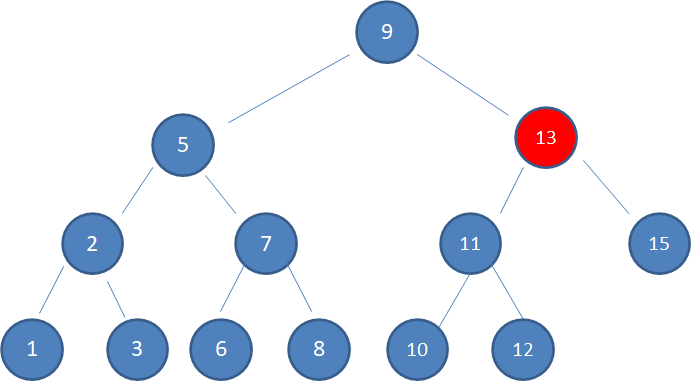
2.根据二叉查找树左子树小、右子树大的特性，10 > 9，因此值为10的结点只可能在根结点的右子树当中，我们查看右孩子结点13：

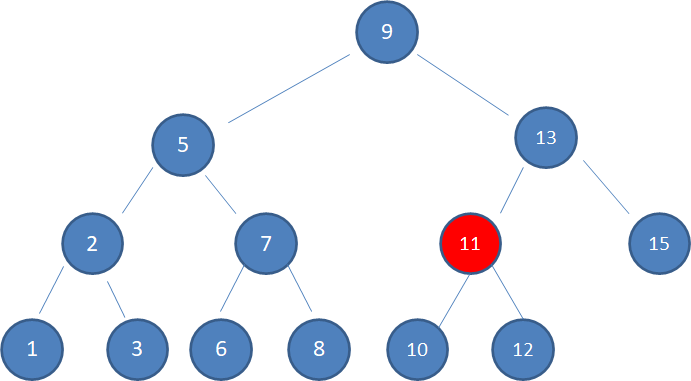
3.由于10 < 13，因此查看左孩子11：

4.由于10 < 11，因此查看左孩子10，发现10正是要查找的结点：

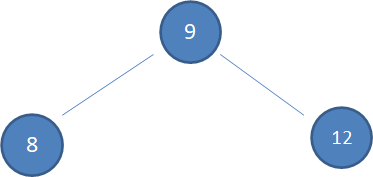
假设初始的二叉查找树只有三个结点，根结点值为9，左孩子值为8，右孩子值为12：

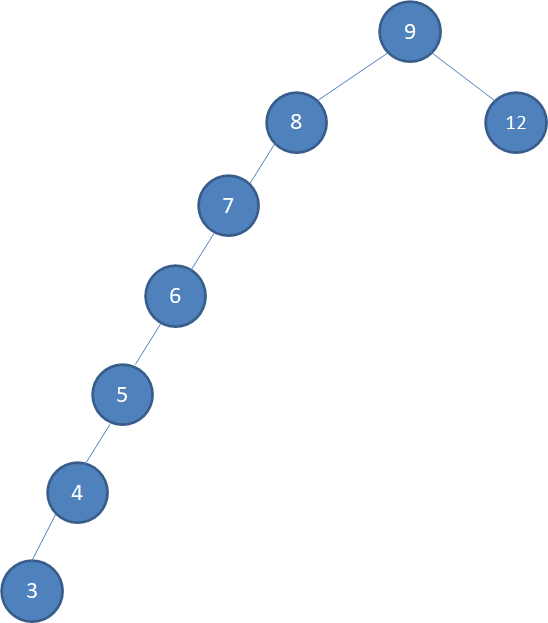
接下来我们依次插入如下五个结点：7,6,5,4,3。依照二叉查找树的特性，结果会变成什么样呢？

1.结点是红色或黑色。

2.根结点是黑色。

3.每个叶子结点都是黑色的空结点（NIL结点）。

4 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)

5.从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。

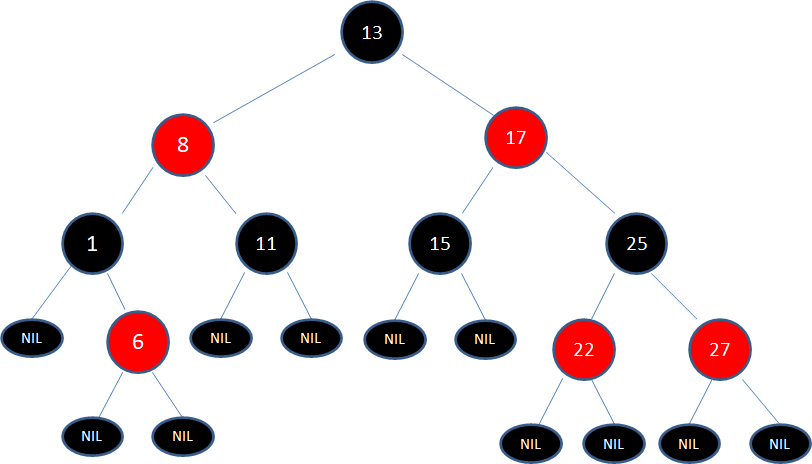
下图中这棵树，就是一颗典型的红黑树：

什么情况下会破坏红黑树的规则，什么情况下不会破坏规则呢？我们举两个简单的例子：

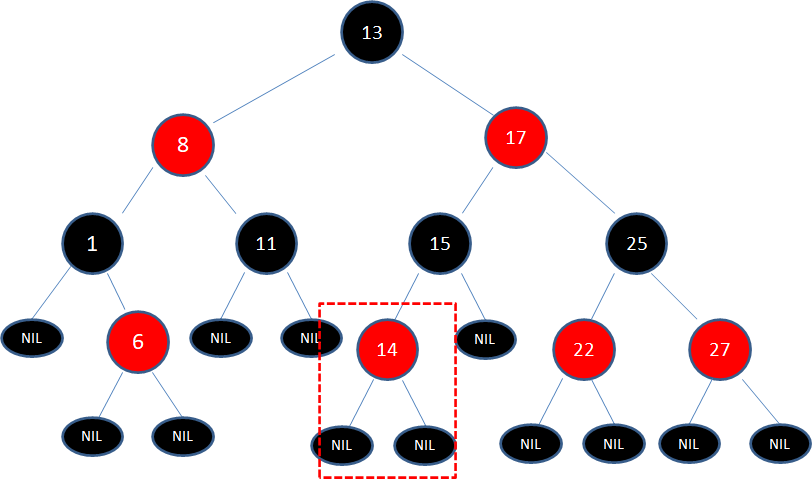
1.向原红黑树插入值为14的新结点：

由于父结点15是黑色结点，因此这种情况并不会破坏红黑树的规则，无需做任何调整。

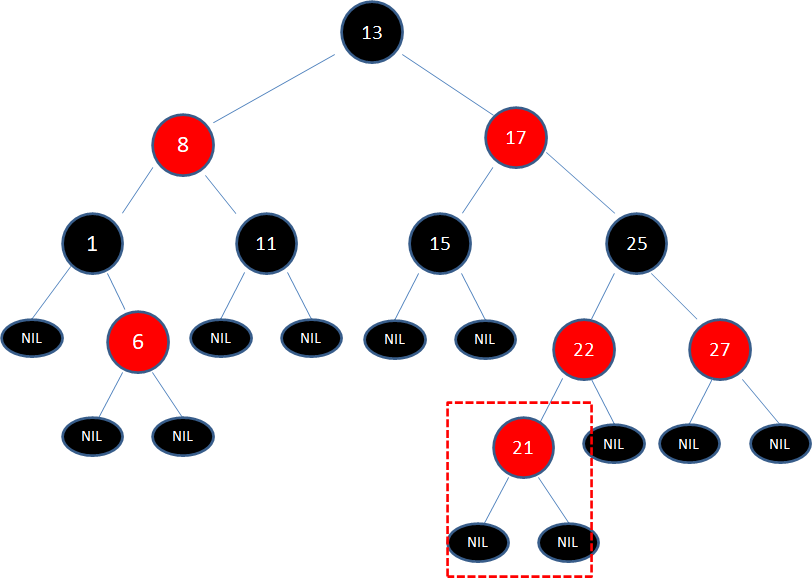
2.向原红黑树插入值为21的新结点：

由于父结点22是红色结点，因此这种情况打破了红黑树的规则4（每个红色结点的两个子结点都是黑色），必须进行调整，使之重新符合红黑树的规则。

变色：

为了重新符合红黑树的规则，尝试把红色结点变为黑色，或者把黑色结点变为红色。

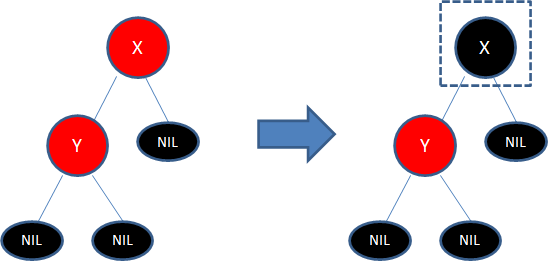
下图所表示的是红黑树的一部分（子树），新插入的结点Y是红色结点，它的父亲结点X也是红色的，不符合规则4，因此我们可以把结点X从红色变成黑色：

但是，仅仅把一个结点变色，会导致相关路径凭空多出一个黑色结点，这样就打破了规则5。因此，我们需要对其他结点做进一步的调整，后文会详细说明。

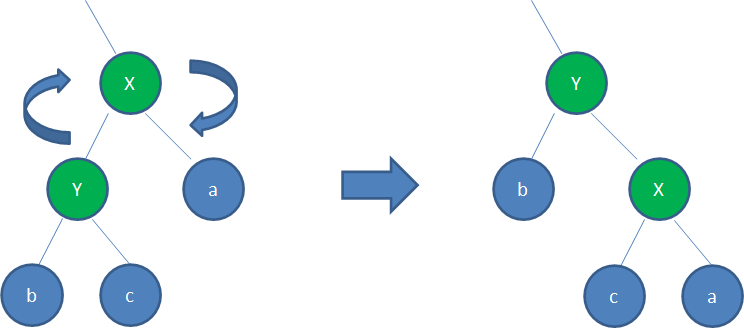
左旋转：

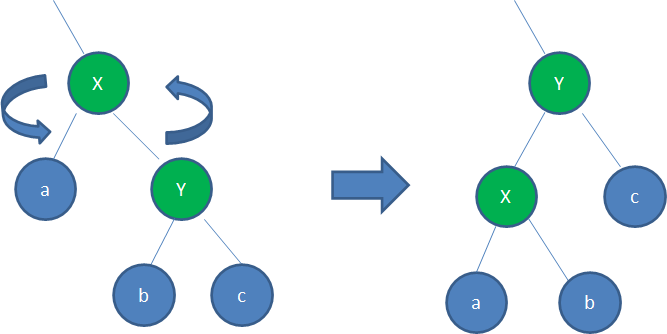
逆时针旋转红黑树的两个结点，使得父结点被自己的右孩子取代，而自己成为自己的左孩子。说起来很怪异，大家看下图：

图中，身为右孩子的Y取代了X的位置，而X变成了自己的左孩子。此为左旋转。

右旋转：

顺时针旋转红黑树的两个结点，使得父结点被自己的左孩子取代，而自己成为自己的右孩子。大家看下图：

图中，身为左孩子的Y取代了X的位置，而X变成了自己的右孩子。此为右旋转。

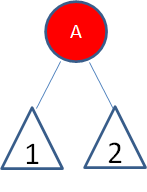
局面1：新结点（A）位于树根，没有父结点。

(空心三角形代表结点下面的子树)

这种局面，直接让新结点变色为黑色，规则2得到满足。同时，黑色的根结点使得每条路径上的黑色结点数目都增加了1，所以并没有打破规则5。

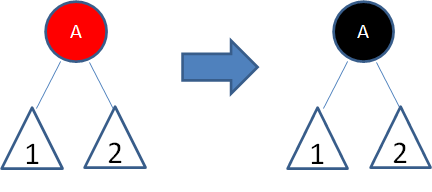
局面2：新结点（B）的父结点是黑色。

这种局面，新插入的红色结点B并没有打破红黑树的规则，所以不需要做任何调整。

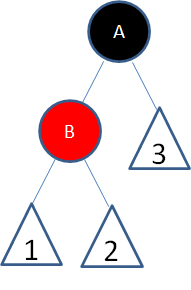
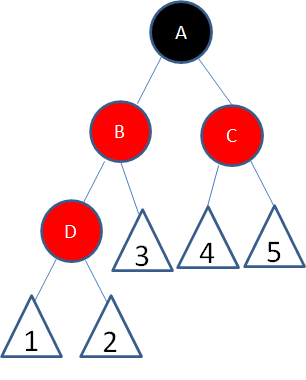
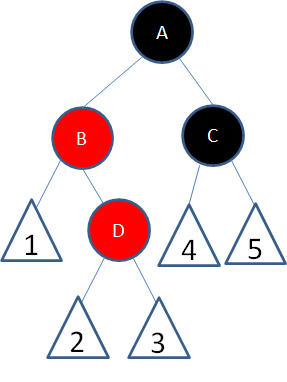
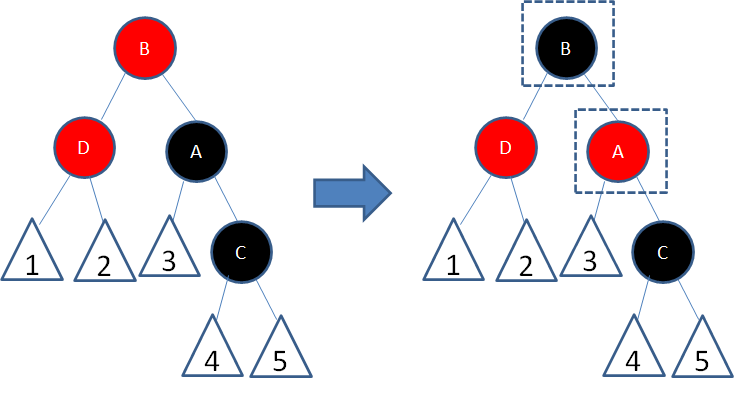
局面3：新结点（D）的父结点和叔叔结点都是红色。

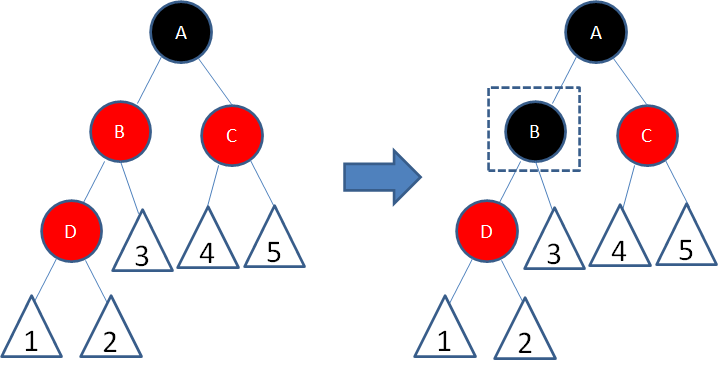
这种局面，两个红色结点B和D连续，违反了规则4。因此我们先让结点B变为黑色：

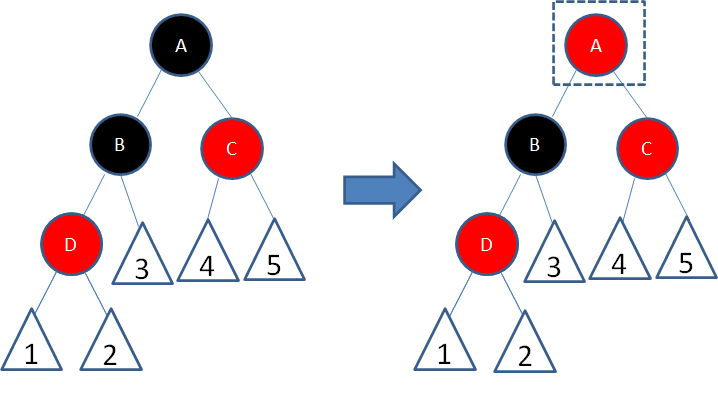
这样一来，结点B所在路径凭空多了一个黑色结点，打破了规则5。因此我们让结点A变为红色：

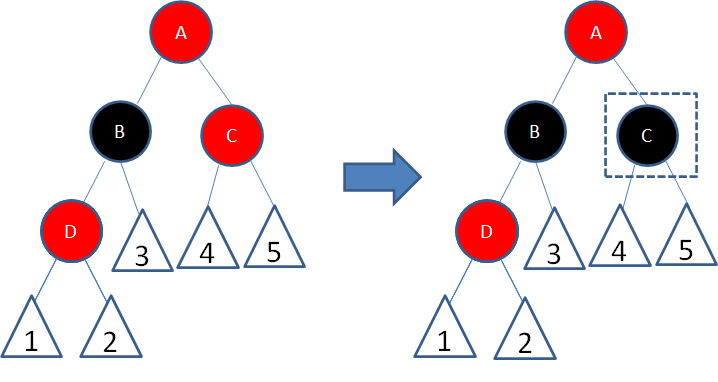
这时候，结点A和C又成为了连续的红色结点，我们再让结点C变为黑色：

经过上面的调整，这一局部重新符合了红黑树的规则。

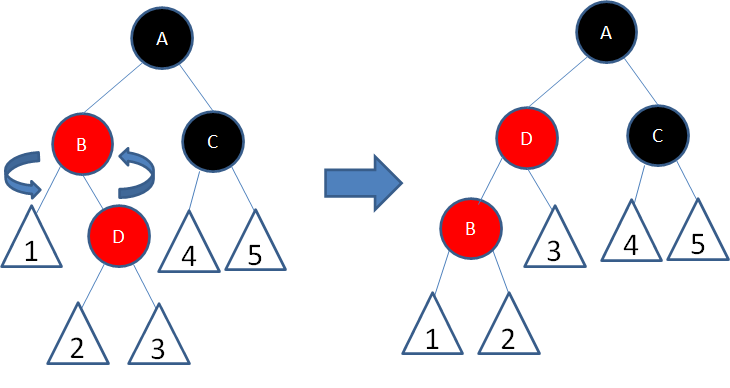
局面4：新结点（D）的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的右孩子，父结点（B）是祖父结点的左孩子。

我们以结点B为轴，做一次左旋转，使得新结点D成为父结点，原来的父结点B成为D的左孩子：

这样一来，进入了局面5。

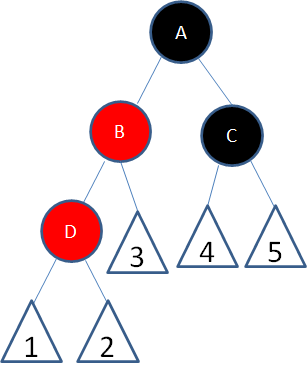
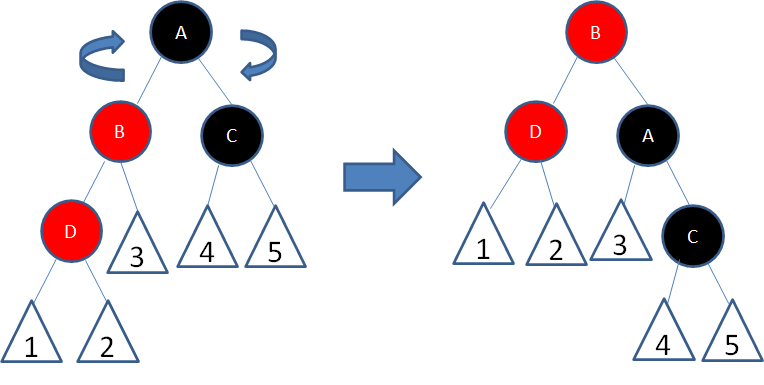
局面5：新结点（D）的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的左孩子，父结点（B）是祖父结点的左孩子。

我们以结点A为轴，做一次右旋转，使得结点B成为祖父结点，结点A成为结点B的右孩子：

接下来，我们让结点B变为黑色，结点A变为红色：

经过上面的调整，这一局部重新符合了红黑树的规则。

以上就是红黑树插入操作所涉及的5种局面。

或许有人会问，如果局面4和局面5当中的父结点B是祖父结点A的右孩子该怎么办呢？

很简单，如果局面4中的父结点B是右孩子，则成为了局面5的镜像，原本的右旋操作改为左旋；如果局面5中的父结点B是右孩子，则成为了局面4的镜像，原本的左旋操作改为右旋。

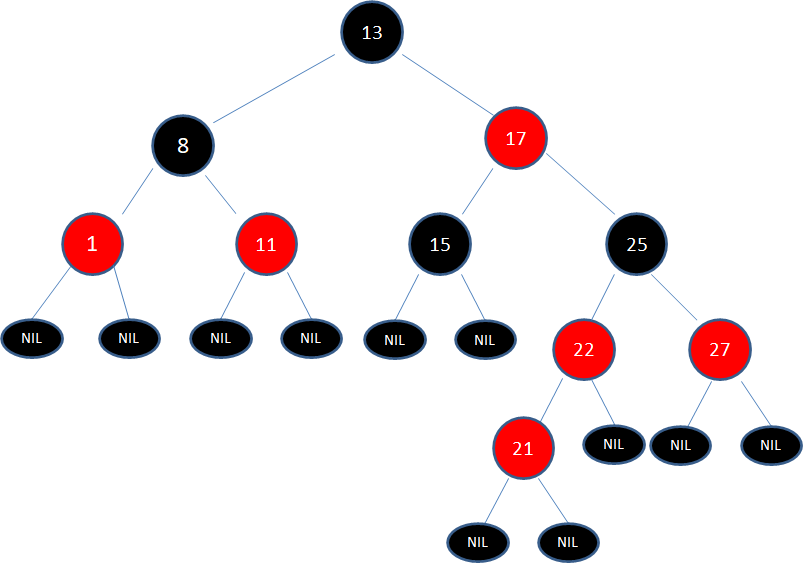
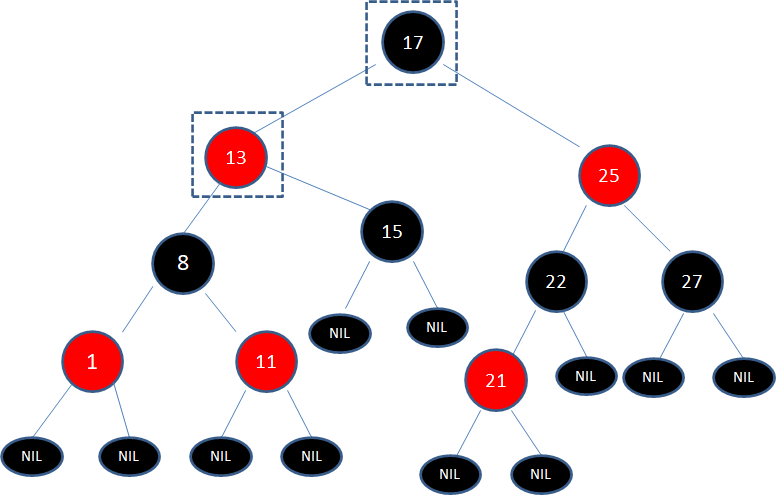
给定下面这颗红黑树，新插入的结点是21：

显然，新结点21和它的父结点22是连续的红色结点，违背了规则4，我们应该如何调整呢？

让我们回顾一下刚才讲的5种局面，当前的情况符合局面3：

“新结点的父结点和叔叔结点都是红色。”

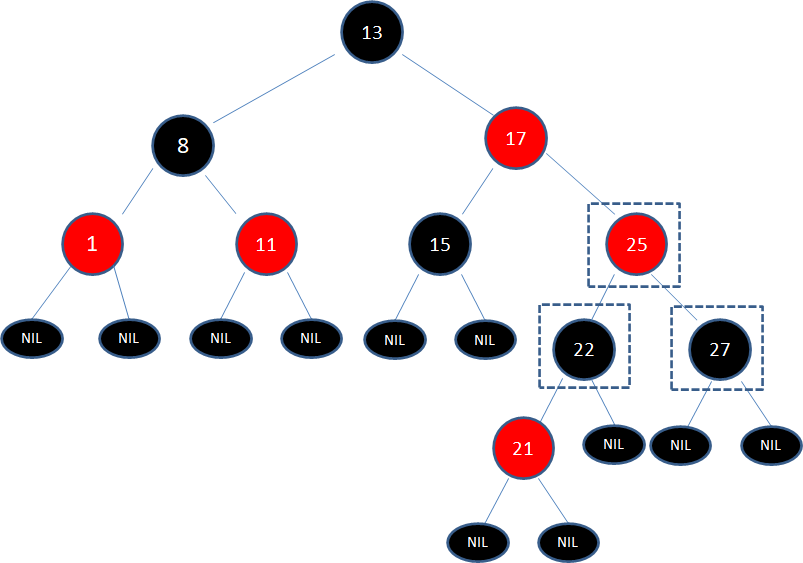
于是我们经过三次变色，22变为黑色，25变为红色，27变为黑色：

经过上面的调整，以结点25为根的子树符合了红黑树规则，但结点25和结点17成为了连续的红色结点，违背规则4。

于是，我们把结点25看做一个新结点，正好符合局面5的镜像：

“新结点的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的右孩子，父结点是祖父结点的右孩子”

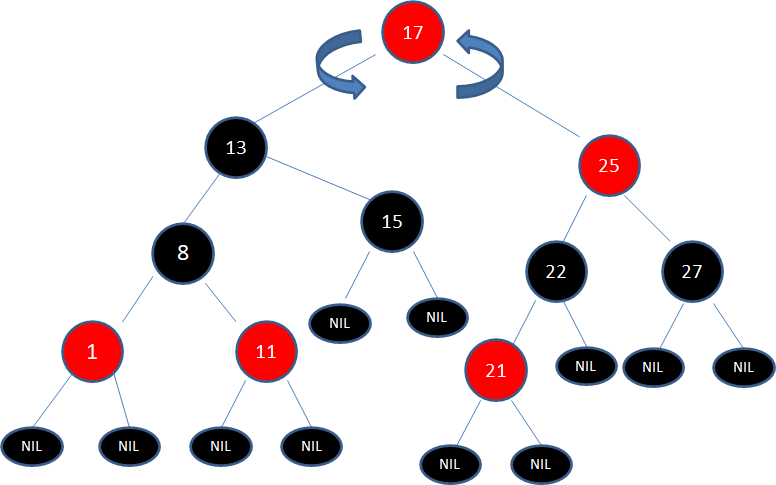
于是我们以根结点13为轴进行左旋转，使得结点17成为了新的根结点：

接下来，让结点17变为黑色，结点13变为红色：

如此一来，我们的红黑树变得重新符合规则。

想看更多小灰用漫画讲算法？可以戳下方小程序查看：

更多精彩推荐
☞再见 Python，Hello Julia！
☞顺丰正式杀入外卖领域；中国移动推出 5G 消息 App；GCC 10.1 发布 | 极客头条
☞你现在从事的程序员还有多久会消失？牛津大学研究员帮你算了算
☞一次对语音技术的彻底批判
☞后端程序员必备：书写高质量SQL的30条建议
☞到底是哪些人在玩链游？| 《区块链游戏玩家研究报告》
你点的每个“在看”，我都认真当成了喜欢