如何在雨天百分之百防淋湿

会员服务 ·

如何在雨天百分之百防淋湿

2018 年 4 月 13 日 果壳网 赖以威

一个人的姿态很重要。

然而，生活中有许多处境，让我们无法一直好好保持挺直的姿态，特别是在梧桐花开的五月，或是整天蝉鸣的七八月，那些梅雨、台风的季节。

在雨中撑伞，还想做到“立如松，行如风”，除了靠意志力，恐怕需要数学的辅佐。

为什么我打着伞还是淋湿了

想象一下这样的情节：一位大和尚和几个徒弟四处化缘，他们走在一望无际的草原上。天空中厚重的乌云，忽然像被人拧过了一般，下起了雨。众人撑起雨伞，继续前进。

大和尚注意到高徒弟将伞撑得很低，甚至弓起了背，整个人弯腰蜷缩在伞底下。他摇了摇头，怎么这些徒弟不懂得观察师傅呢。

“徒儿们，看看为师，不弯腰驼背，身上一点也没湿。”

仔细一瞧，大和尚身子挺得笔直，伞也举得老高，但下摆干干的，一滴雨水也没有。

“因为师父比较矮？”

大和尚愣了一下，脸上闪过一片红色，他回答：

“虽然这是事实，也是原因之一，不过不是关键。重点是，面对雨水的迎击，不需要让自己变矮，变小。只要懂得‘后退’就好。”

“师父在说禅吗？”

“不，我在说数学。”

大和尚用手杖在地上画了一幅图：

制图：赖以威

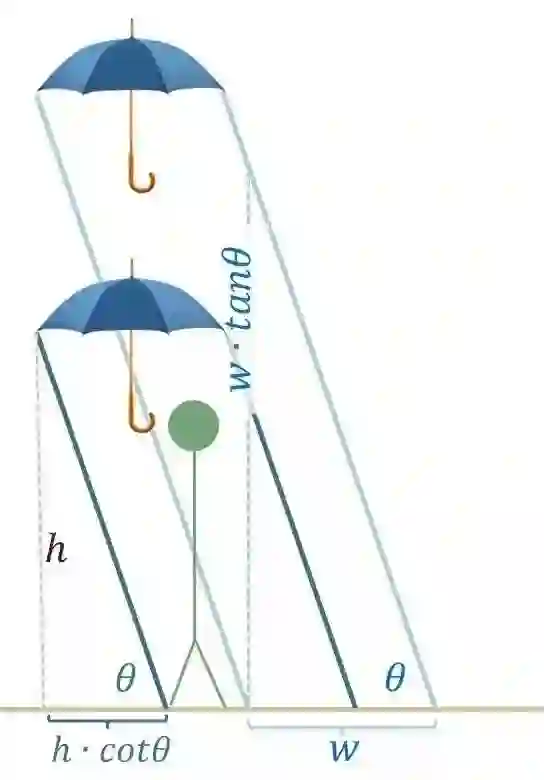
“这是我们在雨中行走的截面图。假设雨跟地面夹角为θ，拿伞的高度为h，伞的宽w。

你们看，当雨是斜的，伞的遮蔽范围将从长方形变成平行四边形，伞正下方h·cotθ的范围都会被雨淋湿。伞拿低一点让h变小，的确有帮助。但更正确的方式，应该是往后退h·cotθ，即可确保裤管不会被淋湿。”

大和尚顿了顿，继续说：

“不是常跟你们提起，要时时注意四威仪，‘立如松、行如风’吗。只要懂得这个道理，雨天不用驼背走路，还可以将伞举得更高，更英挺，只要算好后退距离，依然得保全身不湿。”

徒弟们照着师父的话做了后，虽然伞举再头前，看起来有点像和尚版的自由女神像，但绑腿的确不再被雨淋湿了。正当大伙儿赞叹师父博学多闻时，高徒弟发问：

“师父，徒儿脚没湿，可是脸却湿了。”

众人一看，只见他脸上满是雨水，甚至僧袍领口颜色都变深了，那模样有些滑稽。大和尚笑了笑，低声说：

“谁叫你长那么高，活该。”

“师父说什么？”

“噢，没有。为师说，因为你长太高了，要是雨打得斜，注定会被淋到的。

从方才图的例子可以看到，要是伞拿低一点，遮雨的高度跟伞高度一样是h，但当伞拿高一点时，遮雨的高度即是w·tanθ，竟然跟伞的宽度w和雨的斜度有关。而遮雨的高度是(h，w·tanθ)两个数值取较小值。换句话说，只要身高高于w·tanθ的人，终究难逃被淋湿的命运。往后退，就像你现在这样，脚不湿，但上半身却淋湿了。”

大和尚边说，边用手杖又画了个图：

绘图：赖以威

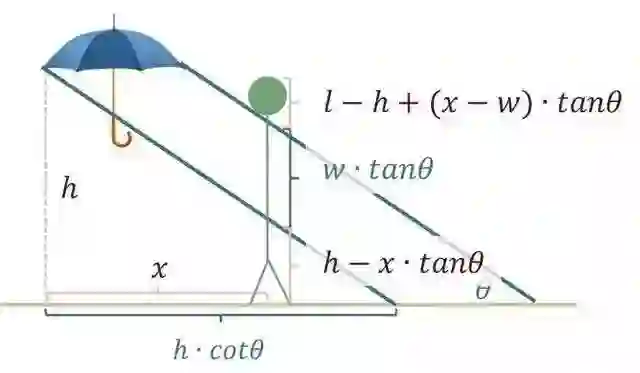
“这时，只好做出取舍，要让裤管淋湿多少？头淋湿多少？这样的取舍可以靠调整伞的高度，和后退的幅度来达成。

除了雨斜度θ、伞举的高度h、宽度w，再假设三个数字，后退幅度x，身高l，以及裤管会湿掉的高度z。z可以利用相似三角形的概念求得：

h·cotθ:z=h:(h·cotθ-x)；

z=h-x·tanθ；

也就是说，裤管直到h-x·tanθ的高度都会湿掉。中间身体w·tanθ的部分不会湿。上半身从天灵盖往下l-h+(x-w) ·tanθ的部位都会湿掉。”

大和尚将自己背上遮阳的斗笠卸下，递给高徒弟，“你算好后，再调整斗笠戴的位置跟角度，用斗笠遮住上半身的雨势吧。驼背让l变小，的确可以降低淋到雨的部位，但有违修行，还是别做了。”

何不让伞面与雨线垂直相交

走了一个时辰，雨势不但没趋缓，上天彷佛在考验众人，还加强风势，让雨变得更斜，这下，除了最高的徒弟外，其他人也纷纷戴上斗笠，除了大和尚依然不用。

意外发现“原来我最矮啊”的大和尚，看着这些徒儿为了恪守他的教训，在雨中不驼背，虽然还是有些气他们怎么都那么高，活该被雨淋，但想了想，还是决定再传授他们一道心法。

“把伞拿斜吧。”

“拿多斜呢，师父。”

“跟雨势垂直。”

大和尚又拿起手杖，在地上画着：

绘图：赖以威

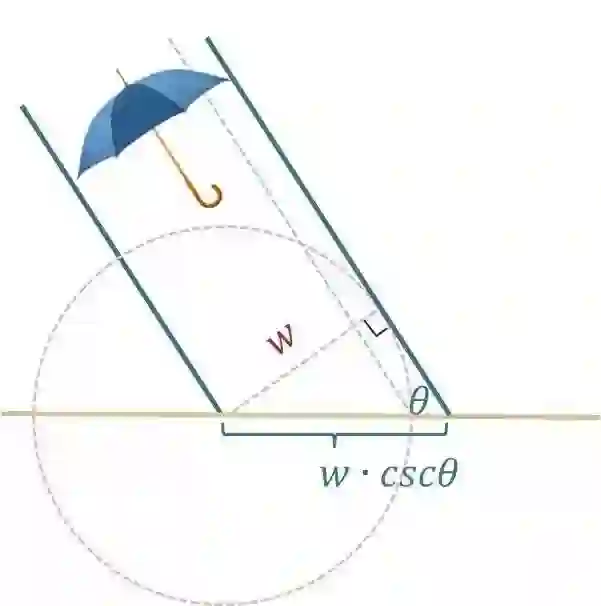
“我们可以用这图来证明‘伞与雨势垂直’为最佳拿法。

将伞一端投影到地表上的点为圆心，伞宽为半径，可以画出图中的圆。再给定下雨方向为斜率，过圆上一点，符合‘点斜式’所需条件，即能画出一条直线。直线跟地表相接的点，与圆心之间的距离是避雨区域，水平拿伞时，此区域长度是w乘上tanθ，即得到可遮雨高度w·tanθ。现在，当伞拿的角度与雨势垂直，这条线就会变成圆的切线，通过圆上一点，线跟圆心的距离最远，避雨区域最大，变成w·secθ。”

大和尚抬头看，每一位徒弟，脸上没被雨淋到，却湿淋淋地“一头雾水”。他只好换个方式解释：

“你们试试看，从原本水平拿伞，慢慢变斜，会淋到雨的部分越来越少，在某个角度会达到最大值，之后再更斜时，反而又会变小。对吧？”

徒弟们转动手腕尝试，点头响应师父。

“再看刚刚地上这张图，要是伞跟雨势不垂直，这条线会变成割线，和圆相交两点，要是这个角度是最大值，就表示有另一个角度也会提供最大的遮雨高度，两个最大值，违反你们实际操作的体验。”

徒弟们纷纷发出“噢噢”的声音，像是知识被扔进了他们的心中，发出的回响。大和尚最喜欢听到这种反应了。

这时，最机灵的小徒弟开口了：

“师父，所以说，要是搭配第一张图，遮雨高度即会从原本的w·tanθ变成w·secθ，各自可以再写成w·sinθ/cosθ和w /cosθ，前者比后者多了sinθ倍，因为sinθ永远小于1，所以当伞拿斜，永远会比伞拿直的能遮住更多。”

“很好，你说的没错。”

大和尚满意地点点头。

“虽然数学是世间法，但有些时候，世间法也能帮助我们修行的。”

看着地上的图，大和尚忽然转身问最高的徒弟身高。

答曰“一米八四。”