NeurIPS 2021 奖项公布,6 篇论文获得杰出论文奖,1 篇获得时间检验奖,此外,今年新增数据集和基准 Track 最佳论文奖,分别由加州大学洛杉矶分校、斯坦福大学的研究者摘得。
NeurIPS 2021 将于下周正式开幕,今年组委会提前公布了杰出论文奖、时间检验奖,以及一项新的奖项——数据集和基准 Track 最佳论文奖(Datasets and Benchmarks Track Best Paper Awards)。
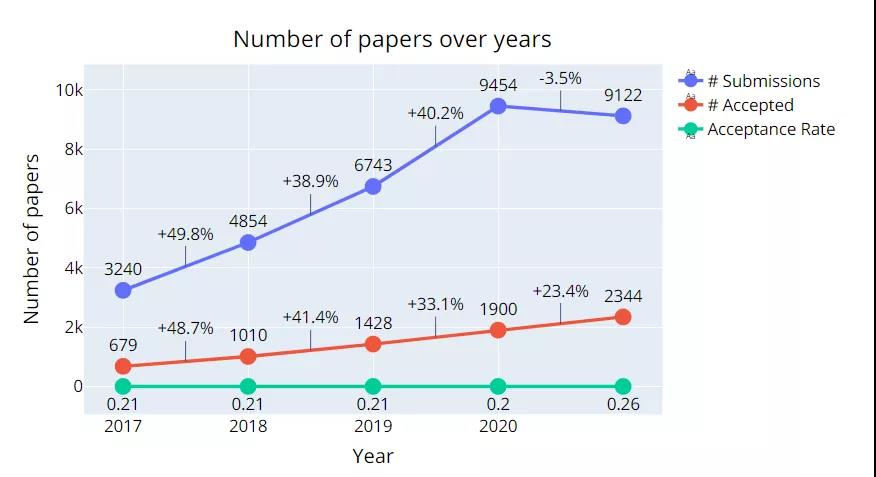
据大会官方统计,今年 NeurIPS 共有 9122 篇有效论文投稿,共接收 2344 篇,总接收率 26%,有 3% 被接收为 Spotlight 论文。相比去年,论文接收率稍高了一些,达到了 2013 年以来的最高水平。
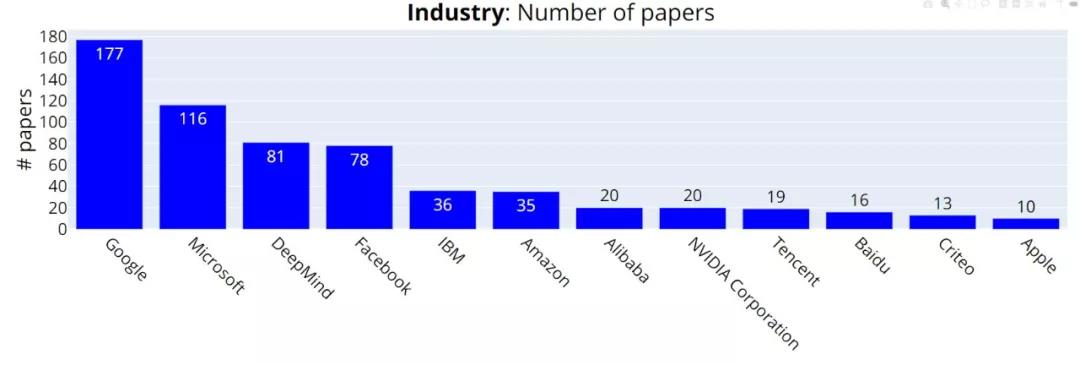
在投稿机构方面,NeurIPS 2021 中稿量(Accepted)排名前三的公司分别是谷歌(177 篇)、微软(116 篇)和 DeepMind (81 篇)。
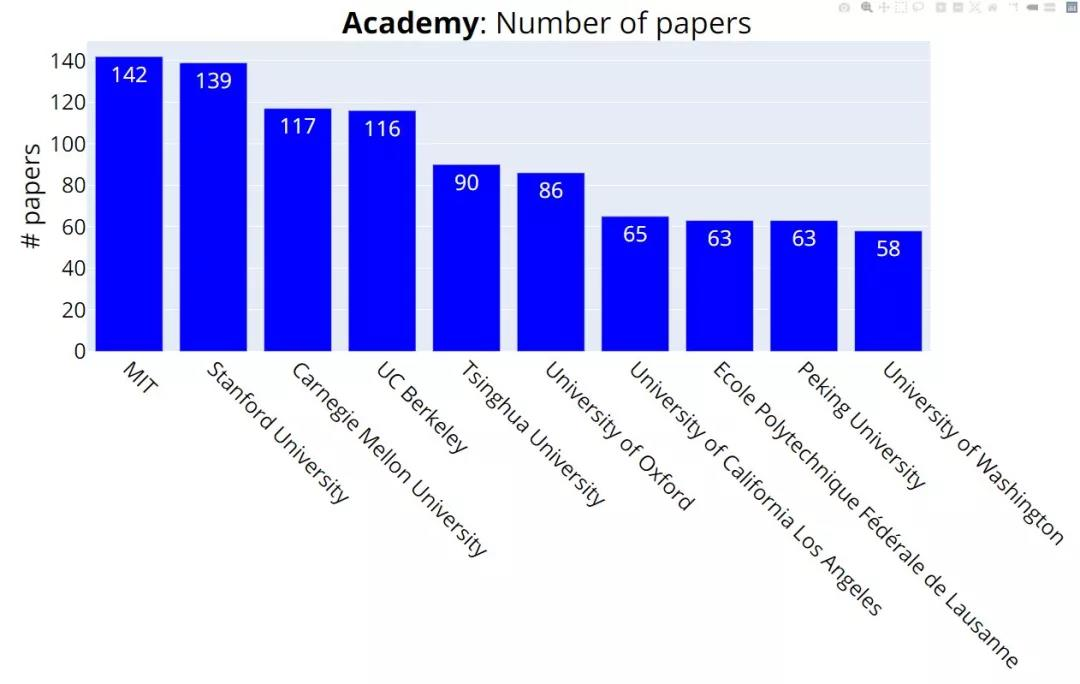
中稿量排名前三的学校分别是 MIT(142 篇)、斯坦福大学(139 篇)、CMU(117 篇)。加州大学伯克利分校以 1 篇之差(116 篇)排名第四。清华大学以 90 篇论文排名第五,北京大学以 63 篇论文排名第九。
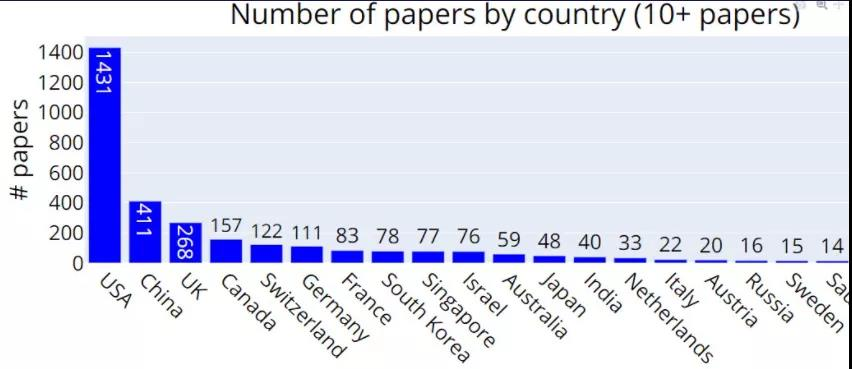
从国家 / 地区的角度看,中稿量排名前三的分别是:美国(1431 篇)、中国(411 篇)、英国(268 篇)。
下面让我们来看一下杰出论文奖、时间检验奖、数据集和基准 Track 最佳论文奖的获奖情况。
今年有六篇论文获选为杰出论文奖。分别由微软研究院、DeepMind 、谷歌、华盛顿大学 、巴黎科学艺术人文大学、魏茨曼科学研究所等机构研究者摘得。
获奖论文 1:A Universal Law of Robustness via Isoperimetry
获奖理由:本文提出了一个理论模型来解释为什么具有 SOTA 性能的深度网络比平滑拟合训练数据所需的参数更多。特别是,在关于训练分布的某些规律性条件下,O(1)-Lipschitz 函数在标签噪声尺度以下插值训练数据所需的参数数量为 nd,其中 n 是训练示例的数量,d 是数据的维度。这与传统结果形成了鲜明对比,传统结果表明一个函数需要 n 个参数来插值训练数据,为了平滑地插值,这个额外的因子 d 似乎是必要的。该理论简单而精炼,与经验观察到的模型大小一致,这些模型对 MNIST 分类具有较好的鲁棒泛化能力。这项工作还提供了关于为 ImageNet 分类开发稳健模型所需的模型大小的可测试预测。
获奖论文 2:On the Expressivity of Markov Reward
获奖理由:马尔可夫奖励函数是不确定性和强化学习下顺序决策的主要框架。本文详细、清晰地阐述了马尔可夫奖励能够使系统设计者根据他们对行为偏好或对状态、动作序列偏好来指定任务 。作者通过简单、说明性的例子证明,目前还存在一些无法指定马尔可夫奖励函数来引发所需任务和结果的任务。这一研究还表明,可以在多项式时间内(polynomial time)确定所需设置是否存在兼容的马尔可夫奖励,如果存在,说明也存在多项式时间算法可以在有限决策过程设置中构建这样的马尔可夫奖励。这项工作阐明了奖励设计存在的挑战,并且为研究马尔可夫框架何时以及如何实现人类所期望的性能开辟了新的道路。
获奖论文 3:Deep Reinforcement Learning at the Edge of the Statistical Precipice
获奖理由:科学进步离不开对方法进行严格比较。本文提出了切实可行的方法来提高深度强化学习算法比较的严谨性。该论文强调,在多项任务和多次运行中报告深度强化学习结果的标准方法可能使得评估新算法和先前算法是否一致或性能是否提高变得困难,研究者通过实证示例说明了这一点。该研究提出的性能概要旨在通过每个任务的少量运行进行计算,这对于计算资源有限的实验室来说是必要的。
获奖论文 4:MAUVE: Measuring the Gap Between Neural Text and Human Text using Divergence Frontiers
作者:Krishna Pillutla、Swabha Swayamdipta、Rowan Zellers、John Thickstun、Sean Welleck、Yejin Choi、 Zaid Harchaoui
机构:华盛顿大学 、艾伦人工智能研究院、斯坦福大学
论文地址:https://openreview.net/forum?id=Tqx7nJp7PR
获奖理由:该论文提出了一种比较模型生成文本分布与人类生成文本分布的散度度量方法 MAUVE。MAUVE 使用被比较的两个文本的量化嵌入的(软)KL 散度测量的连续族,这种度量方法的本质是对度量连续族的集成,旨在捕获 I 类 error(生成不切实际的文本)和 II 类 error(不捕获所有可能的人类文本)。该研究通过实验表明,与之前的散度指标相比,MAUVE 可以识别模型生成文本的已知模式,并且与人类判断的相关性更好。该方法将给开放端文本生成带来重要影响。
获奖论文 5:A Continuized View on Nesterov Acceleration for Stochastic Gradient Descent and Randomized Gossip
获奖理由:该论文提出了 Nesterov 加速梯度方法的「连续」版本,其中两个独立的矢量变量在连续时间内联合,这种方法很像使用微分方程理解加速的方法,不同的是使用梯度更新发生在泊松点过程决定的随机时间。这种新方法促成了一种(随机化)离散时间方法:(1)与 Nesterov 方法具有相同的加速收敛性;(2) 提供利用连续时间参数进行的清晰透明的分析,比之前对加速梯度方法的分析更容易理解;(3) 避免了连续时间过程离散化的额外错误,这与之前使用连续时间过程理解加速方法的几种尝试形成鲜明对比。
获奖论文 6:Moser Flow: Divergence-based Generative Modeling on Manifolds
作者:Noam Rozen、Aditya Grover、Maximilian Nickel、Yaron Lipman
机构:魏茨曼科学研究所、Meta(Facebook)AI、加州大学洛杉矶分校
论文地址:https://openreview.net/pdf?id=qGvMv3undNJ
获奖理由:本文提出了一种在黎曼流形上训练连续归一化流 (CNF) 生成模型的方法。该研究主要是利用 Moser (1965) 的结果,该结果使用具有几何规律性条件的受限 ODE 类来表征 CNF 的解,并使用目标密度函数的散度明确定义。该研究提出的 Moser Flow 方法使用这种解的概念发展了一种基于参数化目标密度估计的 CNF 方法。实验表明,与之前的 CNF 工作相比,该研究的方法训练时间更快,测试性能更出色。更普遍地,这种利用几何规律性条件来规避反向传播训练的概念可能会引起研究者更广泛的兴趣。
NeurIPS 2021 时间检验奖颁给了论文《Online Learning for Latent Dirichlet Allocation》。
这篇论文发表于 2010 年,论文作者是当时来自普林斯顿大学的 Matthew D. Hoffman、David M. Blei 和法国国家信息与自动化研究所的 Francis Bach。
论文地址:
https://proceedings.neurips.cc/paper/2010/file/71f6278d140af599e06ad9bf1ba03cb0-Paper.pdf
该论文提出了一种基于随机变分梯度的推理过程,用于在非常大的文本语料库上训练 LDA 模型。该论文通过理论证明了训练过程收敛到局部最优。令人惊讶的是,这种简单的随机梯度更新对应于证据下界(ELBO)目标的随机自然梯度。在实验方面,该论文首次表明 LDA 可以轻松地在数十万个文档的文本语料库上进行训练,使其成为解决「大数据」问题的实用技术。这个想法在 ML 社区产生了很大的影响,因为它为更通用的随机梯度变分推理过程提供了基础。在这篇论文之后,就不需要再使用完整的批训练过程进行变分推理了。
今年 NeurIPS 推出了新的奖项,即数据集和基准 Track 最佳论文奖 ,以表彰面向数据工作的研究。今年有两篇论文获得了该奖项,分别由加州大学洛杉矶分校、斯坦福大学的研究者摘得。
获奖论文 1:Reduced, Reused and Recycled: The Life of a Dataset in Machine Learning Research
获奖理由:本文分析了数千篇论文并研究了不同机器学习子社区中数据集使用的演变,以及数据集采集和创建之间的相互作用。该研究发现在大多数社区中,随着时间的推移,数据集的使用情况发生了演变,这些数据集来自少数机构。这种演变是有问题的,因为基准泛化会变差,放大数据集来源中存在的偏见,并且研究界更难接受新的数据集。这对整个机器学习社区来说需要提高警惕,让研究者更加批判性地来思考哪些数据集可用于基准测试,并让研究者更加重视创建新的、更多样化的数据集。
获奖论文 2: ATOM3D: Tasks On Molecules in Three Dimensions
作者:Raphael John Lamarre Townshend、Martin Vögele、Patricia Adriana Suriana、Alexander Derry、Alexander Powers、Yianni Laloudakis、Sidhika Balachandar、Bowen Jing、Brandon M. Anderson, Stephan Eismann、Risi Kondor、Russ Altman、Ron O. Dror
机构:斯坦福大学
论文地址:https://openreview.net/pdf?id=FkDZLpK1Ml2
获奖理由:本文介绍了一组基准数据集,其中包含小分子、生物聚合物的 3D 表示,涵盖单分子结构预测和生物分子之间的相互作用以及分子功能和设计工程任务。此外,该研究还将 3D 模型简单而强大的实现与具有 1D 或 2D 表示的 SOTA 模型进行基准测试,结果显示该数据集在低维对应物方面具有更好的性能。这项工作提供了如何为给定任务选择和设计模型的重要见解。该研究不仅提供了基准数据集,还提供了基线模型和开源工具来利用这些数据集和模型,大大降低了机器学习人员进入计算生物学和分子设计的门槛。
参考链接:https://blog.neurips.cc/2021/11/30/announcing-the-neurips-2021-award-recipients/
![]()
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com