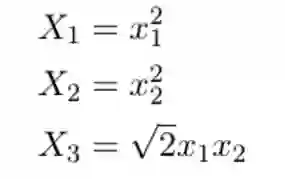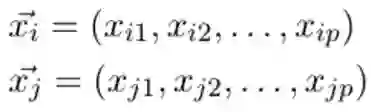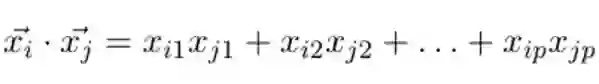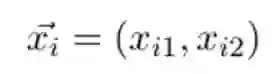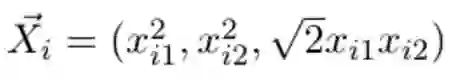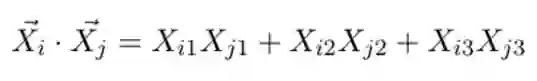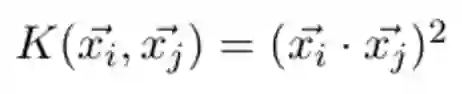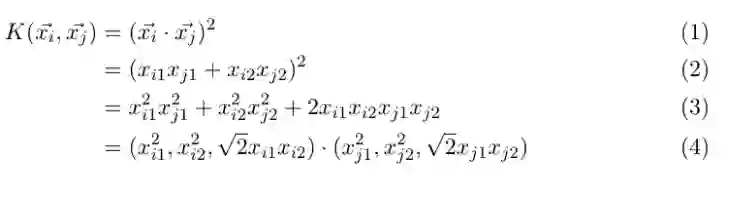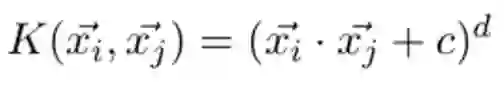从大间隔分类器到核函数：全面理解支持向量机

选自KDNuggets

机器之心编译

参与：刘晓坤、蒋思源

在这篇文章中，我们希望读者能对支持向量机（SVM）的工作方式有更高层次的理解。因此本文将更专注于培养直觉理解而不是严密的数学证明，这意味着我们会尽可能跳过数学细节而建立其工作方式的直观理解。

自从 Statsbot 团队发表了关于（时间序列的异常检测（time series anomaly detection）的文章之后，很多读者要求我们介绍支持向量机方法。因此 Statsbot 团队将在不使用高深数学的前提下向各位读者介绍 SVM，并分享有用的程序库和资源。

如果你曾经使用机器学习执行分类任务，应该会听说支持向量机（SVM）。这个算法的历史已经有五十出头，它们随着时间不断在进化，并适应于各种其它问题比如回归、离群值分析和排序等。

在很多深度学习开发者的模型储备中，SVM 都是他们的至爱。在 [24]7（https://www.247-inc.com/），我们也将使用它们解决多个问题。

我将更专注于培养直觉理解而不是严密的数学推导，这意味着我们会尽可能跳过数学细节而建立其工作方式的理论的直观理解。

 分类问题

假设你们的大学开设了一项机器学习课程，课程的讲师发现那些擅长数学或者统计学的学生往往表现的最好。课程结束之后，老师们记录了注册课程的学生的分数，他们对每一个学生根据其在机器学习课程上的表现加上了一个标签：「好」或者「坏」。

现在，老师们想要确定数学和统计学的得分与机器学习课程表现的关系。或许，根据他们的统计结果，他们会在学生注册课程时加上一个前提条件限制。

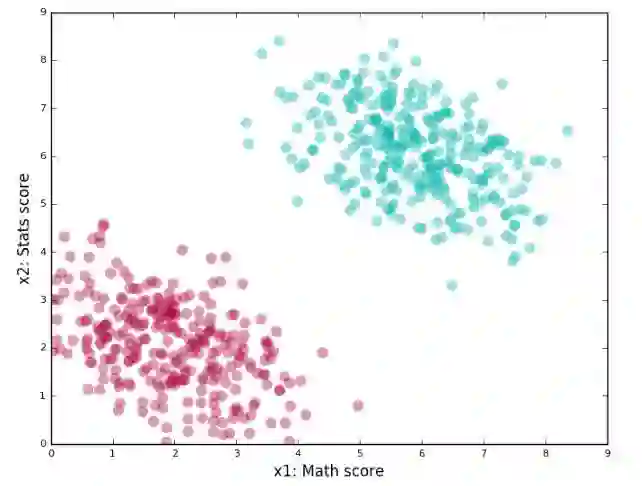
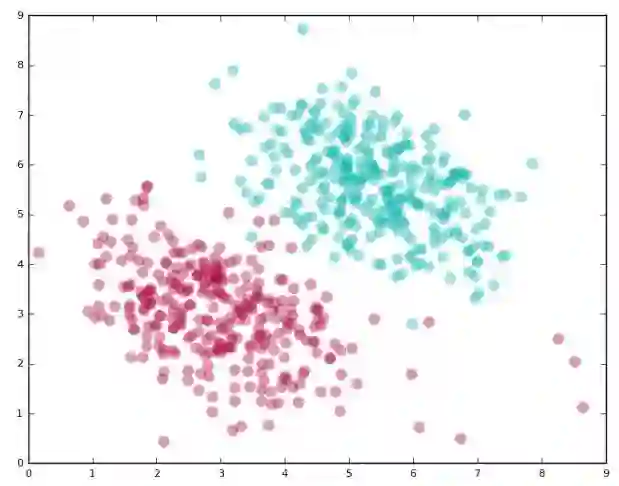
他们会怎么做呢？首先把他们的数据表示出来，我们可以画一个二维图，一个坐标轴表示数学成绩，另一个表示统计学成绩。每个学生的具体成绩作为一个点在图中表示。

点的颜色（绿色或者红色）表示学生在机器学习课程中的表现：「好」或者「坏」。将图画出来的话应该是这样的：

当一个学生要求注册课程的时候，讲师将会要求她提供数学和统计学的成绩。根据他们已有的数据，他们将对她在机器学习课程上的表现作出合理的猜测。我们真正想要的是一类以形式（math_score,stats_score）馈送到「分数元组」的算法。这个算法能告诉你一个学生在图中是以一个红点还是一个绿点表示（红/绿可理解为类别或者标签）。当然，这个算法已经以某种方式包含了训练数据的特征。

在这个案例中，一个好的算法将能寻找在红色和绿色群集之间的分界线（即决策边界），然后确定一个分数多元组将依赖于哪一侧。我们选择绿色方或者红色方的其中一侧作为他在这项课程中最可能的表现水平标签。

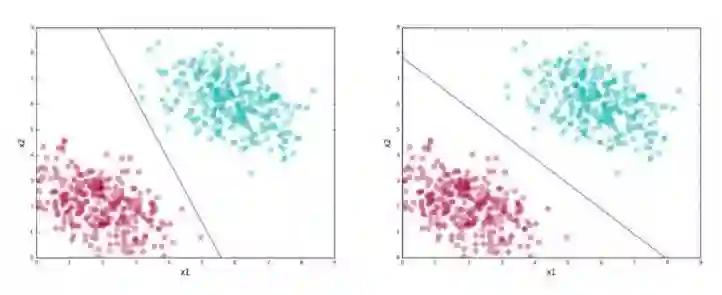
这条线称为决策边界（因为它将不同标记的群集分离开来）或者分类器（我们用它来将点集分类）。图中展示了这个问题中可能的两个分类器。

好分类器和坏分类器

有一个很有趣的问题：以上两条线都将红色和绿色的点群集分离开来。有什么合理依据能让我们选择其中一个而舍弃另一个吗？

要注意一个分类器的价值并不在于它能将训练数据分离的多好。我们最终是希望它能将尚未见过的数据分离（即测试数据）。因此我们需要选择能捕捉训练数据的普遍模式的那条线，而这条线更可能在测试数据中表现的更好。

以上所示的第一条线看起来有些许偏差，其下半部分看起来过于接近红点群集，其上半部分过于接近绿点群集。当然它确实很完美的将训练数据分离开来，但是如果在测试数据中遇到了有一个点离群集稍远的情况，它很有可能会将其加上错误的标记。

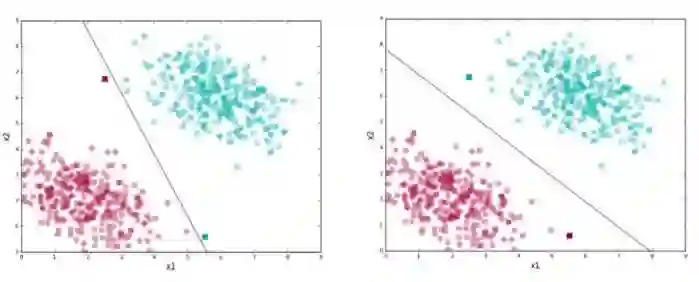
而第二的点就没有这样的问题。例如，下图为两个分类器分离方块点群集的结果展示。

第二条线在正确分离训练数据的同时也尽可能的远离两个群集，即采取最大间隔的策略。处于两个群集的正中间位置能降低犯错的风险，可以说，这给了每一个类的数据分布更多的浮动空间，因此它能更好的泛化到测试数据中。

SVM 就是试图寻找第二类决策边界的算法。上文我们只是通过目测选择更好的分类器，但实际上为了在一般案例中应用，我们需要将其隐含原理定义地更加精确。以下将简要说明 SVM 是如何工作的：

1. 寻找能准确分离训练数据的决策边界；

2. 在所有这些决策边界中选择能最大化与最近邻点的距离的决策边界。

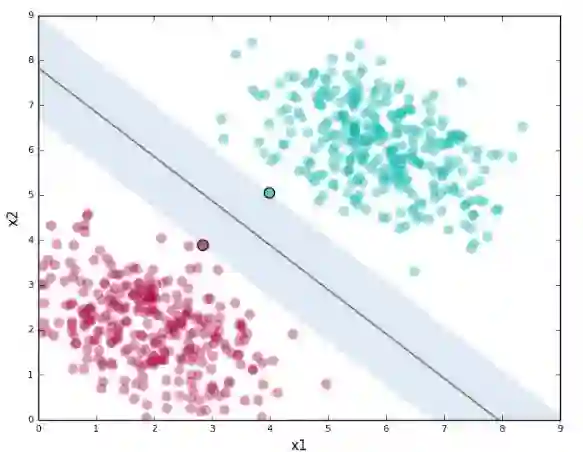
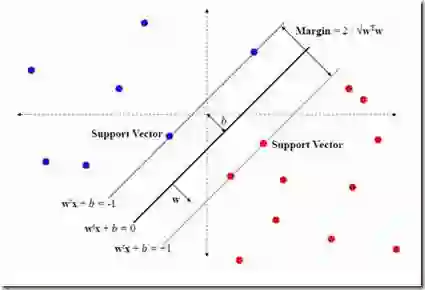
那些定义了这条决策边界的最近邻点被称作支持向量。而决策边界周围的区域被定义为间隔。下图展示了支持向量和对应的第二条决策边界：黑色边界的点（有两个）和间隔（阴影区域）。

支持向量机提供了一个方法在多个分类器中寻找能更准确分离测试数据的分类器。虽然上图中的决策边界和数据是处于二维空间的，但是必须注意 SVM 实际上能在任何维度的数据中工作，在这些维度中，它们寻找的是和二维空间决策边界类似的结构。

比如，在三维空间中它们寻找的是一个分离面（后面将简要提到），在更高维空间中它们寻找的是一个分离超平面，即将二维决策边界和三维分离面推广到任意维度的结构。一个可以被决策边界（或者在普遍意义上，一个分离超平面）被称作线性可分数据。分离超平面被称作线性分类器。

容错性和软间隔分类器

我们在上一节看到的是一个线性可分数据的简单例子，但现实中的数据通常是很凌乱的。你也很可能经常遇到一些不能正确线性分类的例子。这里展示了一个这样的例子：

很显然，使用一个线性分类器通常都无法完美的将标签分离，但我们也不想将其完全抛弃不用，毕竟除了几个错点它基本上能很好的解决问题。那么 SVM 会如何处理这个问题呢？SVM 允许你明确规定允许多少个错点出现。你可以在 SVM 中设定一个参数「C」；从而你可以在两种结果中权衡：

1. 拥有很宽的间隔；

2. 精确分离训练数据；

C 的值越大，意味着在训练数据中允许的误差越少。

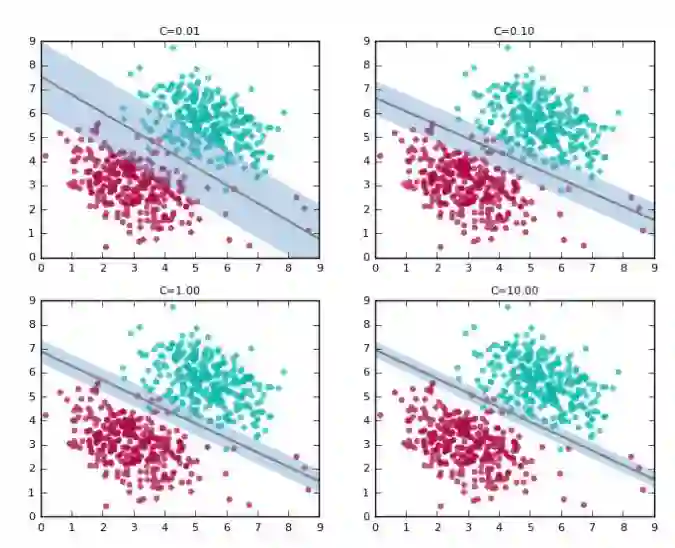
必需强调一下这是一个权衡的过程。如果想要更好地分类训练数据，那么代价就是间隔会更宽。以下几个图展示了在不同的 C 值中分类器和间隔的变化（未显示支持向量）。

注意决策边界随 C 值增大而倾斜的方式。在更大的 C 值中，它尝试将右下角的红点尽可能的分离出来。但也许我们并不希望在测试数据中也这么做。第一张图中 C=0.01，看起来更好的抓住了普遍的趋势，虽然跟更大的 C 值相比，它牺牲了精确性。

考虑到这是一个权衡方法，需要注意间隔如何随着 C 值的增大而缩小。

在之前的例子中，间隔内是不允许任何错点的存在的。在这里我们看到，同时拥有好的分离边界和没有错点的间隔是基本不可能的。由于现实世界中的数据几乎不可能精确的分离，确定一个合适的 C 值很重要且很有实际意义。我们往往使用交叉验证选择合适的 C 值。

线性不可分数据

我们已经介绍过支持向量机如何处理完美或者接近完美线性可分数据，那对于那些明确的非线性可分数据，SVM 又是怎么处理的呢？毕竟有很多现实世界的数据都是这一类型的。当然，寻找一个分离超平面已经行不通了，这反而突出了 SVMs 对这种任务有多擅长。

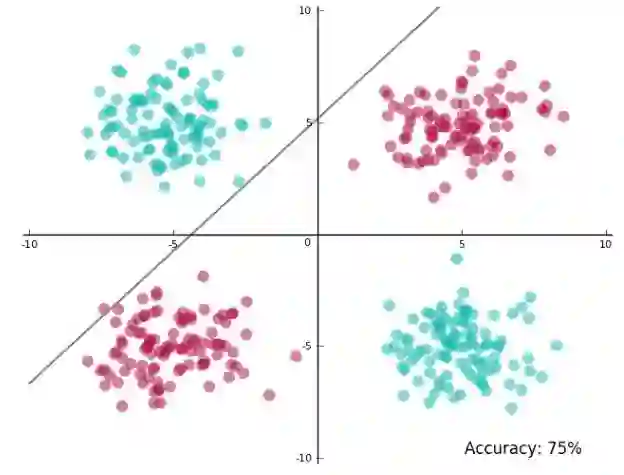
这里有一个关于线性不可分数据的例子（这是著名的异或问题变体），图中展示了线性分类器 SVM 的结果：

这样的结果并不怎么样，在训练数据中只能得到 75% 的准确率，这是使用决策边界能得到的最好结果。此外，决策边界和一些数据点过于接近，甚至将一些点分割开来。

现在轮到我最喜欢 SVM 的部分登场了。我们目前拥有：一项擅长寻找分离超平面的技术，以及无法线性分离的数据。那么怎么办？

当然是，将数据映射到另一个空间中使其线性可分然后寻找分离超平面！我会一步一步的详细介绍这个想法。

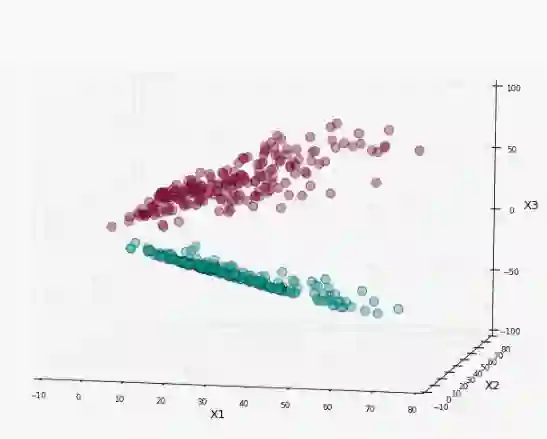
仍然从上图中的数据集为例，然后将其映射到三维空间中，其中新的坐标为：

下图中展示了映射数据的表示，你发现了能塞进一个平面的地方了吗？

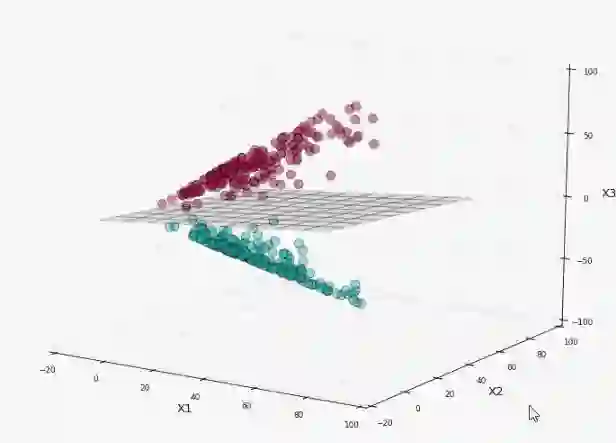
让我们开始在上面运行 SVM：

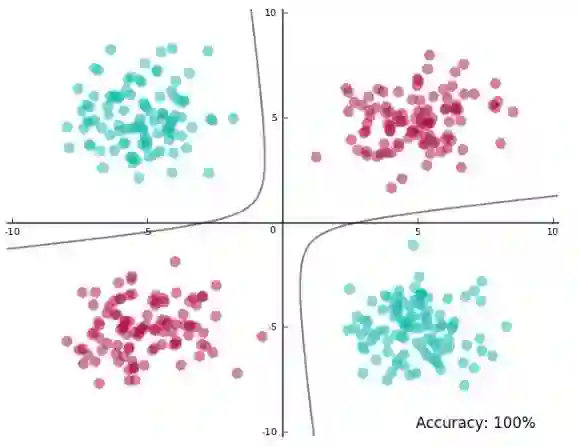
标签分离很完美，接下来将平面映射回初始的二维空间中看看决策边界是什么样子：

在训练数据中得到了 100% 的准确率，而且分离边界并不会过于接近数据点，太棒了！初始空间中决策边界的形状依赖于映射函数的形式。在映射空间中，分离边界通常是一个超平面。

要记住，映射数据的最主要的目的是为了使用 SVM 寻找分离超平面。

当将分离超平面映射回初始空间时，分离边界不再是一条线了，间隔和支持向量也变得不同。根据视觉直觉，它们在映射空间的形态是很好理解的。

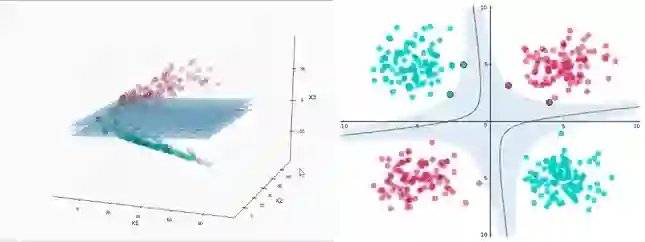
看看它们在映射空间中的样子，再看看在初始空间。3D 间隔（为了避免视觉混乱，没有加上阴影）是分离超平面之间的区域。

在映射空间中有 4 个支持向量，这很合理，它们分布在两个平面上以确定间隔。在初始空间中，它们依然在决策边界上，但是看起来数量并不足以确定最大间隔。

让我们回过头分析一下：

1. 如何确定要将数据映射到什么样的空间？

我之前已经很明确的提过，在某个地方出现了根号 2！在这个例子中，我想展示一下向高维空间映射的过程，因此我选了一个很具体的映射。一般而言，这是很难确定的。不过，多亏了 over』s theorem，我们能确定的是通过将数据映射到高维空间确实更可能使数据线性可分。

2. 所以我要做的就是映射数据然后运行 SVM？

不是。为了使上述例子更好理解，我解释的好像我们需要先将数据映射。如果你自行将数据映射，你要怎么表征无穷维空间呢？看起来 SVMs 很擅长这个，是时候看看算法的核函数了。

核函数

最终还是这个独家秘方才使得 SVM 有了打标签的能力。在这里我们需要讨论一些数学。让我们盘查一下目前我们所见过的：

1. 对于线性可分数据，SVM 工作地非常出色。

2. 对于近似线性可分数据，只要只用正确的 C 值，SVM 仍然可以工作地很好。

3. 对于线性不可分数据，可以将数据映射到另一个空间使数据变得完美或者几乎完美线性可分，将问题回归到了 1 或者 2。

首先 SVM 一个非常令人惊喜的方面是，其所有使用的数学机制，如精确的映射、甚至是空间的维度都没有显式表示出来。你可以根据数据点（以向量表示）的点积将所有的数学写出来。例如 P 维的向量 i 和 j，第一个下标区分数据点，第二个下标表示维度：

点积的定义如下：

如果数据集中有 n 个点，SVM 只需要将所有点两两配对的点积以寻找分类器。仅此而已。当我们需要将数据映射到高维空间的时候也是这样，不需要向 SVM 提供准确的映射，而是提供映射空间中所有点两两配对的点积。

重提一下我们之前做过的映射，看看能不能找到相关的核函数。同时我们也会跟踪映射的计算量，然后寻找点积，看看相比之下，核函数是怎么工作的。

对于任意一个点 i：

其对应的映射点的坐标为：

我们需要进行以下操作以完成映射：

• 得到新坐标的第一个维度：1 次乘法
  

• 第二个维度：1 次乘法
  

• 第三个维度：2 次乘法
  

加起来总共是 1+1+2=4 次乘法，在新坐标中的点积是：

为了计算两个点 i 和 j 的点积，我们需要先计算它们的映射。因此总共是 4+4=8 次乘法，然后点积的计算包含了 3 次乘法和 2 次加法。

• 乘法：8（映射）+3（点积）=11 次乘法
  

• 加法：2 次（点积之间）
  

总数为 11+2=13 次计算，而以下这个核函数将给出相同的结果：

首先在初始空间中计算向量的点积，然后将结果进行平方。把式子展开然后看看是否正确：

确实是这样。这个式子需要多少次计算呢？看看以上式子的第二步。在二维空间中计算点积只需要 2 次乘法和 1 次加法，平方运算是另一次乘法。因此，总计为：

• 乘法：2（初始空间的点积）+1（平方运算）=3 次乘法
  

• 加法：1（初始空间的点积）
  

总数为 3+1=4 次计算。只有之前计算量的 31%。

看起来使用核函数计算所需要的点积会更快。目前看来这似乎并不是什么重要的选择：只不过是 4 次和 13 次的比较，但在输入点处于高维度，而映射空间有更高的维度的情形中，大型数据集的计算所节省的计算量能大大加快训练的速度。因此使用核函数有相当大的优势。

大部分 SVM 程序库已经经过预包装并包含了一些很受欢迎的核函数比如多项式，径向基函数（RBF），以及 Sigmoid 函数。当不使用映射的时候（比如文中第一个例子），我们就在初始空间中计算点积，我们之前提过，这叫做线性核函数（linear kernel）。很多核函数能提供额外的手段进一步调整数据。比如，多项式核函数：

该多项式允许选择 c 和 d（多项式的自由度）的值。在上述 3D 映射的例子中，我使用的值为 c=0，d=2。但是核函数的优点远远不止于此！

还记得我之前提到向无穷维空间映射的情况吗？只需要知道正确的核函数就可以了。因此，我们并不需要将输入数据映射，或者困惑无穷维空间的问题。

核函数就是为了计算当数据确实被映射的时候，内积的形式。RBF 核函数通常在一些具体的无穷维映射问题中应用。在这里我们不讨论数学细节，但会在文末提到一些参考文献。

如何在空间维度为无穷的情况计算点积呢？如果你觉得困惑，回想一下无穷序列的加法是如何计算的，相似的道理。虽然在内积中有无穷个项，但是能利用一些公式将它们的和算出来。

这解答了我们前一节中提到的问题。总结一下：

1. 我们通常不会为数据定义一个特定的映射，而是从几个可用的核函数中选择，在某些例子中需要做一些参数调整，最后选出最适合数据的核函数。

2. 我们并不需要定义核函数或者自行将数据映射。

3. 如果有可用的核函数，使用它将使计算更快。

4. RBF 核函数可将数据映射到无穷维空间中。

SVM 库

你可以在很多 SVM 库中进行选择，并开始你的实验：

• libSVM
  

• SVM—Light
  

• SVMTorch
  

很多普适的机器学习库比如 scikit-learn 也提供 SVM 模块，通常在专用的 SVM 库中封装。我推荐使用经验证测试可行的 libSVM。

libSVM 通常是一个命令行工具，但下载包通常捆绑封装了 Python、Java 和 MATLAB。只要将你的数据文件经 libSVM 格式化后（下载文件中 README 将解释这一部分，以及其它可选项），就可以开始试验了。

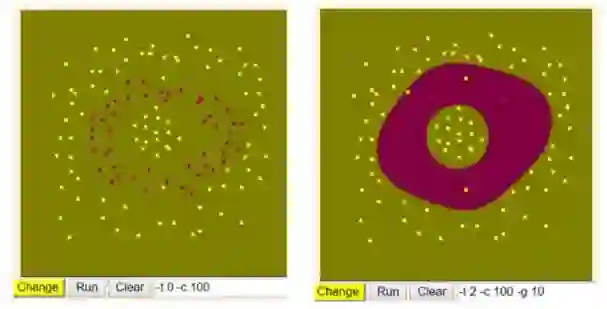
实际上，如果你想快速理解不同核函数和 c 值等如何影响决策边界，试试登陆「Graphical Interface」的 home page。在上面标记几类数据点，选择 SVM 参数，然后运行就可以了。我很快去尝试了一下：

我给 SVM 出了个难题，然后我尝试了几个不同的核函数：

网站界面并没有展示分离边界，但会显示 SVM 判断分类标签的结果。正如你所见，线性核函数完全忽略了红点，认为整个空间中只有黄点。而 RBF 核函数则完整的为红点划出了两个圈！

原文链接：http://www.kdnuggets.com/2017/08/support-vector-machines-learning-svms-examples.html

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者/实习生）：hr@jiqizhixin.com

投稿或寻求报道：content@jiqizhixin.com

广告&商务合作：bd@jiqizhixin.com