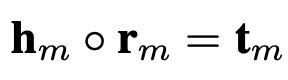AAAI 2020 开源论文 | 可建模语义分层的知识图谱补全方法

©PaperWeekly · 作者|蔡健宇
学校|中国科学技术大学
研究方向|知识图谱
论文链接:https://arxiv.org/abs/1911.09419
开源代码:https://github.com/MIRALab-USTC/KGE-HAKE

知识图谱与补全任务
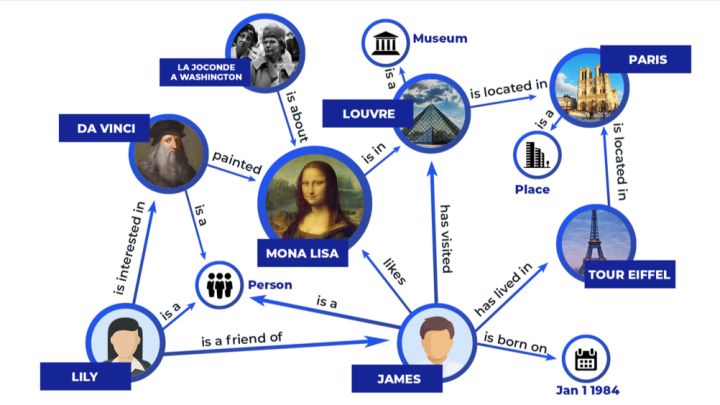

-
基于距离的模型 (Distance-based Models) -
双线性模型 (Bilinear Models) -
神经网络模型 (Neural Network Models)
 , 其中
, 其中  ,k
表示向量维度,它可以建模互逆关系与复合关系,却难以建模对称关系。
,k
表示向量维度,它可以建模互逆关系与复合关系,却难以建模对称关系。
 , 其中
, 其中  ,
, 表示向量间的 Hadamard 积,即
表示向量间的 Hadamard 积,即  ,它能够建模上述三种关系。
,它能够建模上述三种关系。
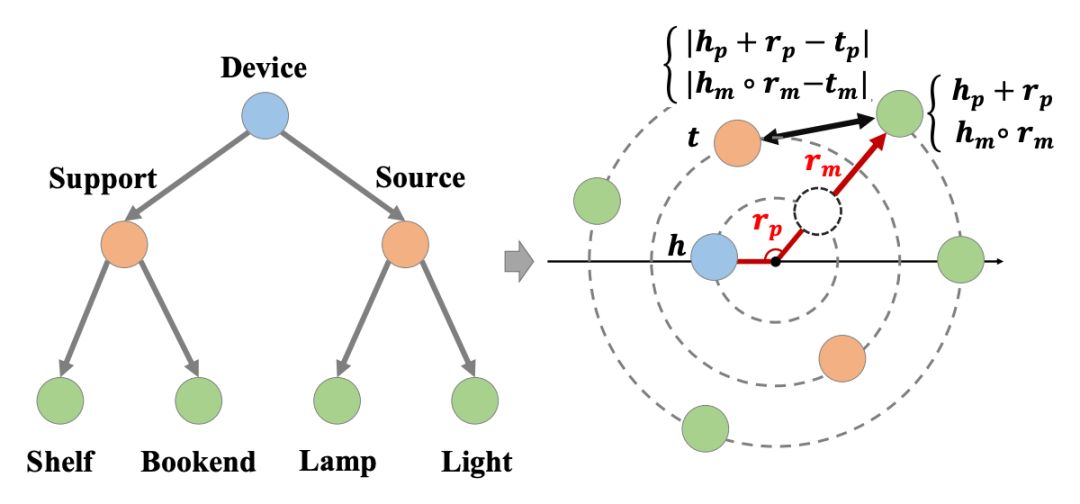
1. 语义分层现象
-
< 棕榈树 (palm),上位词 (_hypernym),树 (tree) > -
< 兰开斯特 (Lancaster),位于 (located_in),英格兰 (England) >
-
处于最高语义层级的实体对应着树的根节点 -
拥有更高的语义层级的实体更加接近根节点 -
语义层级更低的实体更加接近叶子节点 -
处于相同语义层级的实体到根节点的距离相同
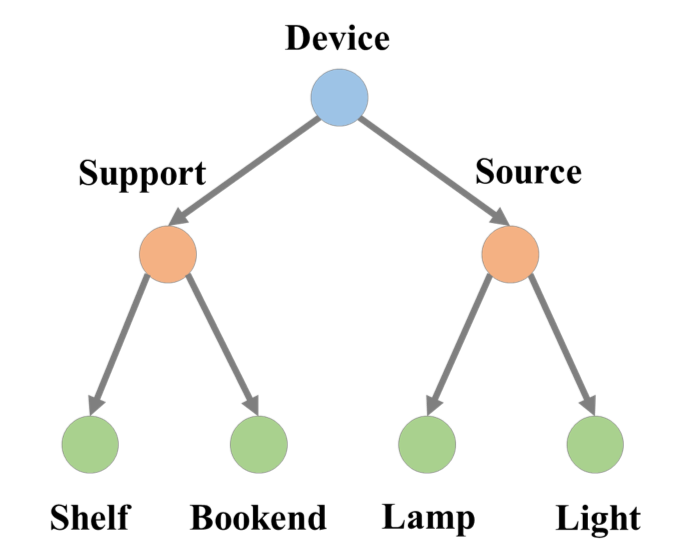
-
分属不同语义层级的实体,例如 <哺乳动物 (mammal)> 与 <狗 (dog)>;<奔跑 (run)> 与<移动 (move)>。 -
属于相同语义层级的实体,例如 <玫瑰 (rose)> 与 <牡丹 (peony)>;<卡车 (truck)> 与 <货车 (lorry)>。
2. HAKE 模型
-
模长部分用于建模分属不同层级的实体 -
角度部分用于建模属于同一层级的实体
2.1 模长部分
 与
与  分别为头实体、尾实体与关系向量,我们的建模如下:
分别为头实体、尾实体与关系向量,我们的建模如下:
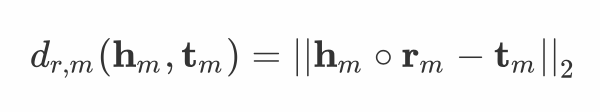
2.2 角度部分
 分别为头实体、关系与尾实体向量,我们的建模如下:
分别为头实体、关系与尾实体向量,我们的建模如下:
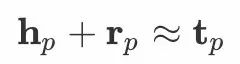
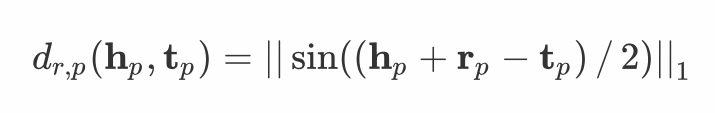
2.3 模长 + 角度
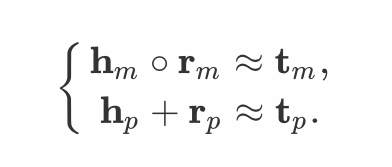
 、
、  与
与  分别表示综合后的头实体、关系与为实体向量。
分别表示综合后的头实体、关系与为实体向量。
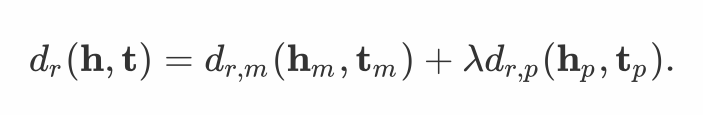
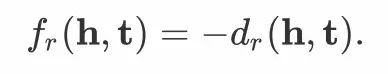
2.4 基准模型 ModE
3. 实验与分析
3.1 数据集
-
WN18RR,主要包含两种类型的关系:(a) 对称关系,如 _similar_to,该关系类型连接的头尾实体属于同一语义层级;(b) 非对称关系,如 _hypernym,该关系连接的头尾实体属于不同语义层级。 -
FB15k-237,包含的关系数量最多,关系类型最复杂,仅有部分关系表示语义层级。 -
YAGO3-10,该数据集和 FB15k-237 类似,包含许多具有高入度 (Indegree) 的关系,即在同一个关系下,一个头/尾实体可能对应着大量的尾/头实体。例如,(?,hasGender,male)(?,hasGender,male) 拥有超过 1,000 个正确的头实体,但这些头实体的含义却可能相差悬殊,因此建模难度更高。
3.2 实验结果
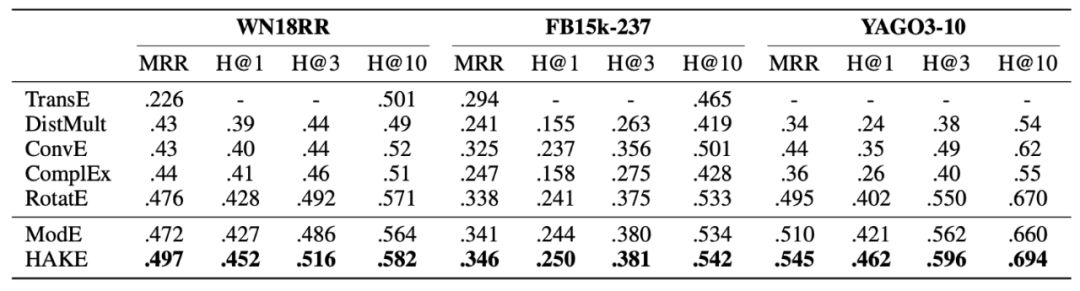
-
ModE 模型的参数量和 TransE 相同,且模型同样简单,但在各个数据集上的性能都远高于它; -
HAKE 模型在各个数据集上的表现都显著优于现有的最佳模型。
3.3 可视化分析
3.3.1 关系的可视化分析
(i) 关系的模长部分
-
位于更高语义层级的实体更加靠近树的根节点,故模长更小 -
位于更低语义层级的实体更加靠近树的叶节点,故模长更大
-
如果头实体的语义层级更高,而尾实体的语义层级更低,那么我们期望 -
如果头实体的语义层级更低,而尾实体的语义层级更高,那么我们期望 -
如果头尾实体位于相同的语义层级,那么我们期望
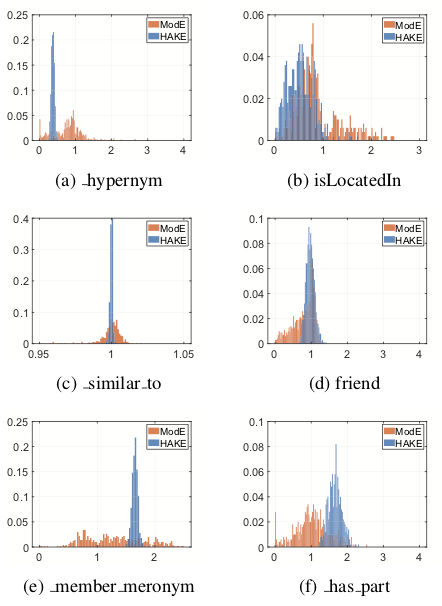
这样的实验结果与上述猜想完全一致。我们还发现,与 ModE 相比,HAKE 的模长嵌入向量的取值分布更为集中,方差更小,这表明 HAKE 能够更加清晰准确地对语义层级进行建模。
(ii) 关系的角度部分
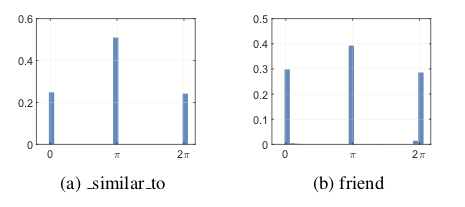
3.3.2 实体可视化分析
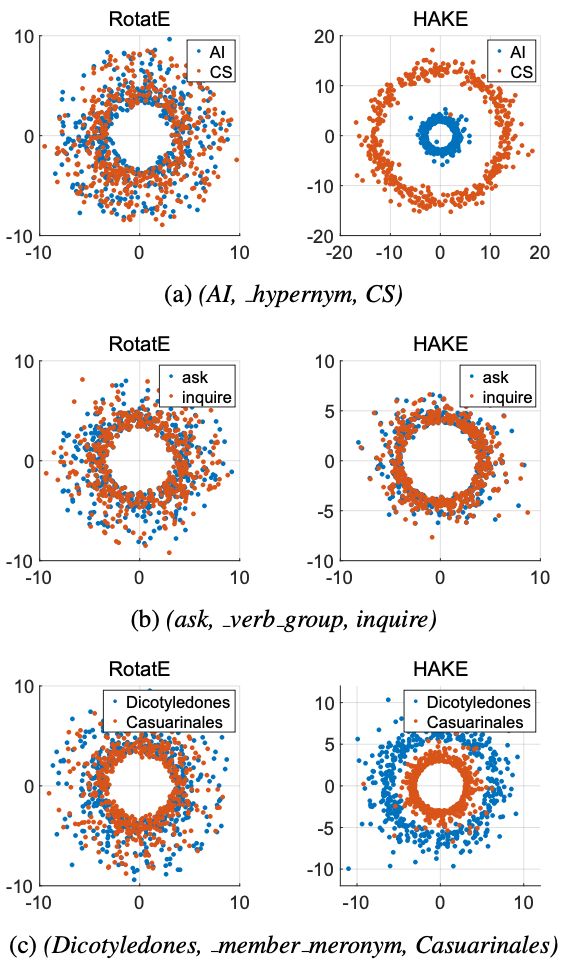
本文介绍了一个可建模语义分层的知识图谱补全模型:HAKE。该模型使用极坐标系对语义分层进行建模。其中,模长部分用于建模分属不同语义层级的实体;角度部分用于建模属于相同语义层级的实体。实验结果表明 HAKE 的性能优于现有的性能最好的方法。进一步分析结果显示,训练得到的模型中模长与角度的表现与预期相符,能够很好地对语义层级进行建模。
点击以下标题查看更多往期内容:

让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
▽ 点击 | 阅读原文 | 下载论文 & 源码