国内首次！3位清华姚班00后学霸斩获计算机理论顶会最佳学生论文奖

---

  新智元报道  

编辑：Joey 好困

【新智元导读】2022年计算机理论顶会STOC正式开幕，来自清华姚班的三位00后学霸斩获最佳学生论文奖。

近日，理论计算机科学领域顶级国际会议第54届ACM计算理论年会（STOC 2022）拉开帷幕。

清华姚班的三位00后学霸范致远、李嘉图与杨天祺，凭借着「伪随机函数的精确复杂性与计算复杂性理论中自举现象的黑盒自然证明障碍」夺得最佳学生论文奖。

从左至右分别为范致远、李嘉图和杨天祺（来源：中国科学报）

ACM计算理论年会（STOC）是理论计算机科学领域最顶级的国际会议，在整个计算机科学领域享有崇高的声望，并被公认属于难度最高的会议之一。它与IEEE计算机科学基础年度研讨会（FOCS）并称理论计算机科学两大顶会。

STOC由ACM SIGACT（Special Interest Group in Algorithms and Computation Theory）主办，涵盖的领域包括算法和数据结构、计算复杂性、密码学、计算几何、组合学、随机与去随机化、算法博弈论和量子计算等。

2022年的STOC共收到457篇投稿，录用135篇，接收率约为29%。 然后再从中评选出2篇最佳论文奖，以及2篇最佳学 生论文奖。 这么算下来的话，获奖率仅为2.9%。

获得最佳论文奖的2篇论文，分别来自魏茨曼科学研究所、希伯来大学，以及莫斯科国立大学。

获得最佳学生论文奖的2篇论文，分别来自麻省理工学院、微软研究院，以及清华大学。

演讲地址：https://www.youtube.com/watch?v=QcBypyG6oMU

6月23日，正是这三人获奖论文的汇报时间。

论文地址：https://dl.acm.org/doi/abs/10.1145/3519935.3520010

伪随机函数(pseudorandom functions)是无法与随机函数区分开的函数族。它作为密码学许多构造的起点，是密码学的基础。因此构造高效的伪随机函数在理论及应用中有多种意义。

论文研究了伪随机函数的电路复杂性，在多个重要的电路复杂性类中对伪随机函数给出了紧的上界与下界。例如证明了在一般电路中，若多项式大小的电路可计算的伪随机函数存在，则存在一个仅需大约2n个门的电路族即可计算的伪随机函数。同时，该研究无条件地证明了计算任何伪随机函数至少需要2n-2个门。

00后学霸：从保送清华到顶会获奖

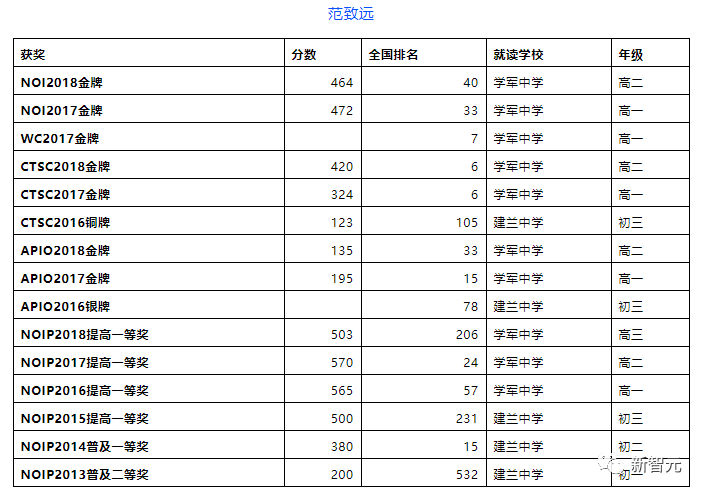
范致远

范致远曾是南京一中大名鼎鼎的「化学一哥」，从初三第一次接触化学实验开始，范致远就对化学产生了浓厚的兴趣，他在化学上的才华逐渐「显山露水」。

进校后几次考试，他的化学成绩都非常突出。

参加中国化学奥林匹克竞赛决赛之前，范致远曾和省队的伙伴们一起在南京大学接受了化学系老师们的系统赛前培训，他在4个月内「攒下200页错题集」。

2015年，范致远在中国化学奥林匹克竞赛（决赛）暨冬令营中获得了金牌，获得了清华大学化学生物基础科学班一本线录取资格。

2017年7月30日，范致远在第34届全国青少年信息学奥林匹克竞赛中拿到金牌，清华大学也向他抛来了「橄榄枝」。

范致远成功获得了清华大学化学生物基础科学班一本线录取资格。

来看看大神满满的获奖经历。

再看看范致远曾经就读的杭州学军中学，两次获世界冠军，获国际金牌3枚，亚太地区金牌29枚、全国金牌23枚，全国联赛一等奖259人次。

近十年来，录取清北人数达七八十人，其学生遍布哈佛、麻省理工、斯坦福等国际名校，就职于谷歌、Facebook、微软、百度等著名IT企业。

说成「清北的摇篮」也不过分。

李嘉图

李嘉图高中就读于太原五中，18年7月，李嘉图同学在第35届全国青少年信息学奥林匹克竞赛中斩获金牌，进入国家集训队，同时获得保送清华大学资格。

2018年1月29日至2月1日举办的「清华大学全国优秀中学生信息学冬季体验营」中，清华大学计算机系面向全国知名高中邀请了「213名优秀信息学奥赛学生」参加体验营。

李嘉图是山西省唯一一位获邀参加体验营的同学。

杨天祺

高中就读于南京师范大学附属中学，曾获2018年全国青少年信息学奥林匹克联赛（省级赛区）一等奖、2018年全国青少年信息学奥林匹克竞赛一等奖。

2019年入选信息学国家集训队，并获得清华保送资格。研究兴趣是计算复杂性，目前专注于电路下限。

那么这样三位来自全国各地的天才少年，是怎样组建团队并成功夺得最佳学生论文的呢？

事实上，这篇论文从一开始的构思，到研究团队的组建再到成功发表获奖，其过程并不是一帆风顺。

在《中国科学报》的一篇采访中，李嘉图表示，他们三人并非一开始就在一个团队。

这篇论文最初的理念雏形由李嘉图和杨天祺二人提出。

大一下学期开始，他们在姚期智院士讲授的计算机应用数学课程中收获颇丰，并提前选修了段然老师的计算理论课程。这门课程，让他了解到计算复杂性领域还有许多值得深耕的领域。

那段时间里，他们一起翻看了近些年电路复杂性理论的一个重要突破，即麻省理工学院教授Ryan Williams提出的，证明电路复杂度下界（circuit lower bound）的算法方法（algorithmic approach）。

李嘉图说，「我们想要从一个电路复杂度理论的前沿问题入手，了解这个领域的背景、主要技术，以及目前的重要问题」。

不过，实际进展并没有想象那么轻松。经过对该领域的一番研究后，二人虽然大致明白了这一理论的框架，但并未发现值得他们研究的选题。

这时范致远的加入，如「及时雨」一般，为后续研究指出了一个大概的方向。

范致远说，「我们三个人的合作氛围很舒服，大家经常交流和探讨，思想会碰撞出很多火花。后来，我们对原方法进行了大幅度的简化和改进，而且用完全不同的技术探索了这一问题的更多侧面」。

范致远的加入为团队的研究进展提供了全新的动力，相关研究成果也紧接着喷涌而出。

在论文的终稿里，最初预设的问题已经不是最终的结果，最后论文的展示也取得成功，即在三个模型中证明了上下界。

值得一提的是，李嘉图和杨天祺的另一篇论文也被STOC 2022接收了。

论文地址：https://dl.acm.org/doi/10.1145/3519935.3519976

演讲地址：https://www.youtube.com/watch?v=54ILPK6JK5c

电路复杂性（circuit complexity）是复杂性理论中广为关注的问题。其中一个经典结论是大多数语言都需要指数级大小的电路才足以进行判定，但是该结论的证明是非构造性的。给出一个需要很大的电路才能判定的具体语言是有几十年历史的开放问题。

在此之前，最好的结果是Find, Golovnev, Hirsch, and Kulikov于2016年给出的：存在一个多项式可计算的语言不能被(3+1/86)n-o(n)大小的电路计算。该研究改进了他们的方法，证明了同一个语言不能被3.1n-o(n)大小的电路计算。

清华姚班：计算机领域天才的摇篮

清华学堂计算机科学实验班，也就是「姚班」。

因为由2000年图灵奖获得者、美国国家科学院院士姚期智创办，得名「姚班」

姚班致力于培养与美国麻省理工学院、普林斯顿大学等世界一流高校本科生具有同等、甚至更高竞争力的领跑国际拔尖创新计算机科学人才。

本届STOC接收的135篇论文里，有7篇出自姚班师生。

而在历届STOC的论文展演中，姚班学子也是常客。如2020年就有4篇，2021年有3篇。

上一个获STOC最佳学生论文奖的中国人是陈立杰，他也是姚班学子中的一员，他目前麻省理工学院深造。

姚班在计算机领域的地位可想而知。

截至2021年12月，姚班学生在本科期间发表的论文有358篇记录在册，姚班学生为论文通讯作者或主要完成人的有277篇，并有121人次在FOCS、STOC、SODA、NIPS、COLT、CVPR、AAAI、ICLR等国际顶级会议上作大会报告。

参考资料：

https://www.tsinghua.edu.cn/info/1175/94548.htm

新闻来源：

https://mp.weixin.qq.com/s/ttwfftwpYGBV-NsIfcCX7Q