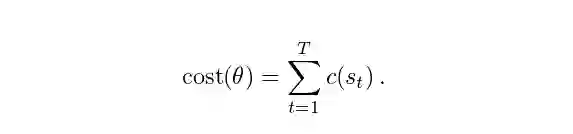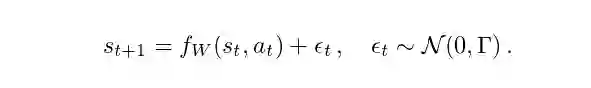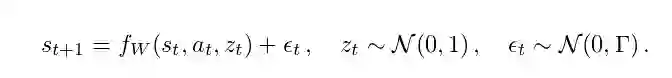全新强化学习算法详解，看贝叶斯神经网络如何进行策略搜索

2017 年 7 月 25 日 机器人圈

图：pixabay

原文来源：medium

作者：José Miguel Hernández Lobato

「机器人圈」编译：嗯~阿童木呀、多啦A亮

首先，在这里，介绍一下我们最近在ICLR（International Conference on Learning Representations）上发表的论文《利用贝叶斯神经网络进行随机动力系统中的学习与策略搜索》（ICLR 2017）。点击此处查看论文代码和视频。它介绍了一种基于模型的强化学习的新方法。这项成果的主要作者是Stefan Depeweg，他是慕尼黑技术大学的博士生。

在这项成果中，关键的贡献在于我们的模型：具有随机输入的贝叶斯神经网络，其输入层包含输入特征，以及随机变量，其通过网络向前传播并在输出层转换为任意噪声信号。

随机输入使我们的模型能够自动捕获复杂的噪声模式，提高基于模型的模拟质量，并在实践中制定出更好的策略。

问题描述

我们解决了随机动力系统中策略搜索的问题。例如，我们要操作诸如燃气轮机这样的工业系统：

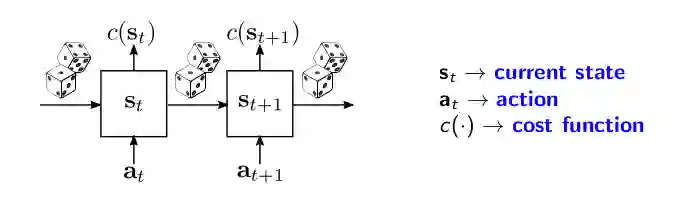
这些系统的抽象图如下所示。系统的当前状态被表示为s_t并且与每个状态s_t相关联，同时存在一个由函数c（•）给出的成本c（s_t）。在每个时间步中，我们应用一个操作，这将在下一个时间步s_t + 1时影响系统的状态。

从s_t到s_t + 1的转换不仅仅是由action a_t决定的，而且还由一些我们无法控制的噪声信号决定。该噪声信号可由图中的骰子来表示。在涡轮机示例中，噪声源自于我们观察到的包括传感器测量的状态，这是对系统真实状态的不完整描述。

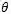
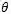
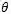
为了控制系统，我们可以使用策略函数a_t =π（s_t; ）将当前状态s_t映射到action a_t中。例如，π（•; ）可以是一个具有权重的神经网络。

我们的目标是找到一个策略（具有值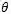），它将在状态轨迹序列上产生平均低成本函数值。例如，我们的目标是最小化预期：

需要注意的是，上述表达式是随机的，因为它取决于初始状态s_1的选择和状态转换中的随机噪声。

批量强化学习

我们考虑批量强化学习场景，在学习过程中不会与系统交互。这种情况在现实世界的工业环境中是很常见的，例如涡轮机控制，其中探测受到限制，以避免产生可能的系统损失。

因此，为了找到一个最优策略，我们只需要从已经运行的系统中以状态转换的形式获得一批数据D = {(s_t, a_t, s_t+1)}，而且我们将无法收集任何额外的数据。

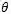
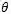
首先，我们需要从D，一个p（s_t + 1 | s_t，a_t）的模型中进行学习，也就是将下一个状态s_t + 1的预测分布作为当前状态s_t和应用的action a_t的函数。然后，我们将该模型与策略相结合，以便得到p（s_t + 1 | s_t，a_t =π（s_t;）），其描述了当使用策略π（•）进行控制时系统的演化。

以前的分布可以用于执行状态轨迹的roll-out或模拟。我们从随机采样状态s_1开始，然后从p（s_t + 1 | s_t，a_t =π（s_t;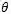））中进行迭代采样，以获得状态s_1，...，s_T的轨迹。

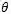
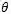
然后可以在采样的s_1，...，s_T中对成本函数进行评估，以近似成本（）。这种近似的梯度可以用于随机优化和在各个方向上进行移动，从而产生平均较低值的成本（）。

噪声在最优控制中的作用

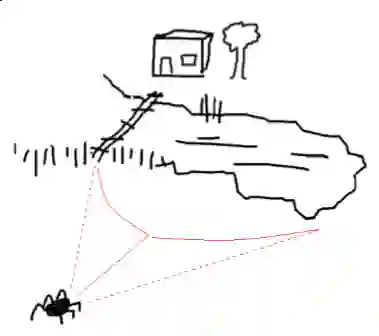
最优策略会受到状态转换中噪声的显著影响。关于这一点，Bert Kappen 在《最优控制理论的路径积分与对称破缺》中提出的醉酒蜘蛛故事可进行以很好的说明，在这里，我们可以将其用作一个激励示例来进行说明。

蜘蛛要回家的话，它有两个可能的路径：穿过湖上的桥或者绕着湖边走回家。在没有噪音的情况下，桥梁是比较好的选择，因为它更短。然而，在大量饮酒后，蜘蛛的运动可能会随机地左右随摇晃。考虑到桥梁狭窄，且蜘蛛不喜欢游泳，所以现在较优的选择是沿着湖边走回家。

显然，这个例子显示了噪声是如何显著地影响最佳控制的。例如，最优策略可以根据噪声水平的高低进行改变。因此，我们期望在基于模型的增强学习中获得显著的改进，通过捕获状态转换数据中存在的任何噪声模式。因此，我们期望通过高精度捕获状态转换数据中存在的任何噪声模式，从而获得基于模型的强化学习的显著改进。

具有随机输入的贝叶斯神经网络

实际上，状态转换数据中的大多数建模方法只是假设s_t + 1中的附加高斯噪声（additive Gaussian noise），即，

其中f_W可以视作一个权重为W的神经网络。在这种情况下，以最大似然法来学习W是非常容易的。然而，在现实世界的设置中附加高斯噪声的假设不太可能存在。

不过，可以通过在f_W中使用随机输入，从而在转换动力学中获得一个更为灵活的噪声模型。实际上，我们可以假设：

在这个模型下，输入噪声变量z_t可以通过f_W以复杂的方式进行变换，以在s_t + 1中产生任意的随机模式来作为s_t和a_t的函数。

然而，现在由于z_t是未知的，所以不能再以最大似然法来学习W。不过，我们可以采用一个相反思想的解决方案：贝叶斯方法，W和z_t进行后验分布。这个分布捕捉我们在看到D中数据后可能会采用的值的不确定性。

如果想要计算准确的后验分布其实是很棘手的，但我们可以学习高斯近似。这种近似的参数可以通过最小化对真后验的发散来调整。变异贝叶斯（VB）是一种通用于此类问题的方法，可以通过最小化Kullback-Leibler散度来实现。

α发散最小化（α-divergence minimization）

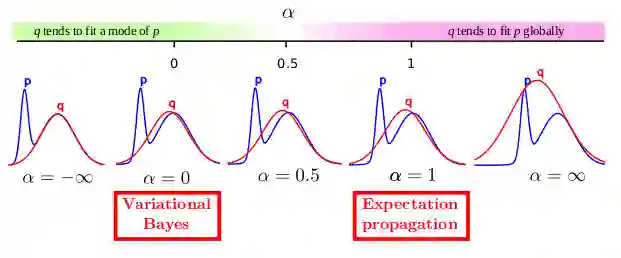
其实，对于如何学习因式分解后的高斯近似，我们可以通过最小化α发散来实现，而不使用VB。关于α发散，在Minka, Thomas P所著的《散度度量和消息传递》和我与Li Y.等人所著的《黑箱α发散的最小化》中皆有所提及。通过改变这种发散中的α值，我们可以在真实的后验分布p模式下进行平滑的插值，也可以在p中覆盖多种模式，如下图所示：

其实很有趣的一点是，VB是α发散最小化中α= 0的一种特殊情况。而另外一种众所周知的用于近似贝叶斯推理的方法是期望传播（expectation propagation），它可以由α= 1获得。在我们的实验中，我们使用α= 0.5，因为在实际情况下，这会产生更好的概率预测。关于这一点，《黑箱α发散的最小化》（ICML 2016）中有更为详尽的阐述。

示例的结果演示

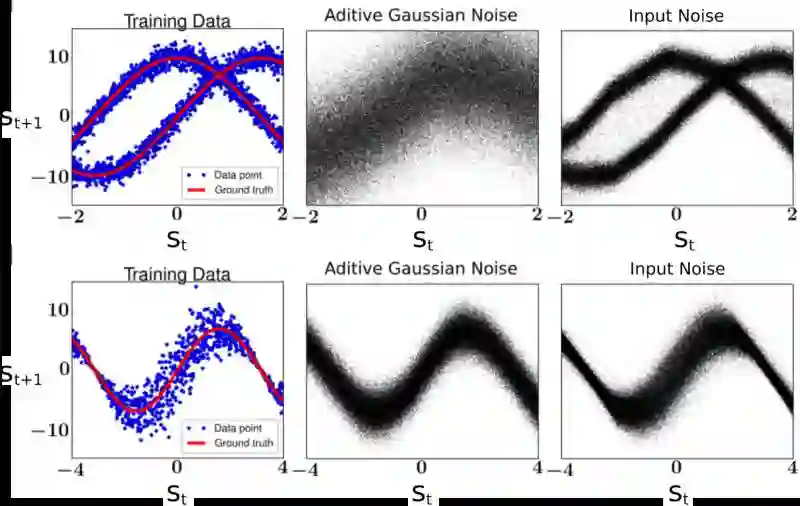
下图显示了在两个示例中进行具有随机输入的贝叶斯神经网络的执行结果。每个示例的训练数据显示在最左边的列中。顶行显示的是双模态预测分布的问题。底行显示的是异方差噪声的问题（噪声幅度取决于输入）。

中间列显示的是从仅使用附加高斯噪声的模型中所获得的预测。该模型无法捕获数据中的双重模式或异方差。最右边的列显示了具有随机输入的贝叶斯神经网络的预测，其可以自动识别数据中存在的随机模式的类型。

“落水鸡”问题的测试结果

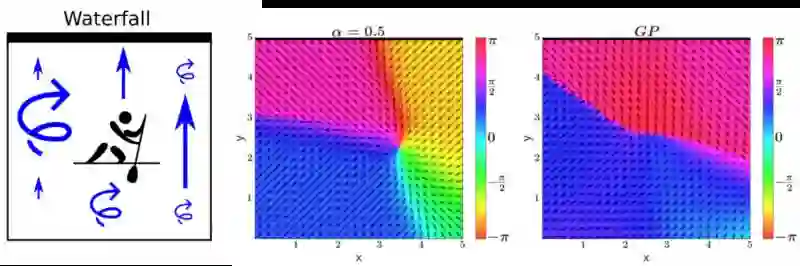
我们现在考虑一个强化学习基准，其中一个划独木舟在二维的河上划桨，如下图最左边的地图所示。在一个漂流的河中，将划独木舟推向位于顶部的瀑布，漂移在右边更强，左边更弱。如果独木舟落下瀑布，他必须在河底重新开始。

河流中也有扰动，左侧变强，右侧较弱。独木舟越接近瀑布获得的奖励越多。因此，他会想要靠近瀑布，但不要太近，以免翻船。这个问题叫做“落水鸡”，因为它与斗鸡有相似之处。

湍流和瀑布将使落水鸡成为一个高度随机的基准：瀑布下降的可能性在状态转换中引发双重态势，而不同的湍流引入异方差。

图中间的情节可以看出使用我们的贝叶斯神经网络随机输入的策略。这是一个几乎最优的策略，其中独木舟分子试图停留在x≃3.5和y≃2.5的位置。

右图显示了使用刚刚假设加性高斯噪声的高斯过程（GP）模型发现的策略。所产生的策略在实践中表现非常差，因为GP无法捕获数据中存在的复杂噪声模式。

工业基准评估结果

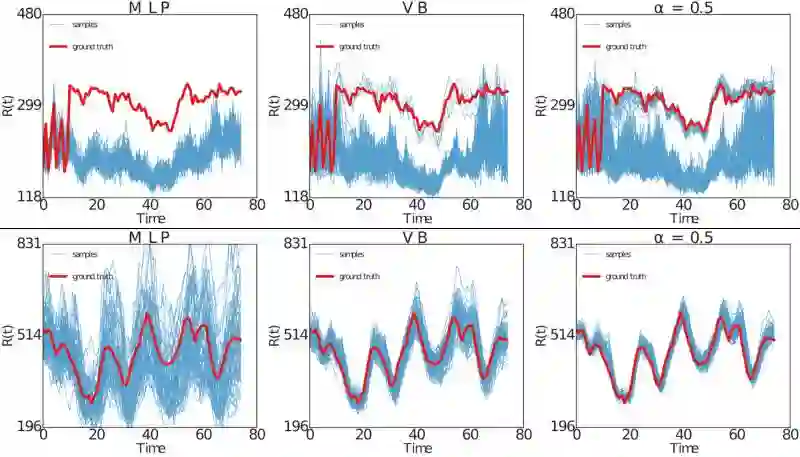
我们还使用称为“工业基准”的工业系统模拟器对实验中随机输入的贝叶斯神经网络的性能进行评估。作者认为：“工业基准”的目标是在某种意义上是现实的，它包括我们发现在工业应用中至关重要的各个方面。

下图显示，对于固定的动作序列，使用与1）多层感知器相对应的模型产生的roll-out，该多层感知器假定加性高斯噪声（MLP）和我们的贝叶斯神经网络训练2）变异贝叶斯（VB）或3 ）α分散最小化，α= 0.5。模拟的轨迹显示为蓝色，“工业基准”产生的地面实况显示为红色。

这个数字清楚地显示了用随机输入和α发散最小化的贝叶斯神经网络产生的roll-out是如何更接近地面真实轨迹。

结论

我们已经看到，在学习最优策略时，重要的是要考虑到过渡动态中复杂的噪声模式。我们具有随机输入的贝叶斯神经网络是用于捕获这种复杂噪声模式的最先进的模型。通过α＝0.5α的发散最小化，我们能够在这样的贝叶斯神经网络中执行精确的近似推理。这使得我们可以生成可用于学习更好策略的逼真的基于模型的模拟。

进一步阅读

在《隐变量贝叶斯神经网络的不确定性分解》（arXiv:1706.08495）中，我们研究了具有随机输入的贝叶斯神经网络预测中不确定性的分解。不确定性源于a）由于有限的数据（认识论不确定性）缺乏关于网络权重的知识，或b）对网络的随机输入（偶然的不确定性）。在《具有潜在变量的贝叶斯神经网络中的不确定性分解》（arXiv:1706.08495）中，我们展示了如何将这两种类型的不确定性与应用程序分开进行主动学习和安全强化学习。

我们推荐Alex Kendall的优秀的博客文章，此文介绍了上述两种计算机视觉深层神经网络的不确定性。

欢迎加入