这三个博弈论新趋势，正深刻影响深度强化学习

作者 | Jesus Rodriguez
编译 | 亚尔曼•佩皮
校对 | 丛末 & Camel
编辑 | 唐里

博弈论在现代人工智能（AI）解决方案中正扮演着至关重要的角色，深度强化学习（DRL）正是积极拥抱博弈论的头等公民。

从单智能体程序到复杂的多智能体深度强化学习环境，博弈论原理贯穿了 AI 程序的整个生命周期。而反过来，DRL 的快速演化也重新激发了人们对博弈论研究的关注。

目前，大多数 DRL 模型事实上还停留在传统的博弈论层面，例如纳什均衡或零和游戏等。但随着DRL的发展，传统博弈论方法已经逐渐呈现出不足之处，而同时则有一些新的博弈论方法被纳入到人工智能的程序当中。

因此，对于我们来说，若想进一步优化深度强化学习的模型，考虑融入新的博弈论方法，是值得考量的一个方向。

以下三个，正是在深刻影响 DRL 的「新」博弈论方法，或许用到你的模型中会大大改观模型的性能。

一、平均场博弈（Mean Field Games）

在博弈论家族中，平均场博弈（MFG）还是一个相对较新的领域。

平均场博弈论诞生于 2006 年，这一理论是由两个团队独立提出的，一个是蒙特利尔的 Minyi Huang、Roland Malhame 和 Peter Gaines，另一个是巴黎的 Jean-Michel Lasry和菲尔兹奖获得者 Pierre-Louis Lions。

从概念上讲，平均场博弈论是一套方法和技术的组合，它被用来研究由「理性博弈方」组成的大群体下的差异化博弈。这些智能体不仅对自身所处的状态（如财富、资金）有偏好，还关注其他智能体在整个样本分布中所处的位置。平均场博弈理论正是针对这些系统对广义纳什均衡进行了研究。

平均场博弈的经典案例是，如何训练鱼群朝相同方向游，或者以协作方式游。

这个现象很难用理论解释，但它的本质事实上是，鱼会根据最靠近的鱼群的行为做出反映。再具体点儿，每条鱼并不在乎其他单个鱼的行为，而是关注附近作为一个整体、统一移动的鱼群做出的行为。

如果我们用数学方程表述这个原理，一方面可以用 Hamilton-Jacobi-Bellman 方程来描述鱼对周边鱼群的反应，另一方面则可以用 Fokker-Planck-Kolmogoroy 方程来表示决定整个鱼群行动的所有鱼的行为集合。

平均场博弈理论就是这两个等式的组合。

从深度强化学习的角度来说，在研究大范围环境中 大量智能体的表现方面，平均场博弈论扮演着重要的角色。

实验和理论已经证实，在“接近无限多智能体、并假设采用不精确的概率模型进行操作”的环境中，已有的 DRL的方法并不具备现实可用性。

而 MFG 却是模拟这类 DRL 环境的一个有意思的方法，非常值得尝试。

一家叫做Prowler 的创业公司最近就在针对平均场博弈论（MFG）在大型多智能体（DRL）环境中的表现开展研究工作。

二、随机博弈（Stochastic games）

随机博弈可追溯到 20 世纪 50 年代，它由诺贝尔经济学奖获得者 Lloyd Shapley 提出。

理论上随机博弈的规则是，让有限多个博弈者在有限个状态空间中进行博弈，每个博弈者在每个状态空间都从有限个行为中选出一个行为，这些行为的组合结果会决定博弈者所获得的奖励，并得出下一个状态空间的概率分布。

随机博弈的经典案例是哲学家的晚餐问题：n+1 位哲学家（n 大于等于 1）围坐在一个圆桌周围，圆桌中间放了一碗米饭。每两位邻座的哲学家之间会放一支筷子以供这两位取用。因为桌子是圆形的，筷子的数量与哲学家的数量一样多。为了从碗中取到东西吃，哲学家需要同时从两边各取一支筷子组成一双，因此，在一位哲学家吃东西时，他的两位邻座就无法同时进食。哲学家的生活简单到只需要吃和思考，而为了存活下来，哲学家需要不断地思考和吃东西。这场博弈的任务就是设计出一个可以让所有的哲学家都活下来的制度。

DRL 已经开始应用随机博弈理论解决多玩家游戏问题。在许多多玩家游戏中，AI 智能体战队需要评估如何通过与其他智能体协作和竞争以最大化正向结果。

这一问题一般被称作探索-利用困境。在 DRL 智能体中构建随机博弈动态机制，可以有效地平衡 DRL 智能体在探索能力和利用能力方面的发展。DeepMind 在训练 AI 掌握 Quake III 游戏的工作中，就融合了一些随机博弈论中的概念。

三、进化博弈（Evolutionary Games）

进化博弈理论（EGT）是从达尔文进化论中得到的启发。

EGT 的起源可以追溯到 1973 年，当时 John Maynard Smith 和 George R.Price两人采用「策略」分析将演化竞争形式化，并建立数学标准，从而来预测不同竞争策略所产生的结果。

从概念上来说，EGT 是博弈论在进化场景中的应用。在这种博弈中，一群智能体通过重复选择的进化过程，与多样化的策略进行持续交互，从而创建出一个稳定的解决方案。

它背后的思路是，许多行为都涉及到群体中多个智能体间的交互，而其中某一个智能体是否获得成功，取决于它采取的策略与其他智能体的策略如何交互。

经典博弈论将关注点放在静态策略上，即参与者采取的策略不会随着时间改变，而进化博弈与经典博弈论不同，它关注策略如何随着时间演化，以及哪个动态策略是进化进程中最成功的那一个。

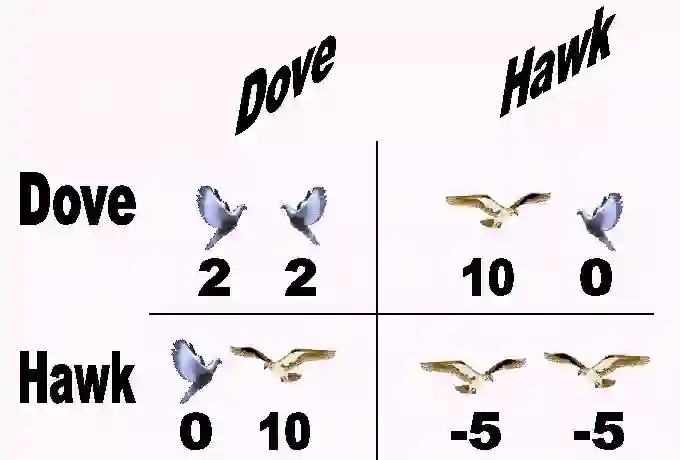
EGT 的经典案例是鹰鸽博弈（Howk Dove Game），它模拟了鹰与鸽之间对可共享资源的竞争。博弈中的每个竞争者都遵循以下两种策略之中的一种：

• 鹰：本能的强势，充满侵略性，除非身负重伤，否则绝不退却。

• 鸽：面对强势进攻会立即逃跑。

如果假设：

1）两个同样强势进攻的鹰进行搏斗，两者之间必然会发生冲突，且两者都很有可能受伤；

2）冲突的代价是每人都受到一定程度的损伤，用常量 C 表示这个损失；

3）如果鹰与鸽相遇，鸽会立刻逃跑，而鹰则会占有资源；

4）两只鸽相遇，则他们将公平地分享资源。鹰鸽博弈的对应收益可以用以下矩阵总结：

EGT 看上去似乎是特地为 DRL 环境而设计的。

在多智能体的 DRL 环境中，智能体在彼此交互的过程中会周期性地调整自己的策略。而 EGT 正是一种可以高效模拟这些交互的方法。最近，OpenAI 就展示了经过这种动态训练的智能体在玩捉迷藏游戏时的表现（https://openai.com/blog/emergent-tool-use/）。

via https://towardsdatascience.com/new-game-theory-innovations-that-are-influencing-reinforcement-learning-24779f7e82b1

---

点击“阅读原文”查看 AI 领域博弈论入门