为何努力了却没有成功？失败动力学或许能带来答案

我们总被成功的风光吸引，企图从成功的案例中找到可复制的路径，对“失败”的认识却不够清晰。近日，美国西北大学凯洛格商学院、复杂系统研究中心副教授王大顺等人在预印本平台上发布了新论文 Quantifying dynamics of failure across science, startups, and security。在该论文中，研究者阐述了失败的动力学机制。从动力学所得到的早期信号中“明察秋毫”，或许胜败早有伏笔。

来源  公众号“集智俱乐部”

作者  Leo

编辑  王怡蔺

我们是焦虑的，我们对成功亦有执念。面对如此庞大的“成功需求”，市面上的“成功学”书籍可谓汗牛充栋。然而成功的道路并非一帆风顺，福特在创办他的福特汽车之前破产过两次；J.K.罗琳的哈利波特书稿被出版社拒绝过十二次；更不要说“中学生作文中的老朋友”——爱迪生，在发明灯泡的过程中，他为了找到可以长时间点亮的灯丝经历了千余次的失败。

虽然我们都知道“失败是成功之母”这句格言，然而，我们对于失败的理解却少之又少。近日，美国西北大学凯洛格商学院、复杂系统研究中心副教授王大顺等人发表了最新的论文，开创性地阐述了失败的动力学机制。

论文题目：

Quantifying dynamics of failure across science, startups, and security

论文地址：

https://arxiv.org/abs/1903.07562

三个有关“成败”的大型数据集

为了完成这项研究，研究者们使用了三个异常巨大的数据集：

• NIH Grants

  1985 年至 2015 年期间，提交给美国国家卫生研究院（National Institutes of Health，NIH）的所有与健康有关的科研经费申报。因为美国国家卫生研究院是世界上最大的生物医学研究领域的资助者，因此在 1985 年至 2015 年期间，该机构提供收到了来自  139,091 名研究者的 776,721 份经费申报数据，并附有经费申报成功与否的信息。研究者能通过整理申报者的历次经费申报信息，从而提取出在经历多次失败最终获得成功的“生物医学研究员奋斗史”。

  
  

• Startups

  由美国风险投资协会（National Venture Capital Association）提供的 VentureXpert 数据库，包含了从 1970 年至 2016 年，由 253,579 名创业者创办的 58,111 个公司的数据。同样，通过这些数据研究者可以重建创业者的历次创业经历，并将创业成功定义为：进行 IPO 或被大公司收购。

  
  

  注：首次公开募股（Initial Public Offerings，简称IPO）是指一家企业或公司 第一次将它的股份向公众出售（首次公开发行，指股份公司首次向社会公众公开招股的发行方式）。

  
  

• Terrorist Attacks

  记录了 1970 年至 2017 年间的 3,178 个恐怖组织策划的 170,350 起恐怖袭击事件。这项数据来自于全球恐怖主义数据库（Global Terrorism Database，GTD）。把袭击成功定义为造成了至少一人的死亡；无人伤亡则表示袭击失败。

运气与学习

通常，我们认为一件事情的成功还是失败主要归功于运气（Chance）和学习（Learning）。研究者利用以上三个数据库检验这两项假说是否可靠。

运气模型

如果运气是成功与否的关键因素，也就意味着一件事情完全是由概率决定的。比如说，做一个事情成功的概率和抛硬币正面朝上的概率一样都是 0.5，那么多抛几次，得到正面朝上的机会（至少有一次是正面的概率）就会增加。

这种事情，做一次尝试和做一百次尝试都是一样的，所以第一次尝试的成功概率会等于倒数第二次尝试的成功概率（最后一次表示事情最终终于成功了）。且如图所示，失败曲线（Failure Streak）会完全吻合指数函数的图像。

运气模型以及对应的失败曲线，左侧表示的是首次尝试和倒数第二次尝试的概率，右侧表示的是多次失败的互补累积分布（CCDF）。

学习模型

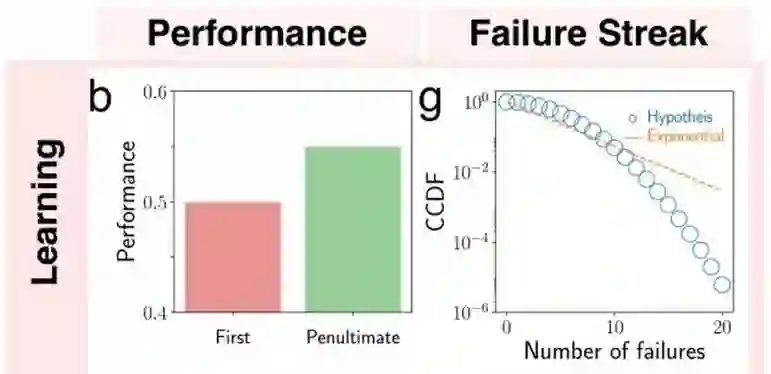
如果，事情的参与者能够从先前的失败中学习经验教训，那么后续尝试的成功概率会就会大为增加，换句话说，和第一次尝试相比，倒数第二次尝试的失败可能性会降低。就函数图象而论，失败曲线的“尾部”会比指数函数的尾部要“窄”。

学习模型的表现图示，以及对应的失败曲线。左侧表示的是首次尝试和倒数第二次尝试的概率，右侧表示的是多次失败的互补累积分布（CCDF）。

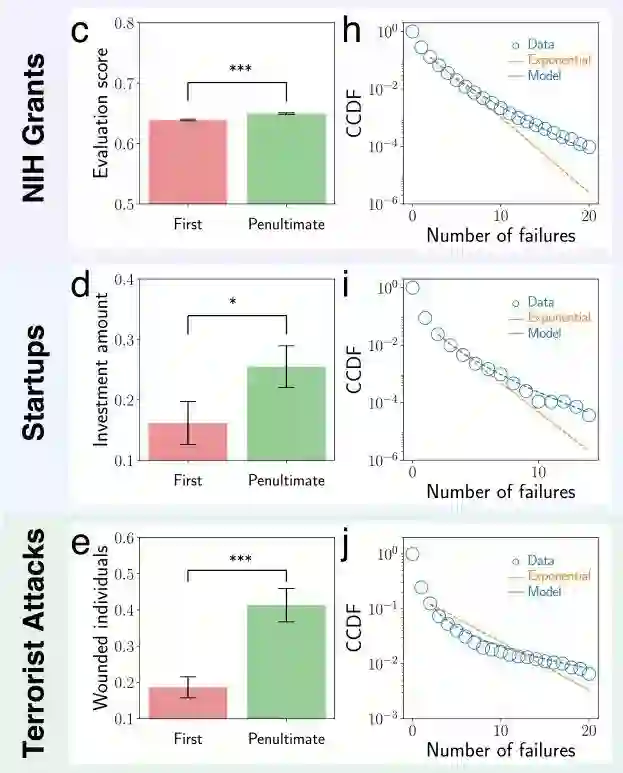
但是，当研究者用以上两种假说去表述先前提到的三个数据集中的真实案例数据时，研究者发现，实际的失败曲线的尾部比指数图像的尾部还要宽一些。显然，单一的运气和学习模型都无法解释人为何会成功和失败。或许，是这二者共同作用才造就了最后的结果。

NIH Grants、Startups、Terrorist Attacks三个数据集真实案例所反映出的表现结果与失败曲线

建立新模型

那么，“失败”到底受到了怎样的影响呢？研究者从一个简易的单变量模型入手研究失败的动力学机制。

尝试与部件

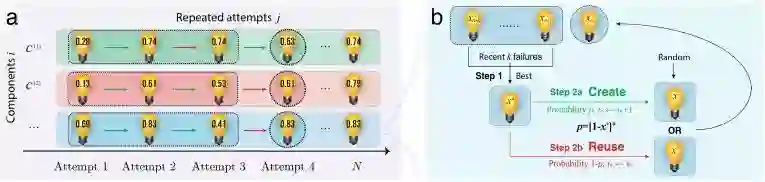
尝试、部件及其更迭模式，左图表示一个包含多个部件的事情，如何经过多次尝试之后，每个部件的分数均得到提升的过程；右图表示创造新部件还是沿用就部件的决策过程。

如上图 a 所示，首先，研究者假设，每一次尝试都包含了不同的部件（component）。例如以申报研究经费为例：申报一次生物医学研究经费（尝试）需要计算预算、编写数据管理规划、预估研究影响等等部件。在本研究中假设这些要素的分数 x 是独立无权的（权重为 1）。分数越高，该次部件也越可能成功。

当经历过一次失败，再做一次尝试的时候，参与者对其中的每一个部件的处理方法是：

1. 以概率 p 创造一个新的（图 a 中的绿色箭头）。

2. 以概率 1-p 沿用过去最好的版本 x*（图 a 中的红色箭头）。

参见上图 b，在评估这些部件分数的时候是随机给出一个 0 到 1 的数值（由运气决定是否成功）。但是考虑到实际情况。人们在给出一个新版本的部件时，会考虑到先前部件的质量——创造新版本的动力（概率 p）被设定为与 1-x* 单调相关。换句话说，如果过去做的最好的结果（x*）越差，人们越有动力去改进它。同时，在研究者的模型设计中，每多设计一个新的部件都要多花费一个单位的时间。

这个思路类似于游戏打怪升级装备，游戏玩家在购买、升级新的游戏装备的时候，不是土豪任性，随意氪金。而是会根据已有的装备能力进行选择：还不错的装备会留着继续用， 越烂的装备越有可能被替换掉。而打造更强大的游戏装备也是要花费时间的。

故此，研究者为模型设定了一个单一的表示学习数量变量 k。该模型称之为：k 模型（The k model）。

k 模型

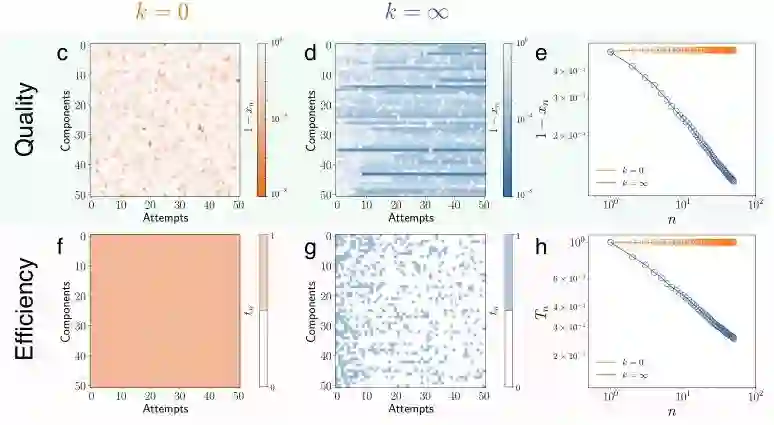
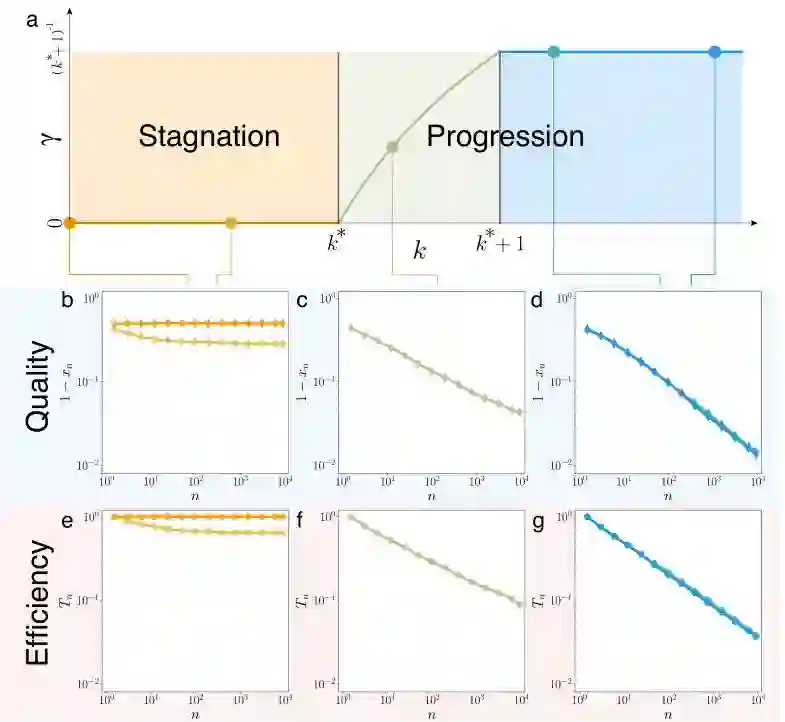
k 模型（The k model），从质量和效率两个角度来评估两种极端的k模型的结果。

当 k 等于 0 时（图中以橙黄色标识），意味着做出新尝试的人不考虑过去的尝试，每一次新的尝试都与过去的尝试无关。这时模型就退化为了运气模型。

当 k 趋近于 ∞ 时（图中以蓝色标识），意味着要考虑过去所有的尝试。我们可以用这个模型来估计失败动力学的时间尺度——学得越多越能节省时间。

同时，研究者也评估了两件指标，每次尝试的质量和效率。在 k=0 这样的运气模型中，反复尝试并不能带来总体质量和效率上的提高改进（图 c、f），最后的成功与否完全取决于撞大运。而在另一个模型中（图 d、g），因为有经验的积累，我们明显能够看到质量（评价分数 x，图中以 1-x 减小表示质量增高）与效率（T）的改进。

三级相变与临界的魔力

一个新的疑问是：从“啥都不学”到“学习一切”这个变化是一个渐进的过程么？或者说，k 值的变化能带来成功概率连续的改变么？

由两个阈值点带来的三级相变过程，只有当k值大于一定的临界值时，学习才能有效果。

根据研究者的研究表明，学习的程度是存在阈值的——学习对失败的影响被限定在了一定的范围内。换而言之，随着 k 从 0 增大到 ∞，在相当长对的一段时间内，因为学习的经验太少（k太小），学习的质量和效率都很低，学了跟没学效果一样（图 a 中的橙色部分）。但是，超过了一定的范围，我们也会发现，失败的动力学特征和 k=∞ 时，基本相同。也表明，只要学习的内容涵盖了足够多的尝试经验，其结果跟学习过往所有的经验差不过。

就此，我们发现失败的动力学是一个存在两个阈值点的三级相变过程。

举例来说，也许两个人的学习能力相差不大，但恰好处于临界值的两侧最后的学习质量和学习效率都相距甚远。超过临界状态的人能从过去的学习中受益，但恰恰低于临界状态的人却几乎是止步不前。

位于临界状态两侧的学习效果实例

关于失败的四种预测

基于上述的模型分析，研究者提出了四种预测，并在他们的数据集中进行了测试。

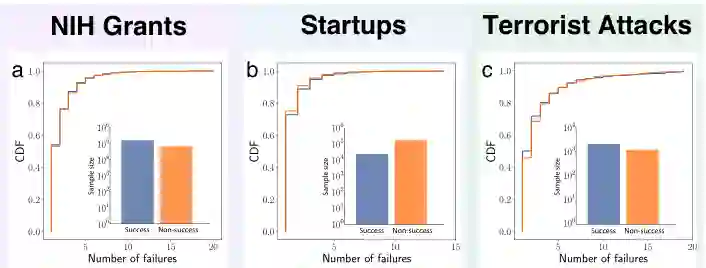
• 预测一 ：不是所有的失败都能带来成功。

成功组（蓝色）和非成功组（橙色）失败次数的互补累积分布（CCDF）

如图我们可见，在三个领域中都存在这一部分人一直无法获得成功。且每个领域中、每个失败次数的细分类别中，成功与不成功的比例也几乎一致。或许，当有一天我们获得了成功时，不要忘了我们身后那些锲而不舍却又屡战屡败的人们。

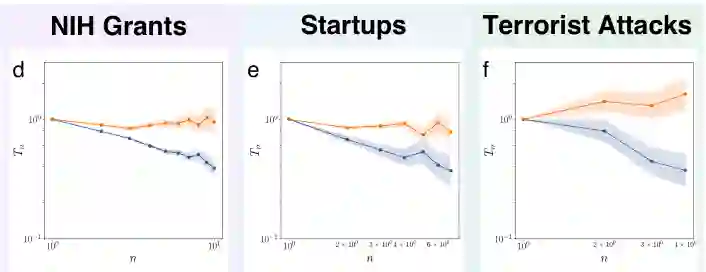
• 预测二 ：根据动力学信息所得到的早期信号，就足以将成功者和无法获得成功者分离开。

早期的信号就能将成功与失败分隔开，折线和阴影区域分别表示样本均值与方差

因为失败动力学作遵循的是幂律规律，即使是个体微观行为上的一点点差异也能在后期带来巨大的分流。这二者的分流其实在早期就以注定。

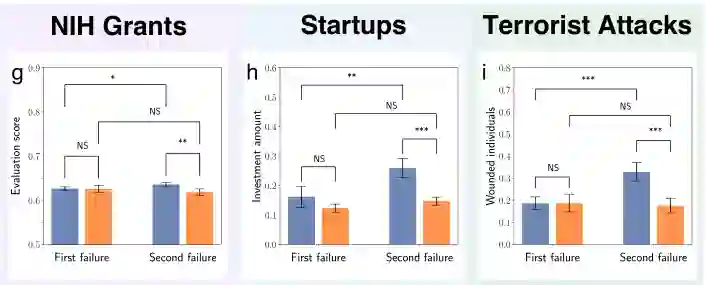
• 预测三： 实际能力的提升导致了分流的出现。

通过两次尝试的对比可以看到成功组和非成功组的学习能力差异巨大

通过观察上图我们可以发现，同样是经历失败，成功组和不成功组在经历失败后能力的提升并不相同。研究者通过这一思路也解决了，在观测三个来自真实数据库的数据时的疑问：为什么学习失败经验有用，但失败曲线的尾部却比较的“长”呢？研究者表示：成功与不成功的区别主要在于对待以往尝试中部件的复用上。

确实，学习以往经验、复用以前的部件能够保留足够优秀的资源，但也会使人们死死的攥住一个不太好的事物不肯放手，长时间的处于欠优的状态中。实际上，研究者在通过对真实数据的研究发现，那些事情进展停滞不前的人们并非倦于工作、懒于学习，而是做了太多不必要的事情。

而最终，研究者得出结论——

• 预测四： 失败曲线的长度服从韦伯分布（Weibull distribution）。

这就意味着，做一件事情在多次失败后，只要拟合了失败曲线的形状，我们就可以估计出该事件的未来的时间表：到底能否成功？何时会成功？

失之毫厘，谬以千里

以上这些结果表明，如果一次尝试的失败是构建在前期失败的基础之上，就能在早期阶段，通过重复失败的动力学信息刻画出相关的统计特征。传统上，人们会把胜败归功于运气、学习能力、和个体的差异。而本论文的研究者通过他们所构建的新模型给出了新的观点——

即使个体间的初始差异并不大，但在经过反复的学习过程后，所表现出来的结果却有着天壤之别。

正所谓：君子慎始，差若毫厘，谬以千里。

参考报道：

• How the data mining of failure could teach us the secrets of success

  https://www.technologyreview.com/s/613229/data-mining-reveals-the-hidden-secret-of-human-failure-and-how-to-turn-it-into-success/

本文转载自公众号“集智俱乐部”（ID:swarma_org）

---

更多故事，尽在👉领研网科研生涯频道。

▽ 精彩回顾 ▽