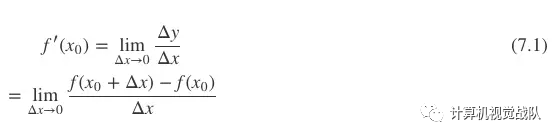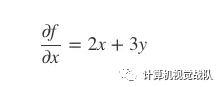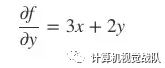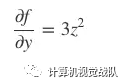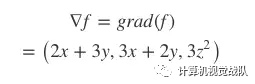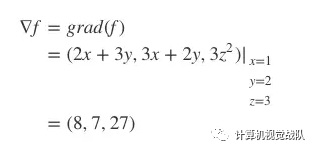简单易懂的讲解深度学习(入门系列之七)
简单易懂的讲解深度学习回顾:
1986年,辛顿教授和他的团队重新设计了BP算法,以“人工神经网络”模仿大脑工作机理,又一次将人工智能掀起了一个浪潮。但是,当风光不再时,辛顿和他的研究方向,逐渐被世人所淡忘,一下子就冷藏了30年。但在这30年里,辛顿有了新的想法。
于是在2006年,辛顿等人提出了“深度信念网(Deep Belief Nets,DBN)”(这实际上就是多层神经网络的前身)。这个“深度信念网”后期被称为“深度学习”。终于,辛顿再次闪耀于人工智能世界,随后被封为“深度学习教父”。
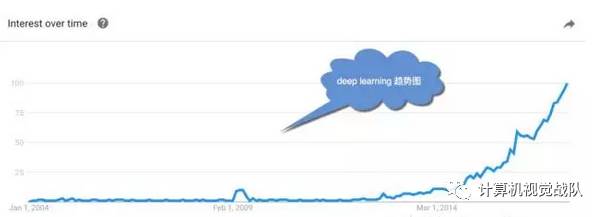
细心的您会发现,即使辛顿等人提出了“深度信念网”,在随后的小10年里,这个概念亦是不温不火地发展着(如图1所示)。直到2012年以后,随着大数据和大计算(GPU、云计算等)的兴起,深度学习才开始大行其道,一时间甚嚣尘上。
图7-1 深度学习的谷歌趋势图
回顾起杰弗里•辛顿过往40多年的学术生涯,可谓是顾跌宕起伏,但最终修得正果。
说起辛顿老师,我有幸和CV届大姐大,还有辛顿一起合影,很开心!O(∩_∩)O
图7-2 1986年杰弗里•辛顿的那篇神作
值得一提的是,在文献中,杰弗里•辛顿并不是第一作者,鲁梅尔哈特才是,而辛顿仅仅“屈居”第二(如图7-2所示)。但为什么我们提起BP算法时,总是说起辛顿呢?原因如下:
鲁梅尔哈特毕竟并非计算机科学领域之内的人士,我们计算机科学家,总不能找一个脑科学家去“拜码头”吧;
辛顿是这篇论文的通信作者,通常而言,通信作者才是论文思路的核心提供者,这样一来,即使作者排名第二,也没有埋没掉辛顿教授的贡献。
同在1986年,鲁梅尔哈特也和自己的小伙伴们合作发表了一篇题为“并行分布式处理:来自认知微结构的探索”的论文。仅仅从论文题目的前半部分来看,我们很可能误解这是一个有关“高性能计算”的文章,但从标题的后半部分可以得知,这是鲁梅尔哈特等人对人类大脑研究的最新认知。鲁梅尔哈特对大脑工作机理的深入观察,极大地启发了辛顿。辛顿灵光一现,觉得可以把这个想法迁移到“人工神经网络”当中。于是,就有了他们神来一笔的合作。
我们知道,1986年,辛顿和鲁梅尔哈特能在大名鼎鼎的《自然》期刊上发表论文,自然不是泛泛而谈,它一定是解决了什么大问题。
下面我们就聊聊这个话题。
多层感知机
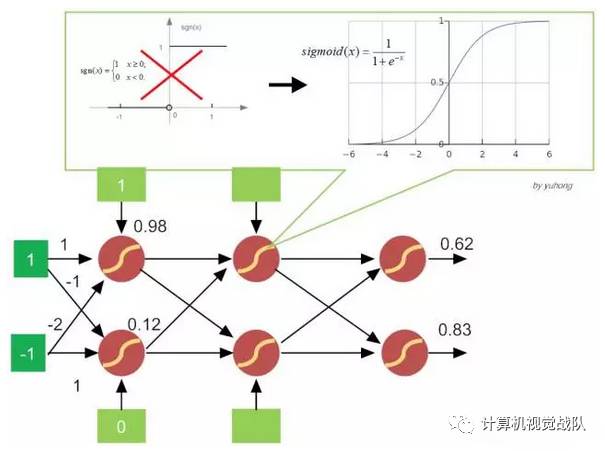
由于历史的惯性,在第六讲中提到的多层前馈网络,有时也被称为多层感知机(Multilayer Perceptron,MLP)。但这导致概念多少都有些混淆。这是因为,在多层前馈网络中,神经元的内部构造已发生变化,即激活函数从简单的“阶跃函数”变成了比较平滑的挤压函数Sigmoid(如图7-3所示)。
激活函数为什么要换成Sigmoid呢?其实原因并不复杂,这是因为感知机的激活函数是阶跃函数,不利于函数求导,进而求损失函数的极小值。我们知道,当分类对象是线性可分,且学习率(learning rate)η足够小时,感知机还不堪胜任,由其构建的网络,还可以训练达到收敛。但分类对象不是线性可分时,感知机就有点“黔驴技穷”了。因此,通常感知机并不能推广到一般前馈网络中。
图 7-3 变更激活函数的前馈多层神经网络
按照我们前面章节的说法,所谓的机器学习,简单来说,就是找到一个好用的函数(function),从而较好地实现某个特定的功能(function)。一言蔽之,函数就是功能。而对于某个特定的前馈神经网络,给定网络参数(连接权值与阈值),其实就是定义了一个具备数据采集(输入层)、加工处理(隐含层),然后输出结果(输出层)的函数。
如果仅仅给定一个网络结构,其实它定义的是一个函数集合。因为不同的网络参数(连接权值与阈值),实现的功能“大相径庭”。功能不同,自然函数也是不同的!
针对前馈神经网络,我们需要实现的目的很简单,就是想让损失函数达到最小值,因为只有这样,实际输出和预期输出的差值才最小。那么,如何从众多网络参数(神经元之间的链接权值和阈值)中选择最佳的参数呢?
最简单粗暴的方法,当然就是枚举所有可能值了!
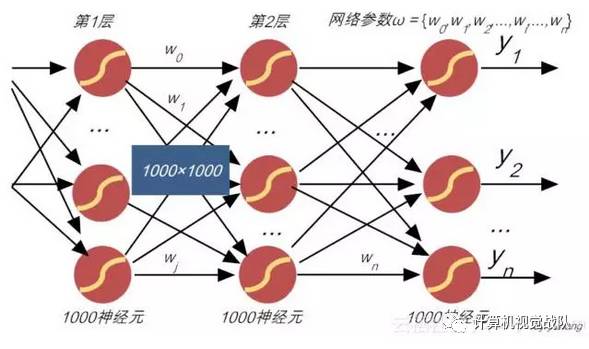
图7-4 暴力调参不可取
但这中暴力策略,对稍微复杂一点的网络就不可取了!例如,用于语音识别的神经网络,假设网络结构有7层,每一层有1000个神经元,那么仅一层之间的全连接权值,就达到10^6个,一旦层次多了,那权值数量就海了去了!(如图7-4所示)。故此,这种暴力调参找最优参数,既不优雅,也不高效,故实不可取!
到底什么是梯度
为了克服多层感知机存在的问题,人们设计了一种名为delta()法则(delta rule)的启发式方法,该方法可以让目标收敛到最佳解的近似值。
delta法则的核心思想在于,使用梯度下降(gradient descent)的方法找极值。具体说来,就是在假设空间中搜索可能的权值向量,并以“最佳”的姿态,来拟合训练集合中的样本。那么,何谓最佳拟合呢?当然就是让前文提到的损失函数达到最小值!
我们知道,求某个函数的极值,难免就要用到“导数”等概念。既然我们把这个系列文章定位为入门层次,那不妨就再讲细致一点。什么是导数呢?所谓导数,就是用来分析函数“变化率”的一种度量。针对函数中的某个特定点x0,该点的导数就是x0点的“瞬间斜率”,也即切线斜率,见公式(7.1)。
如果这个斜率越大,就表明其上升趋势越强劲。当这个斜率为0时,就达到了这个函数的“强弩之末”,即达到了极值点。而前文提到的损失函数,如果要达到损失最小,就难免用到导数“反向指导”如何快速抵达极小值。
在单变量的实值函数中,梯度就可以简单地理解为只是导数,或者说对于一个线性函数而言,梯度就是线的斜率。但对于多维变量的函数,它的梯度概念就不那么容易理解了。下面我们来谈谈这个概念。
在向量微积分中,标量场的梯度其实是一个向量场(vector filled)。对于特定函数的某个特定点,它的梯度就表示从该点出发,该函数值增长最为迅猛的方向(direction of greatest increase of a function)。假设一个标量函数f的梯度记为:f或grad这里的表示向量微分算子。那么,在一个三维直角坐标系,该函数的梯度就可以表示为公式(7.2):
求这个梯度值,难免要用到“偏导”的概念。说到“偏导”,这里顺便“轻拍”一下国内的翻译。“偏导”的英文本意是“partial derivatives(局部导数)”,书本上常翻译为“偏导”,可能会把读者的思路引导“偏”了。
derivatives(局部导数)”,书本上常翻译为“偏导”,可能会把读者的思路引导“偏”了。
那什么是“局部导数”呢?对于多维变量函数而言,当求某个变量的导数(相比于全部变量,这里只求一个变量,即为“局部”),就是把其它变量视为常量,然后整个函数求其导数。之后,这个过程对每个变量都“临幸”一遍,放在向量场中,就得到了这个函数的梯度了。举例来说,对于3变量函数:
f=x^2+3xy+y^2+z^3
它的梯度可以这样求得:
(1) 把 y, z视为常量,得 x的“局部导数”:
(2) 然后把 x, z视为常量,得 y的“局部导数”:
(3) 最后把 x, y视为常量,得 z的“局部导数”:
于是,函数 f的梯度可表示为:
针对某个特定点,如点A(1, 2, 3),带入对应的值即可得到该点的梯度:
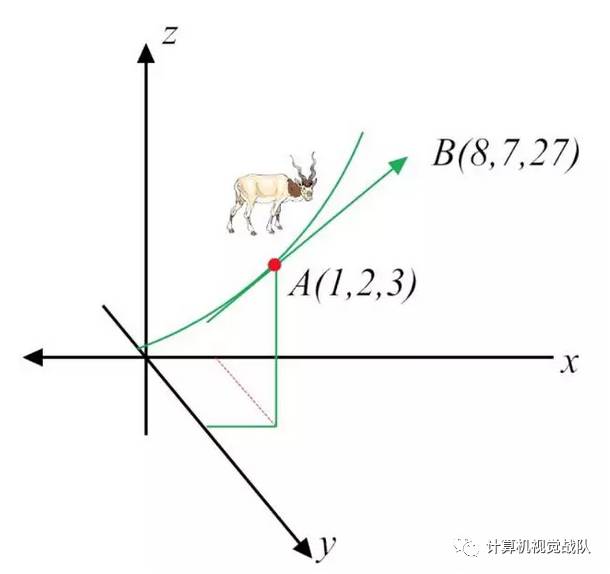
这时,梯度可理解为,站在向量点A(1, 2, 3),如果想让函数f的值增长得最快,那么它的下一个前进的方向,就是朝着向量点B(8,7,27)方向进发(如图7-3所示)。很显然,梯度最明显的应用,就是快速找到多维变量函数的极(大/小)值。
图7-5 梯度概念的示意图
在这里需要说明的是,我们用“局部导数”的翻译,仅仅是用来加深大家对“偏导”的理解,并不是想纠正大家已经约定俗成的叫法。所以为了简单起见,在后文我们还是将“局部导数”称呼为“偏导”。
到底什么是梯度下降
上面我们提到了梯度的概念,下面我们说说在求损失函数极小值过程中,常常提到的“梯度递减”的概念。
我们先给出一个形象的案例。爬过山的人,可能会有这样的体会,爬坡愈平缓(相当于斜率较小),抵达山峰(函数峰值)的过程就越缓慢,而如果不考虑爬山的重力阻力(对于计算机而言不存在这样的阻力),山坡越陡峭(相当于斜率越大),顺着这样的山坡爬山,就越能快速抵达山峰(对于函数而言,就是愈加快速收敛到极值点)。
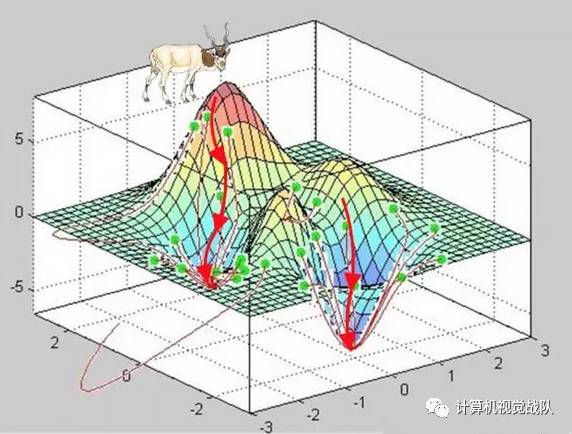
图7-6 梯度递减求极小值
如果我们把山峰“乾坤大挪移”,把爬山峰变成找谷底(即求极小值),这时找斜率最陡峭的坡而攀爬山峰的方法,并没有本质变化,不过是方向相反而已。如果把登山过程中求某点的斜率称为“梯度(gradient)”,而找谷底的方法,就可以把它称之为“梯度递减(gradient descent)”,示意图如图7-6所示。
依据“梯度递减”作为指导,走一步,算一步,一直遵循“最陡峭”的方向,探索着前进,这个过程,是不是有点像邓公的名句“摸着石头过河”?这个“梯度递减”体现出来的指导意义,就是“机器学习”中的“学习”内涵,即使在大名鼎鼎的“AlphaGo”中,“学习”这是这么玩的!你是不是有点失望?这机器学习也太不高大上了!
但别忘了,在第一讲中,我们就已经讲到“学习”的本质,在于性能的提升。利用“梯度递减”的方法,的确在很大程度上,提升了机器的性能,所以,它就是“学习”!
当然,从图7-3中,我们也很容易看到“梯度递减”的问题所在,那就是它很容易收敛到局部最小值。正如攀登高峰,我们会感叹“一山还比一山高”,探寻谷底时,我们也可能发现,“一谷还比一谷低”。但是“只缘身在此山中”,当前的眼界让我们像“蚂蚁寻路”一样,很难让我们有全局观,因为我们都没有“上帝视角”。
神经网络的损失函数
小结
在本章中,我们主要讲解了梯度的概念。所谓梯度,就是该函数值增长最为迅猛的方向,然后我们介绍了梯度下降法则。
在下一章中,我们将用最为通俗易懂的图文并茂的方式,给你详细解释反向传播(BP)算法<神经网络介绍—利用反向传播算法的模式学习>。BP算法不仅仅是作为经典,留在我们的记忆里,而且,它还“历久弥新”活在当下。要知道,深度信念网(也就是深度学习)之所以性能奇佳,不仅仅是因为它有一个“无监督”的逐层预训练(unsupervised layer-wise training),除此之外,预训练之后的“微调(fine-tuning)”,还是需要“有监督”的BP算法作为支撑。由此可见,BP算法影响之深,以至于“深度学习”都离不开它!
“世上没有白走的路,每一步都算数”。希望你能持续关注。
文章作者:张玉宏,著有《品味大数据》一书。