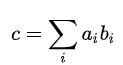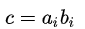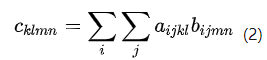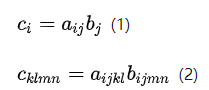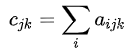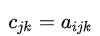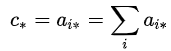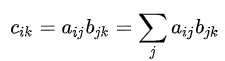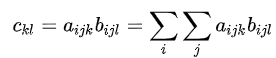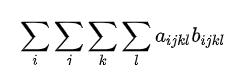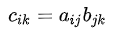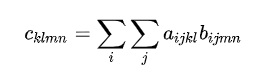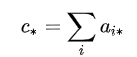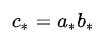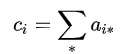einsum，一个函数走天下

会员服务 ·

einsum，一个函数走天下

2019 年 9 月 4 日 AI100

作者 | 永远在你身后

转载自知乎

【导读】einsum 全称 Einstein summation convention（爱因斯坦求和约定），又称为爱因斯坦标记法，是爱因斯坦 1916 年提出的一种标记约定，本文主要介绍了einsum 的应用。

简单的说，应用 einsum 就是省去求和式中的求和符号，例如下面的公式：

以 einsum 的写法就是：

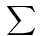
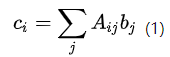
后者将符号给省去了，显得更加简洁；再比如：

上面两个栗子换成 einsum 的写法就变成：

在实现一些算法时，数学表达式已经求出来了，需要将之转换为代码实现，简单的一些还好，有时碰到例如矩阵转置、矩阵乘法、求迹、张量乘法、数组求和等等，若是以分别以 transopse、sum、trace、tensordot 等函数实现的话，不但复杂，还容易出错。

现在，这些问题你统统可以一个函数搞定，没错，就是 einsum，einsum 函数就是根据上面的标记法实现的一种函数，可以根据给定的表达式进行运算，可以替代但不限于以下函数：

矩阵求迹：trace
求矩阵对角线：diag
张量（沿轴）求和：sum
张量转置：transopose
矩阵乘法：dot
张量乘法：tensordot
向量内积：inner
外积：outer

该函数在 numpy、tensorflow、pytorch 上都有实现，用法基本一样，定义如下：

einsum(equation, *operands)

equation 是字符串的表达式，operands 是操作数，是一个元组参数，并不是只能有两个，所以只要是能够通过 einsum 标记法表示的乘法求和公式，都可以用一个 einsum 解决，下面以 numpy 举几个栗子：


  
  
    
   
   
     
    
    
      
    
    
      
   
   
     
   
   
     # 沿轴计算张量元素之和：c = a.sum(axis=0)

上面的以 sum 函数的实现代码，设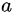为三维张量，上面代码用公式来表达的话就是：

换成 einsum 标记法：

然后根据此式使用 einsum 函数实现等价功能：


  
  
    
   
   
     
    
    
      
    
    
      
   
   
     
   
   
     c = np.einsum('ijk->jk', a)# 作用与 c = a.sum(axis=0) 一样

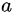
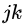
更进一步的，如果不止是三维，可以将下标换成省略号，以表示剩下的所有维度：

  
  
    
   
   
     
    
    
      
   
   
     
   
   
     c = np.einsum('i...->...', a)

这种写法 pytorch 与 tensorflow 同样支持，如果不是很理解的话，可以查看其对应的公式：

# 矩阵乘法c = np.dot(a, b)

矩阵乘法的公式为：

然后是 einsum 对应的实现：

  
  
    
   
   
     
    
    
      
   
   
     
   
   
     c = np.einsum('ij,jk->ik', a, b)

最后再举一个张量乘法栗子：


  
  
    
   
   
     
    
    
      
    
    
      
   
   
     
   
   
     # 张量乘法c = np.tensordot(a, b, ([0, 1], [0, 1]))

如果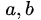是三维的，对应的公式为：

对应的 einsum 实现：

  
  
    
   
   
     
    
    
      
   
   
     
   
   
     c = np.einsum('ijk,ijl->kl', a, b)

下面以 numpy 做一下测试，对比 einsum 与各种函数的速度，这里使用 python 内建的 timeit 模块进行时间测试，先测试（四维）两张量相乘然后求所有元素之和，对应的公式为：

然后是测试代码：


  
  
    
   
   
     
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
   
   
     
   
   
     from timeit import Timerimport numpy as np
# 定义两个全局变量a = np.random.rand(64, 128, 128, 64)b = np.random.rand(64, 128, 128, 64)
# 定义使用einsum与sum的函数def einsum():    temp = np.einsum('ijkl,ijkl->', a, b)    def npsum():    temp = (a * b).sum()
# 打印运行时间print("einsum cost:", Timer("einsum()", "from __main__ import einsum").timeit(20))print("npsum cost:", Timer("npsum()", "from __main__ import npsum").timeit(20))

上面 Timer 是 timeit 模块内的一个类

Timer(stmt, setup).timeit(number)    # stmt: 要测试的语句    # setup: 传入stmt的运行环境，比如stmt中要导入的模块等。    # 可以写一行语句，也可以写多行语句，写多行语句时要用分号；隔开语句    # number: 执行次数

将两个函数各执行 20 遍，最后的结果为，单位为秒：

einsum cost: 1.5560735npsum cost: 8.0874927

可以看到，einsum 比 sum 快了几乎一个量级，接下来测试单个张量求和：

将上面的代码改一下：


  
  
    
   
   
     
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
   
   
     
   
   
     def einsum():    temp = np.einsum('ijkl->', a)    def npsum():    temp = a.sum()

相应的运行时间为：

einsum cost: 3.2716003npsum cost: 6.7865246

还是 einsum 更快，所以哪怕是单个张量求和，numpy 上也可以用 einsum 替代，同样，求均值（mean）、方差（var）、标准差（std）也是一样。

接下来测试 einsum 与 dot 函数，首先列一下矩阵乘法的公式以以及 einsum表达式：

然后是测试代码：


  
  
    
   
   
     
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
   
   
     
   
   
     a = np.random.rand(2024, 2024)b = np.random.rand(2024, 2024)
# einsum与dot比较def einsum():    res = np.einsum('ik,kj->ij', a, b)
def dot():    res = np.dot(a, b)
print("einsum cost:", Timer("einsum()", "from __main__ import einsum").timeit(20))print("dot cost:", Timer("dot()", "from __main__ import dot").timeit(20))
# einsum cost: 80.2403851# dot cost: 2.0842243

这就很尴尬了，比 dot 慢了 40 倍（并且差距随着矩阵规模的平方增加），这还怎么打天下？不过在 numpy 的实现里，einsum 是可以进行优化的，去掉不必要的中间结果，减少不必要的转置、变形等等，可以提升很大的性能，将 einsum 的实现改一下：


  
  
    
   
   
     
    
    
      
    
    
      
   
   
     
   
   
     def einsum():    res = np.einsum('ik,kj->ij', a, b, optimize=True)

加了一个参数 optimize=True，官方文档上该参数是可选参数，接受4个值：

optimize : {False, True, ‘greedy’, ‘optimal’}, optional

optimize 默认为 False，如果设为 True，这默认选择‘greedy（贪心）’方式，再看看速度：

einsum cost: 2.0330937dot cost: 1.9866218

可以看到，通过优化，虽然还是稍慢一些，但是 einsum 的速度与 dot 达到了一个量级；不过 numpy 官方手册上有个 einsum_path，说是可以进一步提升速度，但是我在自己电脑上（i7-9750H）测试效果并不稳定，这里简单的介绍一下该函数的用法为：


  
  
    
   
   
     
    
    
      
    
    
      
   
   
     
   
   
     path = np.einsum_path('ik,kj->ij', a, b)[0]np.einsum('ik,kj->ij', a, b, optimize=path)

einsum_path 返回一个 einsum 可使用的优化路径列表，一般使用第一个优化路径；另外，optimize 及 einsum_path 函数只有 numpy 实现了， tensorflow 和 pytorch 上至少现在没有。

最后，再测试 einsum 与另一个常用的函数 tensordot，首先定义两个四维张量的及 tensordot 函数：


  
  
    
   
   
     
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
   
   
     
   
   
     a = np.random.rand(128, 128, 64, 64)b = np.random.rand(128, 128, 64, 64)
def tensordot():    res = np.tensordot(a, b, ([0, 1], [0, 1]))

该实现对应的公式为：

所以 einsum 函数的实现为：


  
  
    
   
   
     
    
    
      
    
    
      
   
   
     
   
   
     def einsum():    res = np.einsum('ijkl,ijmn->klmn', a, b, optimize=True)

tensordot 也是链接到 BLAS 实现的函数，所以不加 optimize 肯定比不了，最后结果为：


  
  
    
   
   
     
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
   
   
     
   
   
     print("einsum cost:", Timer("einsum()", "from __main__ import einsum").timeit(1))print("tensordot cost:", Timer("tensordot()", "from __main__ import tensordot").timeit(1))
# einsum cost: 4.2361331# tensordot cost: 4.2580409

测试了 10 多次，基本上速度一样，einsum 表现好一点的；不过说是一个函数打天下，肯定是做不到的，还有一些数组的分割、合并、指数、对数等功能没法实现，需要使用别的函数，其他的基本都可以用 einsum 来实现，简单而又高效。

经过进一步测试发现，优化反而出现速度降低的情况，例如：


  
  
    
   
   
     
    
    
      
    
    
      
    
    
      
    
    
      
    
    
      
   
   
     
   
   
     def einsum():    temp = einsum('...->', a, optimize=True)
def test():    temp = a.sum()

上面两中对数组求和的方法，当a是一维向量时，或者 a 是多维但是规模很小是，优化的 einsum 反而更慢，但是去掉 optimize 参数后表现比内置的 sum函数稍好，我认为优化是有一个固定的成本。

还有一个坑需要注意的是，有些情况的省略号不加 optimize 会报错，就拿上面的栗子而言：


  
  
    
   
   
     
    
    
      
    
    
      
   
   
     
   
   
     np.einsum('...->', a, optimize=True)   # 正常运行np.einsum('...->', a)   # 报错

很无奈，试了很多次，不加 optimize 就是会报错，但是并不是所有的省略号写法都需要加 optimize ，例如：

使用省略号实现上面两个公式并不需要加 optimize ，能够正常运行


  
  
    
   
   
     
    
    
      
    
    
      
   
   
     
   
   
     np.einsum('i...->...', a)   # 正常np.einsum('...,...->...', a, b)   # 正常

但是如果碰到下面的公式：

上式表示将 a 除第一个维度之外，剩下的维度全部累加，这种实现就必须要加 optimize。

  
  
    
   
   
     
    
    
      
   
   
     
   
   
     np.einsum('i...->i', a, optimize=True)   # 必须加optimize，不然报错

再举一个栗子：


  
  
    
   
   
     
    
    
      
    
    
      
    
    
      
   
   
     
   
   
     c = (a * b).sum()# 如果不知道a, b的维数，使用einsum实现上面的功能也必须要加optimizec = einsum('...,...->', a, b, optimize=True)