这些东西，看过的人都转疯了！

不知道大家的朋友圈里是不是天天有什么

「转疯了，这些东西居然都不能吃！」

「你赚得再多有什么用，这篇文章在朋友圈转疯了」

「大家都在转！这周末居然有这么劲爆的事」

今天，小编就带大家看看

那些真的「转疯了」的东西

是啥样的

转转小玩具

Physics Toys

▲ 现在市面上这类玩具越来越多，这种转而不倒的现象确实很神奇，这种现象在物理上被称为进动。重力其实在这里起到的作用不是使其倒下而是让其转起来，如果里面的陀螺不转的话是没有这种效果的哦

▲ 高速旋转的陀螺不会倒下的原理正是上面提到的内容。上图中陀螺底部沿着蚊香状图案的边缘移动，不会被甩出去

▲ 在一杯水上我们放上如上装置，点燃蜡烛以后位于铜管内的气体受热膨胀，提供力矩从而推动小船旋转，因为水面上阻力并不大，旋转的量看起来还是很可观的

▲ 魔方，也叫鲁比克方块，最早是由匈牙利布达佩斯建筑学院厄尔诺·鲁比克教授于1974年发明的。其最基本的操作就是通过旋转来还原其每一个面。利用部分旋转的不可交换性，也就是先转 A 面再转 B 面和先转 B 面和 A 面对魔方形状的影响并不同，我们可以自创一些麻烦但是很有效的魔方解法，比如先转 A 再转 B 再倒着转 A 再倒着转 B，仅有部分魔方上的块会受到影响，一些基础的魔方教程上的转动公式都是这么来的。赶紧拿起手中的魔方试一试吧~

▲ 这是一个乒乓球，不过在其表面上我们将其钻了两个洞。放入液氮之中再取出，此时因为乒乓球里面流入了液氮，所以会剧烈地沸腾往外喷射气体，带动乒乓球高速旋转

脑补一下~

Let's Imagine~

▲ 不知道大家能不能脑补出来一个在旋转的圆环。

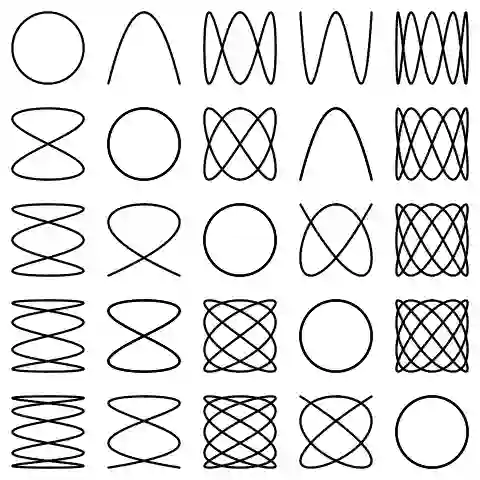
▲ 利萨如（Lissajous）曲线两个沿着互相垂直方向的简谐振动的合成的轨迹，上图在运动是因为两者之间的相位差在不断变化。经常操作示波器的想必对这些图案再熟悉不过。如果我们把其中一个方向的简谐运动想象成一个绕着圆心旋转的一个圆周上质点的投影，那么利萨如图形就可以想象成一个在 3 维的圆柱上面画有正弦图案并且不断转动了~

▲ 不过我们这种脑补能力显然还不够去想象 4D 的物体是怎么运动的，虽然我们已经看到了它的投影在我们的三维空间是怎么运动的……

三体问题

Three Body Problem

说到旋转，我们就不得不提到三体。两个物体在万有引力的作用下互相绕着其共同质心旋转，但是三个物体呢？

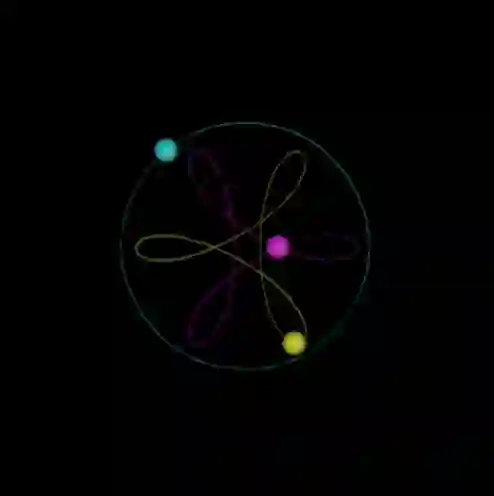
▲ 以为大刘写的科幻小说《三体》的大火，现在提到三体问题基本上大家都能说上来这是啥。它是指三个质量、初始位置和初始速度都是任意的可视为质点的天体，在相互之间万有引力的作用下的运动规律问题。现在已知，三体问题不能精确求解，即无法预测所有三体问题的数学情景

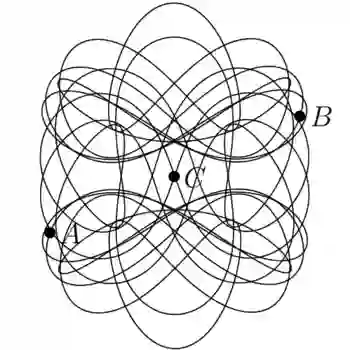
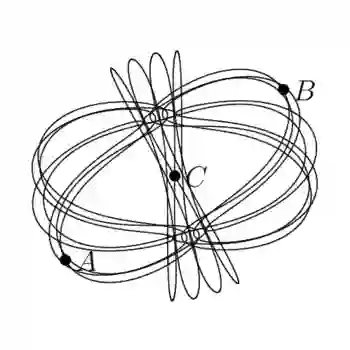
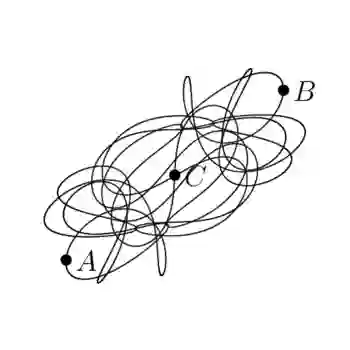
▲ 一些更加复杂的三体运动轨道

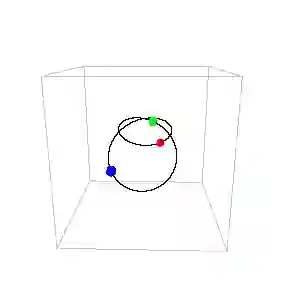
▲ 三体问题实际上并没有限制在平面内运动

来一首天鹅湖~

Лебединое озеро

▲ 上面这个实验往往被用来向大家展示角动量守恒，双臂伸出时，转动惯量较大，转动的角速度比较小，但是当双臂收紧，转动惯量较小，相应的转动角速度就比较大

▲ 当然，我们也可以用另外的实验来展示转动惯量对物体转动速度的影响，在提供相同外部力矩的情况下，转动惯量小的转动地更快

▲ 在芭蕾舞蹈中，就用到了这一物理原理

▲ 舞者通过改变自己的体态，可以调节自身转动惯量的大小，从而展现多变而又优美的舞姿

▲ 通过收紧大腿，改动自己的手所在的位置，就可以自由地控制旋转的快慢

齿轮表示别忘了我

Gear

▲ 用于将倒着转和正着转都转换成同一个旋转方向的齿轮

▲ 将往复运动转化为旋转的齿轮

▲ 现在市面上这类玩具越来越多，这种转而不倒的现象确实很神奇，这种现象在物理上被称为进动。重力其实在这里起到的作用不是使其倒下正是让其转起来，如果里面的陀螺不转的话是没有这种效果的哦

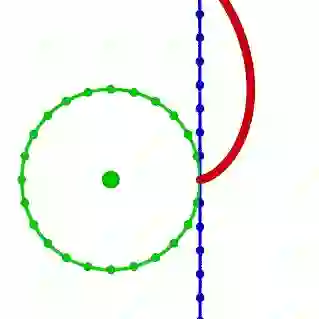
▲ 所谓摆线如图所示，就是直线在圆周上做无滑动滚动，直线上某点的轨迹

▲ 另一种摆线

网球拍定理

Tennis Racket Theorem

将网球拍抛向空中，你看看它们会绕着哪根轴旋转？如果没有网球拍的话，往空中扔一个手机也可以，不舍得把手机砸了可以扔一本书啥的

这些转动一般只会沿着特定的某个轴，而不是想象中的三个方向旋转都有可能。

▲ 该现象由俄罗斯宇航员弗拉基米尔·扎尼别科夫于1985年在太空中发现, 也被称为网球拍定理或者中间轴定理. 在物体转动时, 绕其主轴的转动是不稳定的.

最后给大家送张「好看」的图

The Belt Trick

▲ 仔细观察，这个系统要转多少度才能回到自身呢？

参考链接：

封面图来自 unsplash，文中动图来自 Giphy 以及 reddit.com/r/gif，文内扩展内容阅读请点击以下标题

[1] rotational inertia demo

[2] 芭蕾舞蹈与天鹅湖 - TED

[3] 为什么手机只能围绕三个对称轴其中的两个稳定地旋转？

编辑：Cloudiiink

---

---

近期热门文章Top10

↓ 点击标题即可查看 ↓

1. 女生冬天穿那么少不冷吗？我找了个男生试了下......

2. 严肃科普：如何区分奥特曼

3. 人类花百年规划设计的铁路网，这些无脑生物26小时就搞定了

4. 2018 年最冷科学知识 Top 10

5. 一幅图读懂量子力学（Ⅳ）

6. Physics World 评选出2018年度十大科学突破

7. 昨晚，我在秋名山输给了一个沙发……

8. 假如有人告诉你这个世界的本质是弹簧，你愿意相信吗？

9. 磁铁可以只有一极吗？它或许能打开万物理论之门

10. 上坡要刹车; 下坡踩油门，关于怪坡你了解多少？

点此查看以往全部热门文章

---