三、CRF概率计算问题

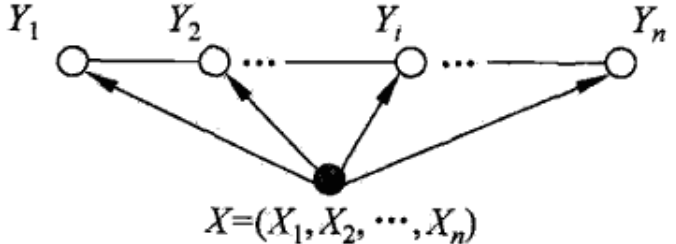
给定模型参数、输入序列{x1,x2,…,xn}和输出序列{y1,y2,…,yn}的前提下，计算条件概率p(y|x)。

由定义可知

$$ P\left( y|x \right) = \frac{1}{Z}e^{\sum_{}{}{\lambda f(x,yc)}} $$

$$ Z = \sum_{Y}^{}e^{\sum_{}{}{\lambda f(x,yc)}} $$

但是实际计算的时候，我们会发现Z的计算非常复杂，需要很多时间。这里我们介绍一种多项式时间的特殊算法——前向-后向算法。这是一种动态规划算法，和Viterbi算法很像，适用于一种特殊的CRF——线性链条件随机场。

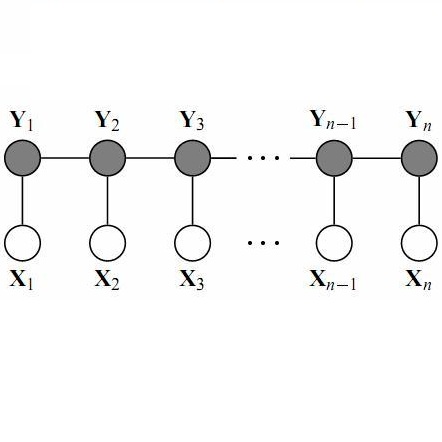
线性链条件随机场： 设X={X1,X2,……,Xn}，Y={Y1,Y2,……,Yn}均为线性链表示的随机变量序列，若在给定随机变量序列X的前提下，随机变量Y的条件概率分布P(Y|X)是马尔科夫随机场，即

$P(Y_i|X, Y_1,...,Y_{i-1},Y_(i+1),...,Y_n)=P({Y_i}|X,Y_{i-1},Y_{i+1})$ 则称P(Y|X)为线性链条件随机场

图模型如下：

这种条件随机场在文本处理，编码解码，时序状态相关模型等领域得到了广泛使用，值得专门拿出来提一下。

显然，这种条件随机场的最大团为${Y_1,Y_2}$,${Y_2,Y_3}$,…, ${Y_{n-1},Yn}$，于是我们可以得到

$$ P\left( y|x \right) = \frac{1}{Z}exp(\sum_{}{}{\lambda f(x,y_{t - 1},y_{t})}) $$

$$ Z = \sum_{Y}{}{exp(\sum_{}{}{\lambda f(x,y_{t - 1},y_{t})})} $$

如果所有的λ都已知，计算后面的$exp(\sum_{}{}{\lambda f(x,y_{t - 1},y_{t})})$非常轻松，但是想计算Z就非常麻烦了，打个比方，每个$y_{t}$都有m=10种取值，序列长度为n=10，那么所有可能的y就有$10{10}$种，计算量实在太大。

不过我们可以注意到，这个序列最大团的大小都是2，满足无后效性，所以可以采用动态规划法求解——也就是前向-后向算法。

前向-后向算法

下面开始正式介绍前向-后向算法。

定义：

前向向量αi(x)：

$$\alpha_0(x|y)= { \{_{0,y = start}^{1,y = others} } $$

递推公式为：

$$ \alpha_{i}{T}(x) = \alpha_{i - 1}{T}(x)M_{i}(x) $$

这里的$M_{i}(x)$来自之前的条件随机场的矩阵形式。

$\alpha_{i}(y|x)$的含义是从1到位置i，且位置i为y的序列的概率（没有归一化），由于y有m种取值，显然$\alpha_{i}{T}(x)$是一个m维向量

后向向量βi(x):

$$ \beta_{n+1}(y|x)={\{_{1,y=stop}^{0,y=others}} $$

递推公式为：

$$ \beta_{i}(x) = M_{i + 1}(x)\beta_{i + 1}(x) $$

$\beta_{i}(y|x)$的含义是从位置i到n，且位置i为y的序列的概率（没有归一化），显然$\beta_{i}(x)$也是m维向量。

由上面这两个定义，我们知道归一化概率为

$$ Z\left( x \right) = \alpha_{n}^{T}\left( x \right) 1 = 1^{T} \beta_{1}\left( x \right) $$

在给定X=x的前提下，序列Y的第i个位置为yi的条件概率为

$$ P\left( Y_{i} = y_{i} | x \right) = \frac{\alpha_{i}{T}(y_{i}|x)\beta_{i}(y_{i}|x)}{Z(x)} $$

第i-1个位置为$y_{i - 1}$，同时第i个位置为$y_{i}$的条件概率为

$$P(Y_{i-1}=y_{i-1},Y_i = y_i |x)=\frac{{{\alpha_i}^T}(y_{i-1}|x){M_i}(y_{i-1},y_i|x){{\beta_i}(y_i|x)}}{Z(x)}$$

由此我们很容易得到序列y关于x的条件概率

$$ P\left( y | x \right) = P\left( Y_{1} = y_{1} | x \right)\prod_{i = 2}^{n}{P\left( Y_{i - 1} = y_{i - 1},Y_{i} = y_{i} | x \right)} $$

这个问题就解决了，bingo。

别慌，利用前向后向向量，我们可以得到两个很重要的东西

特征函数 $\mathbf{f}_{\mathbf{k}}$ 关于条件概率分布P(Y|X)的期望 ：

$E_{P(Y|X)}(f_k)=\sum_{y}P(y|x){f_k}(y,x)$

$={\sum_{i=1}^{n+1}}y_{i-1} \sum y_i f_k(y_{i-1},y_i,x,i)\bullet{\frac{{\alpha_i}^T(y_{i-1}|x)M_i (y_{i-1},{y_i}|x){\beta_i}(y_i|x)}{Z(x)}}$

以及特征函数$\mathbf{f}_{\mathbf{k}}$关于联合概率分布P(X,Y)的期望：

$$ E_{P(X,Y)}(f_{k}) = \sum_{x,y}{}{P(x,y)\sum_{i = 1}^{n + 1}{f_{k}(y_{i - 1},y_{i},x,i)}} $$

其中$P(x,y)$可以使用数据分布$\tilde{P}(X)$进行估计

$$ P\left( x,y \right) = \tilde{P}\left( x \right) P(y|x) $$

这两个东西看起来又复杂又没用，但却是梯度下降法中的关键一步。

根据这个算法，我们只需要一次前向扫描得到α，一次后向扫描得到β，即可得到所有特征函数的期望以及条件概率分布。

Reference：

《统计学习方法》李航

https://www.zhihu.com/question/20380549/answer/45066785 宁远成梁

https://zhuanlan.zhihu.com/p/26696451