四、CRF学习问题

这一篇是使用CRF的核心。

还是那句话，不能求解的模型没有任何意义，CRF的优点在于，它在较好地模拟现实的同时，能够比较轻松地进行学习，而且还是凸优化问题，可以直接使用万能的梯度下降法求解。

CRF的求解方法有很多种，这里我只介绍一下梯度下降算法。

梯度下降法

身为概率图模型，自然有迭代算法EM可以适用，嫌弃计算量大收敛慢的话还可以试试Gibbs采样。

不过说起最通用最广泛的算法还是梯度下降法，作为一个凸优化模型，可以很轻松地与其他凸优化模型融合，从而得到更广泛的应用。可以说，学会了这一个算法，其他的会不会都无所谓

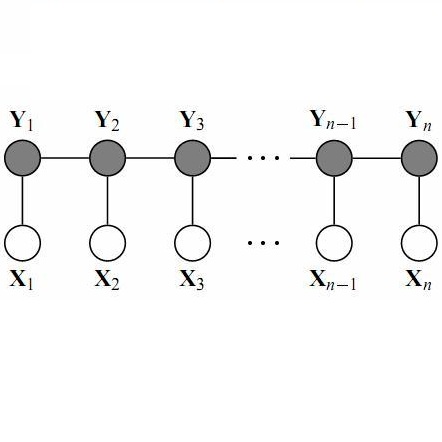
这里同样采用线性链条件随机场作为例子。

线性链CRF，给定x 求某一y序列的概率为：

$$ P\left( y|x \right) = \frac{1}{Z}\prod_{t = 1}^{T}{\exp\left( \sum_{k = 1}^{K}{\lambda_{k}f_{k}\left( x,y_{t - 1},y_{t} \right)} \right)}(1) $$

其中分母Z(x)是归一因子： $$ Z\left( x \right) = \sum_{y}^{}{\prod_{t = 1}^{T}{\exp\left( \sum_{k = 1}^{K}{\lambda_{k}f_{k}\left( x,y_{t - 1},y_{t} \right)} \right)}}(2) $$ 它在较好地模拟现实的同时，能够比较轻松地求解

公式(2) 中的y就是所有可能的序列，计算开销很大。

给出似然函数的对数表达式：

$$ \ln\left( L\left( \theta \right) \right) = \sum_{i = 1}^{N}{(\sum_{t = 1}^{T}{\sum_{k = 1}^{K}{\lambda_{k}f_{k}\left( x,y_{t - 1},y_{t} \right) -}}ln(Z(x)))} (3) $$

其中N是训练序列的个数，现在我们要用随机梯度下降法（SGD）来极大似然函数（准确地说应该是梯度上升法），因此每次只用处理一个训练序列，于是有：

$$ \ln\left( p(y|x) \right) = \sum_{t = 1}^{T}{\sum_{k = 1}^{K}{\lambda_{k}f_{k}\left( x,y_{t - 1},y_{t} \right) -}}\ln\left( Z\left( x \right) \right)(4) $$

参数更新：

$$ \lambda_{k} = \lambda_{k} + \alpha \frac{{\partial ln}\left( p(y|x) \right)}{\partial\lambda_{k}}(5) $$

到这里，大家可以停一下，先试着自己求一下梯度，如果遇到困难了再接着往下看。

对第k个特征函数求偏导，得到：

$$ \frac{{\partial ln}\left( p(y|x) \right)}{\partial\lambda_{k}} = \sum_{t = 1}^{T}{f_{k}\left( x,y_{t - 1},y_{t} \right)} - \frac{1}{Z\left( x \right)}\frac{\partial Z\left( x \right)}{\partial\lambda_{k}} (6) $$

第一项非常简单，现在我们来对第二项进行求解。

$$ \frac{1}{Z\left( x \right)}\frac{\partial Z\left( x \right)}{\partial\lambda_{k}} = \frac{1}{Z\left( x \right)}\sum_{y}{}{\left( \exp{\left( \sum_{t = 1}^{T}{\sum_{k = 1}^{K}{\lambda_{k}f_{k}\left( x,y_{t - 1},y_{t} \right)}} \right) \sum_{t = 1}^{T}{f_{k}\left( x,y_{t - 1},y_{t} \right)}} \right)(7)} $$

注意到 $$ P\left( y|x \right) = \frac{1}{Z}\exp\left( \sum_{t = 1}^{T}{\sum_{k = 1}^{K}{\lambda_{k}f_{k}\left( x,y_{t - 1},y_{t} \right)}} \right) $$ 而 Z(x)对于一个训练序列来讲是常数，所以可以拿到括号里面，化简得到：

$$ \frac{1}{Z\left( x \right)}\frac{\partial Z\left( x \right)}{\partial\lambda_{k}} = \sum_{y}{}{\left( {p(y|x)}{\sum_{t = 1}^{T}{f_{k}\left( x,y_{t - 1},y_{t} \right)}} \right)(8)} $$

这一步很漂亮，接着：

$$ \frac{{\partial ln}\left( p(y|x) \right)}{\partial\lambda_{k}} = \sum_{t = 1}^{T}{f_{k}\left( x,y_{t - 1},y_{t} \right)} - \sum_{y}^{}{\left( {p(y|x)}{\sum_{t = 1}^{T}{f_{k}\left( x,y_{t - 1},y_{t} \right)}} \right)(9)} $$

推导完毕，这个式第一项是真实值，第二项是期望值，当两者相等时，梯度为0，迭代停止。

而之前在介绍前向-后向算法的时候，已经指出特征函数的期望可以用

$$E_{P(Y|X)}(f_k)=\sum_{y}P(y|x){f_k}(y,x)={\sum_{i=1}^{n+1}} \sum_{y_{I-1},y_i} f_k(y_{i-1},y_i,x,i)\bullet{\frac{{\alpha_i}^T(y_{i-1}|x)M_i (y_{i-1},{y_i}|x){\beta_i}(y_i|x)}{Z(x)}}$$

来求解，于是这个问题就解决了。

Reference：

《统计学习方法》李航

https://www.zhihu.com/question/20380549/answer/45066785 宁远成梁 https://zhuanlan.zhihu.com/p/26696451