条件随机场 (CRF 入门)——应用举例- 专知

会员服务 ·

条件随机场 (CRF 入门)——应用举例

ZGH

六、CRF应用举例

CRF应用广泛，常用于句法分析、命名实体识别、词性标注等。

CRF有许多工具包，代表有crf++, crfsuite, crfsgd, wapiti等，不过大部分都已经好久不更新了，与其学习工具的使用，倒不如自己写。

下面还是以第一篇文章中的例子来阐述如何实现CRF。

回顾：小明一日三餐吃什么和他的位置有关，假如学校有123三个校区，相邻两餐的间隔时间只够他从一个校区转移到相邻的校区，而每个校区食堂的饭菜有相同也有不同。

输入：一组训练数据，包含小明三餐的食物和用餐的地点

输出：一个CRF模型，可以通过小明三餐的食物对用餐地点进行预测

建模：

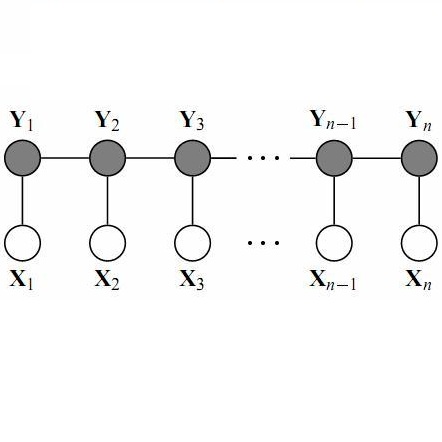
三餐所吃的食物为随机变量X={x1,x2,x2}，对应的用餐地点为随机变量Y={y1,y2,y3}。根据题意可以得到如下模型，每个时间所处地点仅仅与前一个时间有关

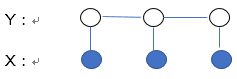
在X已知的条件下，Y构成马尔科夫随机场，图中一共有两个最大团{y1,y2}和{y2,y3}，于是一共有两类特征函数F(y1,y2,x)与F(y2,y3,x)

根据之前的CRF简化形式，我们有：

$$ P\left( y|x \right) = \frac{1}{Z}\exp\left( \sum_{k1 = 1}^{K1}{\lambda_{k1}f_{k1}\left( x,y_{1},y_{2} \right)} + \sum_{k2 = 1}^{K2}{\lambda_{k2}f_{k2}\left( x,y_{2},y_{3} \right)} \right) $$

显然，对于每个训练样本，我们的目标是将输入x输出y对应的概率$P\left( y|x \right)$最大化，整体的似然函数为

$$ \ln\left( L\left( \theta \right) \right) = \sum_{i = 1}^{N}{(\sum_{k1 = 1}^{K1}{\lambda_{k1}f_{k1}\left( x,y_{1},y_{2} \right)} + \sum_{k2 = 1}^{K2}{\lambda_{k2}f_{k2}\left( x,y_{2},y_{3} \right)}) - \ln(Z(x)))} $$

为了简单起见，这里我们用随机梯度下降算法，每次只输入一个样本

$$ \ln\left( p(y|x) \right) = \sum_{k1 = 1}^{K1}{\lambda_{k1}f_{k1}\left( x,y_{1},y_{2} \right)} + \sum_{k2 = 1}^{K2}{\lambda_{k2}f_{k2}\left( x,y_{2},y_{3} \right)} - \ln\left( Z\left( x \right) \right) $$

参数更新

$$ \lambda_{k} = \lambda_{k} + \alpha\frac{\partial ln\left( p(y|x) \right)}{\partial\lambda_{k}} $$

其中$$Z\left( x \right) = \sum_{y}^{}{\exp\left( \sum_{k1 = 1}^{K1}{\lambda_{k1}f_{k1}\left( x,y_{1},y_{2} \right)} + \sum_{k2 = 1}^{K2}{\lambda_{k2}f_{k2}\left( x,y_{2},y_{3} \right)} \right)}$$

由之前的推导我们知道

$$ \frac{\partial ln\left( p(y|x) \right)}{\partial\lambda_{k}} = f_{k}\left( x,y_{t - 1},y_{t} \right) - E_{P\left( Y|X \right)}\left( f_{k} \right) $$

再由前向后向算法算出第二项

$$E_{P(Y|X)}(f_k)=\sum_{i=1}^{n+1}\sum_{y_{i-1},y_i}f_k(x,y_{i-1},y_i)\bullet\frac{{\alpha_i}^T (y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)}$$

于是我们得到了如下完整的算法流程：

输入：所有训练数据X，Y

输出：参数λ

（1）初始化：

随机初始化参数λ

（2）循环开始：

随机挑选一个输入x,y

使用前向后向算法，计算此时参数λ下所有特征函数的期望$E_{P\left( Y|X \right)}\left( f_{k} \right)$

使用随机梯度下降算法对所有的参数进行更新

$$ \lambda_{k} = \lambda_{k} + \alpha(f_{k}\left( x,y_{t - 1},y_{t} \right) - E_{P\left( Y|X \right)}\left( f_{k} \right)) $$