二、CRF数学定义

这篇文章里，我会从条件随机场的概念出发，详细阐述CRF的定义以及常用的各种形式的由来，不过若是赶时间的话，直接拉到文章末尾看一下CRF简化形式基本就够了。

条件随机场： 给定一组输入随机变量X的条件下，另一组输出随机变量Y的条件概率分布模型，若输出随机变量Y是一个由图G=(V,E)表示的马尔科夫随机场，即

$$ P\left( Y_{v}|X,Y_{w},w \neq v \right) = P\left( Y_{v}|X,Y_{w},w \sim v \right) $$

对任意结点v成立，则称条件概率分布P(Y|X)为条件随机场，式中w≠v表示除v之外的所有结点，w~v表示与v相连的所有结点。

公式虽然非常简明准确，但看起来未免有些令人头痛，用通俗易懂的语言解释就是——1）计算某个点的条件概率，只用计算与之相关的随机变量为条件。2）该条件概率分布具有马尔可夫性

第一点应该非常好懂，这也是条件随机场和马尔科夫随机场最大的区别所在：每个点在其他点的条件下的条件概率具有马尔可夫性，而不是联合概率分布具有马尔科夫性。

第二点属于第一点的补充，虽然和第一点是一个概念的两种说法，但蕴含了定义中没有直接提出的，一个概率图模型中最重要的定理——Hammersley Clifford定理！

Hammersley Clifford定理：概率无向图模型（即马尔科夫随机场）的联合概率分布P(Y)可以表示成如下形式：

$$ P\left( Y \right) = \frac{1}{Z}\prod_{C}{}{\Psi_{c}(Y_{c})} $$

$$ Z = \sum_{Y}{}{\prod_{C}{}{\Psi_{c}(Y_{c})}} $$

其中C是无向图中的最大团，$Y_{c}$是C的结点对应的随机变量，$\Psi_{c}\left( Y_{c} \right)$是C上定义的严格正函数，乘积是在无向图上所有最大团上进行。

简单来说就是马尔科夫随机场可以因式分解，而因式分解可以大大地降低计算的复杂度。

那么可以因式分解成哪几个部分呢？

答：最大团

最大团定义：无向图G中任意两个结点均有边连接的结点子集称为团（clique）。

若C是无向图G中的一个团，且不能加入G中任意结点使其成为一个更大的团，则称C为无向图G的一个最大团。

团的定义好理解，举几个例子就懂了。

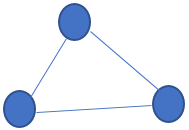
两个结点的团：

三个结点的团：

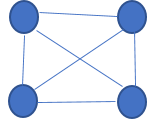
四个结点的团：

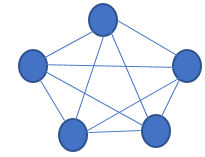
五个结点的团：

其实团就是完全图，每次想加一个结点形成一个更大的团，就需要这个结点与之前所有已有的结点都有边相连，换句话说就是新的结点必须与已有的结点都相关。

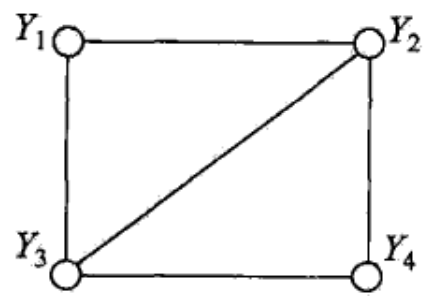
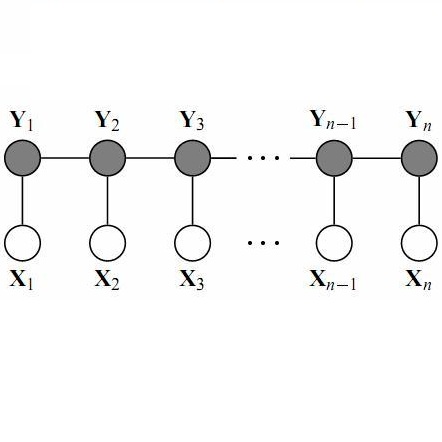
下图是《统计学习方法》中的例子，根据上面的定义，我们可以很容易地得到图中有两个最大团{Y1，Y2，Y3}，{Y2，Y3，Y4}

所以由之前的定理可知：

$$ P\left( Y \right) = \frac{1}{Z}\Psi(Y_{1},Y_{2},Y_{3})\Psi(Y_{2},Y_{3},Y_{4}) $$

在条件随机场中，该定理就变为了如下形式：

$$ P\left( Y_{v}|X,Y_{w},w \neq v \right) = P\left( Y_{v}|X,Y_{w},w \sim v \right) = \frac{1}{Z}\prod_{C}{}{\Psi_{c}(Y_{c}|X)} $$

乘法总是难算的而加法总是亲切的，因此通常我们会令

$$ \Psi_{c}(Y_{c}|X)=e^{\text{λf}(X,\text{Yc})} $$

于是乘法变成了加法，我们也得到了条件随机场的参数化形式。

条件随机场的参数化形式：

设P(Y|X)为条件随机场，则在随机变量X取值为x的情况下，随机变量Y取值为y的条件概率具有如下形式

$$ P\left( y|x \right) = \frac{1}{Z}e^{\sum_{}{}{\text{λf}(x,\text{yc})}} $$

$$ Z = \sum_{Y}^{}e^{\sum_{}^{}{\text{λf}(x,\text{yc})}} $$

这里$f(x,\text{yc})$是特征函数，所谓特征函数，就是指明特征的函数，当输入满足一定特征时（例如这里的X=x，Yc=yc），输出为1，否则输出为0.

看起来是不是很厉害？其实只是最简单的条件概率分布的变形而已，通过这个式子，我们给各种所需的情形分配了一个参数λ，但不考虑归一化项，不过是令$P\left( \text{yc}|x \right) = e^{\lambda}$罢了。求解参数的过程和求条件概率分布并没有本质上的区别。

当然，本质上虽然没有区别，形式上却是方便了许多，我们在求解的时候只要枚举出所有的特征函数，再求出所有的参数λ，就可以了——这就是条件随机场的简化形式。

CRF的简化形式：令W=(w1,w2,……)T，F(x,y)=(f(x,yc1), f(x,yc1),……)，则条件随机场可以写成向量的内积形式：

$$ P_{w}\left( y|x \right) = \frac{1}{Z_{w}}e^{W*F(x,y)} $$

其中：$Z_{w} = \sum_{y}{}e^{W*F(x,y)}$

对于线性链条件随机场，也可以写成矩阵乘积的形式。

条件随机场的矩阵形式：除了原始的下标1，2，3，……，n，为了方便计算和表示，引入两个特殊的起点和终点标记：$start=y_0$，和$stop=y_{n+1}$

设y有m种不同的可能取值，对观测序列x的每一个位置i=1,2,3,…,n，定义一个m阶矩阵Mi：

$$ M_{i} = \lbrack M_{i}(y_{i - 1},y_{i}|x)\rbrack $$

$$ M_{i}\left( y_{i - 1},y_{i}|x \right) = e^{\text{WF}(x,y_{i - 1},y_{i})} $$

这里M种的第a行第b列元素，对应着$y_{i - 1} = a$，$y_{i} = b$，时的结果。

根据这一定义，我们可得，条件概率$P_{w}\left( y|x \right)$为：

$$ P_{w}\left( y|x \right) = \frac{1}{Z_{w}}\prod_{i = 1}^{n + 1}{M_{i}(y_{i - 1},y_{i}|x)} $$

其中归一化因子Zw为：

$$ Z_{w} = \prod_{i = 1}^{n + 1}M_{i} $$

这一形式不用细究，我们会在后面的应用中逐步理解。

虽然花了不少篇幅来详细阐述CRF是什么，不过在实际应用中我们并不需要想那么多，除了某些特殊情形外，基本上直接用CRF的简化形式即可。

介绍完了定义，接下来开始解决概率图模型都存在的三个经典问题：

1）概率计算问题，已知模型中的各种参数，求解模型中的各种概率分布

2）学习问题，已知一堆训练数据，如何通过学习得到模型中的各种参数

3）预测问题，已知模型中的各种参数以及输入向量，求解输出向量

Reference：

《统计学习方法》李航

https://www.zhihu.com/question/20380549/answer/45066785 宁远成梁

https://zhuanlan.zhihu.com/p/26696451