FOCS 2019重磅来袭，清华姚班毕业生陈立杰连中三元

---

  新智元推荐  

来源：会议之眼

【新智元导读】 深度学习大神、亚马逊AI主任科学家李沐此前便是顶会FOCS获奖者，今年FOCS,MIT博士生、清华姚班毕业生陈立杰今年一连中奖3篇，并荣获最佳学生论文奖。来新智元 AI 朋友圈与AI大咖一起讨论吧～

会议之眼A类、CCF A类会议FOCS（Foundations of Computer Science）是由IEEE计算机协会计算数学基础技术委员会主办的国际顶会！大会致力于为计算机理论的基础研究和新方法开创领域的研究者提供一个交流和展示的平台。其高逼格、难搞定的程度让不少科研工作者只得仰望。深度学习大神、亚马逊AI主任科学家李沐此前便是FOCS获奖者，而MIT博士生、清华姚班毕业生陈立杰今年一连中奖3篇，并荣获最佳学生论文奖。

FOCS每年举办一次，第60届计算机科学基础IEEE研讨会定于2019年11月9日至12日在美国马里兰州最大城市巴尔的摩召开。论文提交截止日期为同年4月5日，接收公布日期为7月1日。小程序会议之眼plus提供了会议时间、地点、等级和官网查询地址。致力于在计算机基础理论研究领域发Paper的小伙伴要早做规划，及时收藏呀！

论文主题涵盖算法和数据结构、计算复杂度、密码学、经济学、并行和分布式算法、量子计算、计算生物学和数据库等主题。本届大会共计评选出3篇最佳论文和2篇最佳学生论文。会议之眼独家解读，带您一窥计算机基础研究的世界（PS:文章已整理，关注公众号回复focs2019 即可获取）。

最佳论文

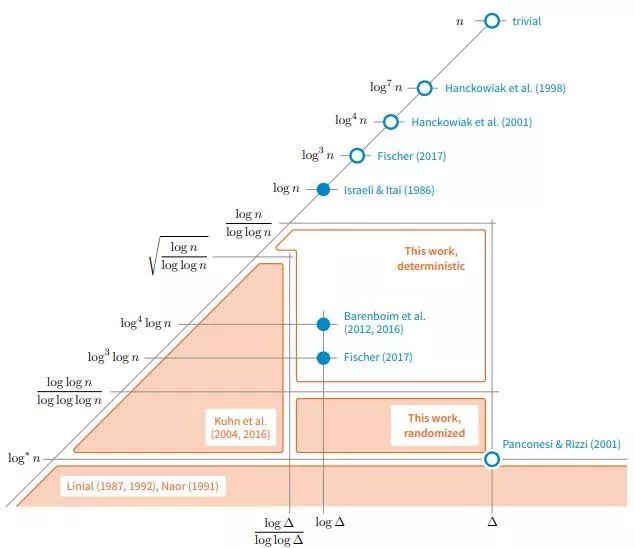
Lower bounds for maximal matchings andmaximal independent sets

Alkida Balliu,Sebastian Brandt,JuhoHirvonen,Dennis Olivetti,Mikaël Rabie, Jukka Suomela

论文简介：

在O（Δ+ log ∗ n）的通信回合中，存在用于找到最大匹配和最大独立集的分布式图形算法。这里n是节点数，Δ是最大度。Linial的下限表明对n的依赖是最优的：即使Δ= 2，这些问题也无法在O（Δ+ log ∗ n）轮中解决。但是，对Δ的依赖性是一个长期存在的悬而未决的问题，目前在上下限之间存在指数差距。

作者证明上限是紧密的。在分布式计算的本地模型中，使用任何随机算法都无法在O（Δ+ loglogn / logloglogn）轮次中找到最大匹配和最大独立集。因此，没有一个确定的算法可以在O（Δ+ logn / loglogn）轮次中运行最大匹配或最大独立集。这可以作为n的函数对先前的下限进行改进。

NEEXP⊆ MIP*

Authors: AnandNatarajan,John Wright

论文简介：

作者研究了multiprover交互式证明系统。证明了经典的multiprover交互证明系统的作用，其主要结果是等式MIP = NEXP。事实证明，量子多重证明者交互式证明系统的功能难以证明，其中证明者可以共享纠缠。Ito和Vidick曾提出了MIP *的最著名下限是NEXP。至于上限，MIP *可以和RE一样大。

这项工作的主要结果是在提出了MIP *的NEEXP（不确定的双指数时间）。这是对先前下限的一个指数改进，表明具有纠缠证明者的证明系统至少比经典证明者在指数上具有更大的功能。在作者的协议中，验证者将经典的NEEXP，指数上的MIP协议委派给两个纠缠证明者：证明者通过测量其共享状态来获得其指数问题，并使用经典PCP来证明其答案的正确性。至关重要的是协议的稳健性，每个参与者不仅应该正确地对自己的问题进行抽样，而且还应避免会泄露其他参与者的抽样问题的情况出现。

Automating Resolution is NP-Hard
Albert Atserias,Moritz Müller

论文简介：

作者发现驳斥解决的问题在于非确定性多项式复杂度的归约问题。在证明复杂性方面，除非P = NP，否则解决方案无法自动执行。区分具有多项式长度的分辨率反驳的公式和不具有次指数长度反驳的公式是非确定性多项式复杂度的归约问题。这也意味着，除非在SUBEXP或QP中分别包含NP，否则分辨率无法在指数以下的时间或准多项式时间内自动执行。

最佳学生论文

EfficientConstruction of Rigid Matrices Using an NP Oracle

Josh Alman, Lijie Chen

 

Faster Minimum k-cut of a Simple Graph

Jason Li

小助手已经打包整理好上述文章，关注计算机科学基础研究的朋友们快快收藏起来! 阅读顶会最佳论文，关注最新动态！

如何获取论文合集？在微信公众号“会议之眼”对话框中回复“focs2019”即可获得~