系列3 | CV领域这样入门进阶才是对滴

新年倒计时 3 天

2月的第一天，回首远望，发现2019我们已经走过了1/12分之一，不知道你们新年的一个月里有了多少收获了呢?

没关系！！！

现在开始，我们一起学习一会吧，不能因为假期而停歇科研的精神，在娱乐（农药&吃鸡）疲劳之间隙，可以和我们一起来简单的学习（真的不用太费脑）

开个小差，可以扫上面的“福"哦，可收集五福哦！

           今天我们学习啥呢？

  今天绝对干货，要认真看哦~

图像处理基本算法

01

图像分辨率降低处理

如果，你手中有一张256*256分辨率的图像，想让它降低为128*128分辨率，可以将源图像划分成2*2的子图像块，然后将2*2的子图像块的所有像素颜色均按照F(i,j)的颜色值进行设定，达到降低分辨率的目的。

案        例

F(i,j)    F(i,j+1)

F(i+1,j)  F(i+1,j+1) 

 变成

F(i,j)  F(i,j)

F(i,j)  F(i,j)

同样的道理，只要你知道这样的应用，就可以把256*256分辨率的图像变成任意分辨率大小，比如变成64*64的分辨率，只需要划分成4*4即可，以此类推。

02

图像单色化处理及亮度、色差和信号值关系

如果，你想把彩色图像变成单色图像，想一想应该能够很简单得出答案！

RGB彩色图像，你只需要将图像的每一个像素中相对应的R, G, B值取出，然后利用(R,R,R),(G,G,G),(B,B,B)的像素重新绘制即可。

在图像中，彩色图像的亮度Y，色差I，信号值Q的关系，应该要理解：

| Y |    |0.31  0.59  0.11   |    | R |
| I | =  |0.60 -0.28  -0.32 | * | G |
|Q |     |0.21  -0.52 -0.31 |    | B |

也就是一个矩阵的乘法，结果如下：

Y = 0.31R + 0.59G+0.11B

I  = 0.60R - 0.28G - 0.32B

Q = 0.21R - 0.52B - 0.31B

03

图像的滤波处理

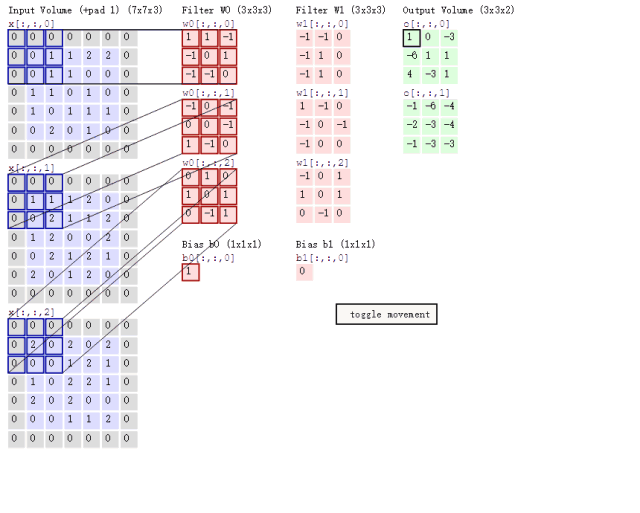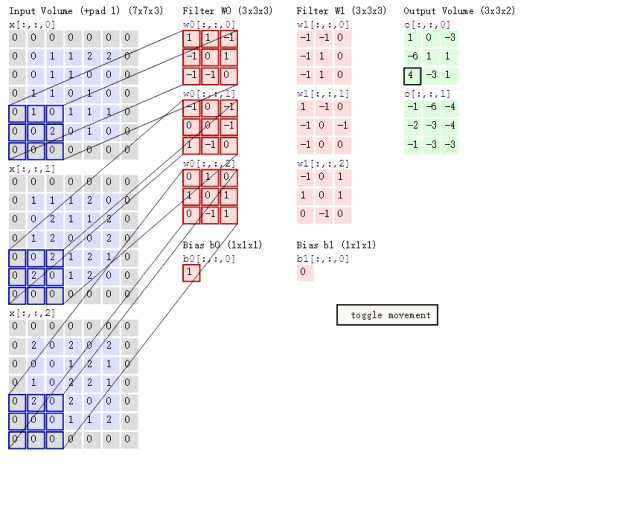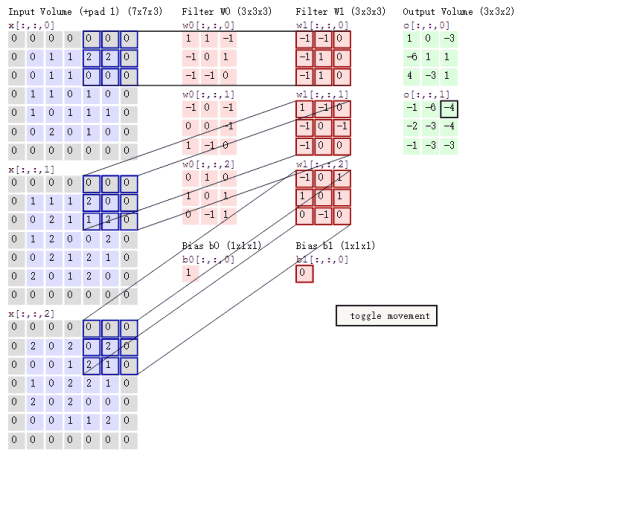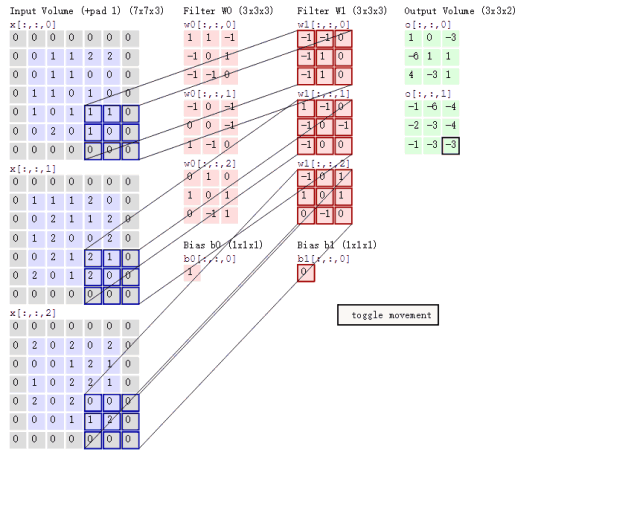
实际上，在信号处理这个领域中卷积还有广泛的意义。2D卷积需要4个嵌套循环4-double loop，所以它并不快，除非我们使用很小的卷积核。这里一般使用3x3或者5x5。而且，对于滤波器也有一定的规则要求：

· 滤波器的大小应该是奇数，这样它才有一个中心，有中心也就有了半径，例如5x5大小核的半径就是2；

· 滤波器矩阵所有的元素之和应该要等于1，这是为了保证滤波前后图像的亮度保持不变，不按照这个要求也是可以的；

· 如果滤波器矩阵所有元素之和大于1，那么滤波后的图像就会比原图像更亮，反之，得到的图像就会变暗，如果和为0，图像不会变黑，但也会非常暗；

· 对于滤波后的图像，可能会出现负数或者大于255的数值，对于这种情况，将他们直接截断到0和255之间即可，对于负数，可以取绝对值。

图像处理实践

01

无任何处理

02

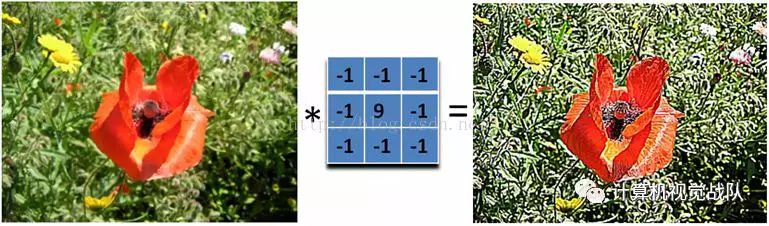
图像锐化

图像的锐化和边缘检测非常相似，首先要找到图像的边缘，然后把边缘加到原图像上，这样就强化了图像的边缘，使图像看起来更加锐利。

这两者操作统一起来就是锐化滤波器了，也就是在边缘检测滤波器的基础上，再在中心的位置加1，这样滤波后的图像就会和原始的图像具有同样的亮度了，但是会更加锐利，如下：

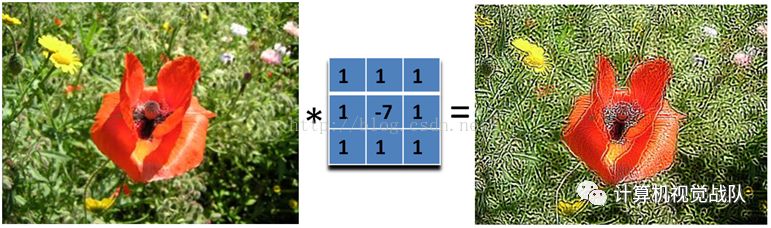
下面的滤波器会更强调边缘：

03

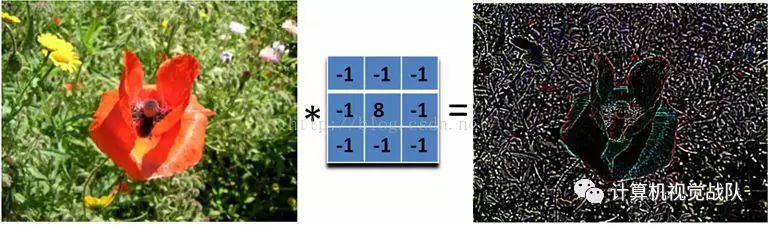
边缘检测

在模式识别时，检测出图像边缘或者抽出图像轮廓是最常用的操作。迄今为止，已经出现了许多成熟的算法。

例如微分算法，掩模算法等。在微分算法中，常使用N*N的像素块，例如3*3的像素块如下：

f(i-1,j-1)  f(i-1,j)  f(i-1,j+1)

f(i,j-1)     f(i,j)      f(i,j+1)

f(i+1,j-1) f(i+1,j)  f(i+1,j+1)

设f(i,j)为待处理的像素，而g(i, j)为处理后的像素。

Roberts算子

g(i, j) = sqrt( (f(i, j) - f(i + 1, j))^2 + (f(i + 1, j) - f(i, j + 1))^2 )

或 g(i, j) = |f(i,j) - f(i + 1,j)| + |f(i+1,j) - f(i,j+1)|

Sobel算子

对数字图像的每一个像素f(i,j),考察它的上、下、左、右邻域灰度的加权值，把各方向上(0度、45度、90度、135度)的灰度值加权之和作为输出，可以达到提取图像边缘的效果，即 g(i,j) = fxr + fyr，其中：

fxr = f(i-1,j-1)+2*f(i-1,j)+f(i-1,j+1)-f(i+1,j-1)-2*f(i+1,j)-f(i+1,j+1)

fyr = f(i-1,j-1)+2*f(i,j-1)+f(i+1,j-1)-f(i-1,j+1)-2*f(i,j+1)-f(i+1,j+1)

Laplace算子

Laplace算子是一种二阶微分算子。它有两种形式: 4邻域微分算子和8邻域微分算子。

• 4邻域微分

g(i,j)=|4*f(i,j)-f(i,j-1)-f(i-1,j)-f(i+1,j)-f(i,j+1)|

• 8邻域微分

g(i,j)=|8*f(i,j)-f(i,j-1)-f(i-1,j)-f(i+1,j)-f(i,j+1)-f(i-1,j-1)-f(i-1,j+1)-f(i+1,j-1)-f(i+1,j+1)|

04
04

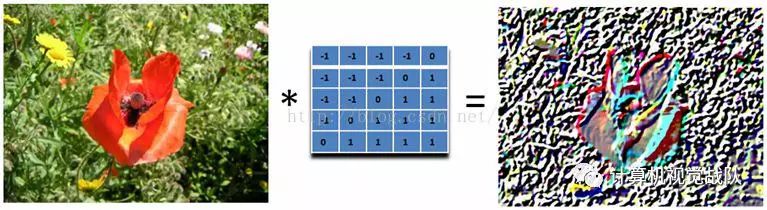
浮  雕

以下是45°的浮雕，并且加大滤波器效果如下：

05

高斯模糊

所谓"模糊"，可以理解成每一个像素都取周边像素的平均值。

"中间点"取"周围点"的平均值，就会变成1。在数值上，这是一种"平滑化"。在图形上，就相当于产生"模糊"效果，"中间点"失去细节。显然，计算平均值时，取值范围越大，"模糊效果"越强烈。

上面分别是原图、模糊半径3像素、模糊半径10像素的效果。模糊半径越大，图像就越模糊。从数值角度看，就是数值越平滑。

部分内容摘自于”丑着睡不着“的CSDN内容！感谢~

完

下一期我们会详细说说灰色图像的基本处理及算法，在此提前祝阅读的您新年快乐！

往期回顾

/计算机视觉入门——1

新手看过来，入门阅读请点击左图！

/计算机视觉入门——2

入门进一步阅读请点击左图！