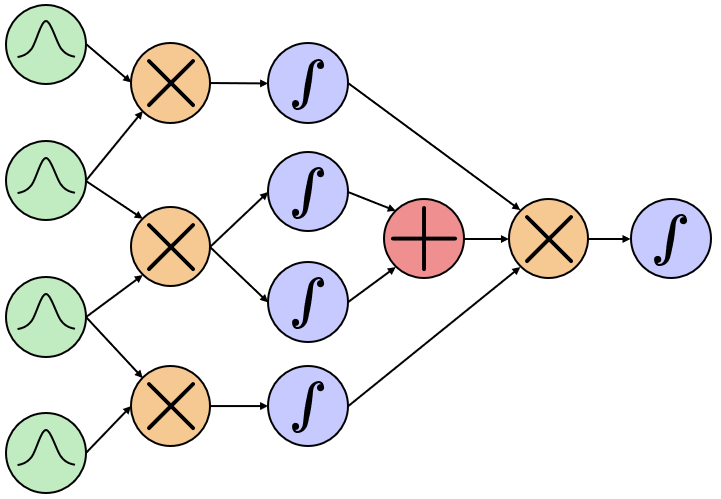
概率积分电路(PICs)最近被提出作为一种概率模型,具备表达能力强的生成模型背后的关键要素:连续潜在变量(LVs)。PICs 是符号化的计算图,将连续 LV 模型定义为函数层次结构,这些函数通过相加和相乘,或者对某些 LV 进行积分而构成。如果可以解析地积分出 LV,则它们是可解的,否则可以通过称为 QPCs 的可解概率电路(PC)来近似,该电路编码了分层数值求积过程。到目前为止,只有树状的 PICs 被探索过,而通过数值求积训练它们在大规模下需要大量内存处理。本文中,我们解决了这些问题,并提出了:(i) 从任意变量分解构建有向无环图(DAG)形状的 PICs 的流程,(ii) 使用张量化电路架构训练 PICs 的方法,以及 (iii) 神经功能共享技术以实现可扩展的训练。在广泛的实验中,我们展示了功能共享的有效性以及 QPCs 相较于传统 PCs 的优越性。
成为VIP会员查看完整内容