【论文笔记】用于深度时空图建模的Geaph WaveNet
导读

论文链接:
https://arxiv.org/pdf/1906.00121.pdf
时空图建模背后的基本假设是,节点的未来信息取决于其历史信息以及其邻居的历史信息。因此,如何同时捕获空间和时间依赖性成为时空图建模的主要挑战。而之前将图卷积网络(GCN)集成到循环神经网络(RNN)或卷积神经网络(CNN)中的时空图建模方法面临如下两个主要缺点:
1)数据的图结构并不能反映节点之间真正的依赖关系。存在连接并不意味着两个节点之间存在相互依赖关系;两个节点之间存在相互依赖关系却缺少连接。
2)先前基于RNN与CNN的方法都需要很多层才能捕获长序列的时间依赖性,并且随着层数的增加RNN存在梯度爆炸、消失的问题。
基于以上缺点,文中提出了一个Graph WaveNet框架,使用可以通过端到端训练从数据中学习自适应邻接矩阵(self-adaptive adjacency matrix)的图卷积层,来捕获隐藏的空间依赖性。采用堆叠的dilated casual (空洞因果)卷积来捕获时间依赖性。
Graph WaveNet将具有自适应邻接矩阵的图卷积层与dilated casual (扩张因果)卷积结合起来,同时捕获时空依赖性。Graph WaveNet的框架如下图所示,是由堆叠的k个时空层(spatial-temporal)和输出层组成。
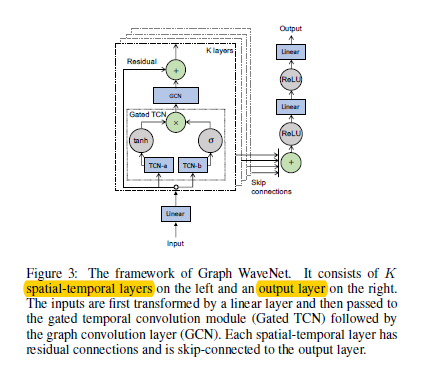
时空层由图卷积层(GCN)和门控时间卷积层(Gated TCN)构成,每个图卷积层都可以得到由dilated casual (空洞因果)卷积层在不同粒度级别提取的节点信息的空间依赖性。通过堆叠多个时空层,Graph WaveNet能够处理在不同时间级别的空间依赖性,在底层,GCN接收短期时间信息,而在顶层GCN处理长时间信息。
问题设置
给定图G及其历史S步图信号,目标是能够学习得到预测其下一个T步图信号的函数f。映射关系表示如下:
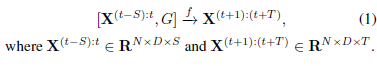
其中:
G = (V,E)表示图
V是节点的集合、E是边的集合。
A ∈R表示邻接矩阵,如果v_i、v_j ∈V,并且当(v_i、v_j )∈E时,A_{ij}为1,否则为零。
X^(t) ∈R表示t时刻的图信号
图卷积层
给定节点的结构信息,图卷积是提取节点特征的重要操作。文中的图卷积层是基于Li 等人提出的扩散卷积层上的改进。文中提出了一个自适应邻接矩阵~A_adp。这个自适应邻接矩阵不要需要任何的先验知识就可以通过随机梯度下降(SGD)来进行端到端的学习。
丨点击DCRNN查看Li 等人提出的扩散卷积
自适应邻接矩阵
文中通过随机初始化两个具有可学习参数E_1、E_2∈R^(N*c)的节点嵌入字典来实现此目的。自适应邻接矩阵定义为:
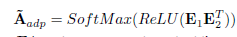
图卷积层
通过结合预定义的空间依赖关系和自学习的隐藏图依赖关系,图卷积层可以表示为:
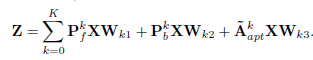
其中:
P^k表示状态转移矩阵的幂级指数
P^k=(D^(-1)A)^k
在有向图中,扩散的进程有两个方向,前向传播方向与反向传播方向。当图结构不可用时,可以仅使用自适应邻接矩阵来捕获隐藏的空间依赖关系,即:
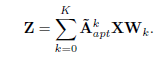
文中提出的图卷积可以被解释为聚集来自不同邻域的变换后的特征信息。
时间卷积层
文中采用dilated casual (空洞因果)卷积作为时间卷积层(TCN)去捕获节点的时间趋势。空洞因果卷积神经网络允许通过增加层的深度来获得一个指数级的感受野(receptive field)。
空洞因果卷积(dilated casual )
与基于RNN的方法不同的是,空洞因果卷积神经网络能够以非递归的方式正确处理长序列,这样便于并行计算并且缓解梯度爆炸问题。
空洞因果卷积通过将0填充到输入中保存时间因果顺序,以便在当前时间步长上进行的预测仅涉及历史信息。空洞因果卷积通过按一定的步长跳过一定的值在输入上滑动,如图2所示。
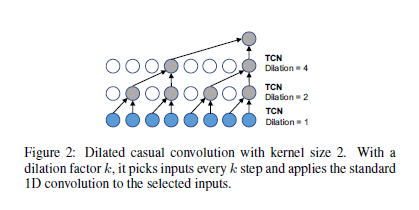
给定一个一维输入序列x∈R^k,x与 f 在时间t处的空洞因果卷积运算表示为:
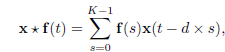
其中:
d表示空洞向量,控制跳的距离。
通过将空洞因果卷积层按空洞因子d递增的顺序堆叠,模型的感受野呈指数级增长。这样使得空洞因果卷积神经网络能够用更少的层捕获长序列,节约了计算资源。
Gated TCN
门控(Gating)机制证明对时间卷积网络的层间信息流具有很强的控制作用,文中采用Gated TCN来学习复杂的时间依赖性。
给定一个输入X ∈R^(N×D×S),它的表示形式如下:
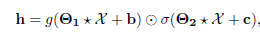
其中:
Θ_1、Θ_2、b和c是模型参数
⊙是按元素相乘
g(.)是输出的激活函数,选择切线双曲函数
σ(.)是sigmod函数决定信息传到下一层的比例。
训练
文中选择使用平均绝对误差(MAE)作为Graph Wave Net的目标函数:
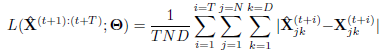
与先前工作不同的是,GraphWaveNet的输出~X^((t+1):(t+T))是一个整体而不是递归的通过t步产生~X^(t)。它解决了在训练和测试中由于由于模型学习在训练期间对一个步骤进行预测,并且预期在推断过程中对多个步骤产生预测的不协调问题。
数据集
文中使用与DCRNN一样的两个公共交通网络数据集Metr-la和Pems-Bay。
Metr-la:记录了洛杉矶县高速公路上207个传感器上四个月的交通速度统计数据。
Pems-Bay:包含在湾区325个传感器上6个月的交通速度信息。
数据集按时间顺序划分,70%用于训练,10%用于验证,20%用于测试。下表为详细的数据分布情况:

实验设置
神经网络层数:8
空洞因子:1; 2; 1; 2; 1; 2; 1; 2.
GCN模块中扩散(diffusion)步长K:2
学习率:0.001
Dropout的比率:0.3
评价指标:平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)
Baseline: ARIMA、FC-LSTM、WaveNet、DCRNN、GGRU、STGCN
实验结果
为了证明Graph WaveNet的有效性,文中比较了Graph WaveNet和baseline模型15分钟、30分钟和60分钟对Metr-la和Pems-Bay数据集的预测性能,如表2所示:
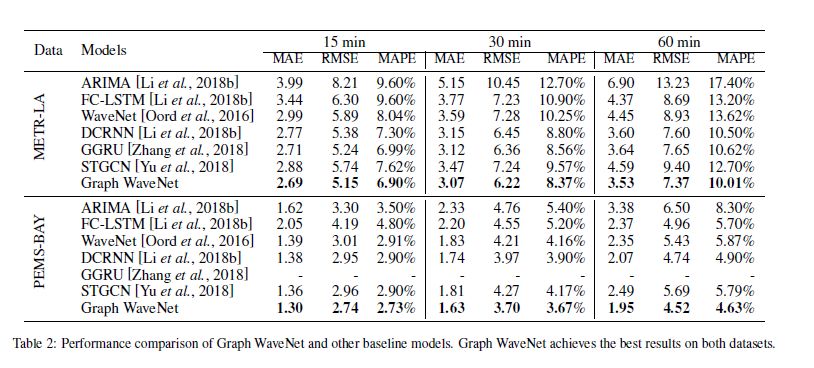
从表中,可以看到与其他时空模型相比,Graph Wave NET 明显优于以往基于卷积的方法 STGCN,同时优于基于递归的方法DCRNN和GGRU。这些改进都归因于Graph WaveNet 包含具有不同参数的单独的GCN层。
为了验证文中提出的自适应邻接矩阵的有效性,作者利用Graph WaveNET的五种不同的邻接矩阵配置进行了实验,如表3所示:
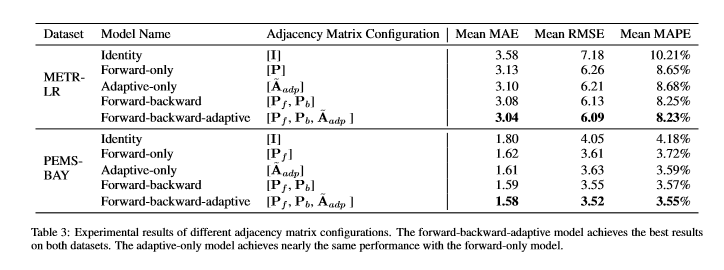
从表中可以知道,增加自适应邻接矩阵可以为模型引入新的有用信息。
Graph WaveNet 是一种新的时空图建模模型.该模型通过将图卷积和空洞因果卷积相结合,有效地捕捉了时空依赖关系.是一种从数据中自动学习隐藏空间依赖关系的有效方法。






