【干货】深度学习中的数学理解— 教你深度学习背后的故事- 专知

【干货】深度学习中的数学理解— 教你深度学习背后的故事

【导读】如今，深度学习在各项任务中所向披靡，比如图像识别，语音处理和自然语言处理。但是，深度学习的理论探讨却比应用滞后好几个数量级，一方面是做应用马上能见效，然后会有很多人尝试，另一个方面是做理论研究门槛相对比较高。本文是ICCV 2017上《深度学习中的数学理解》（Tutorial on the Mathematics of Deep Learning）教程的论文总结，从网络架构、正则化技术和优化算法三个方面解释深度学习成功背后的数学理论支撑，并详细讲解全局最优性、几何稳定性、学习表征不变性等网络特性的数学解释。

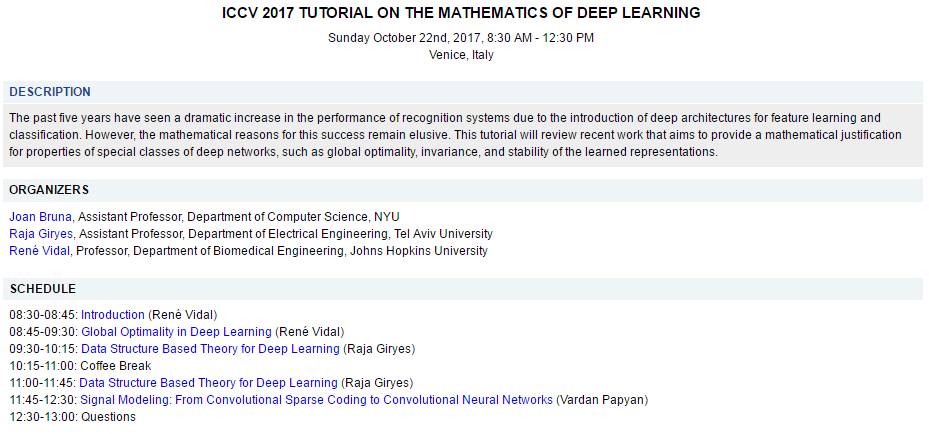
参考链接：http://www.vision.jhu.edu/tutorials/ICCV17-Tutorial-Math-Deep-Learning.htm

▌相关资源汇总

1. ICCV 2017 Tutorial on the Mathematics of Deep Learning

http://www.vision.jhu.edu/tutorials/ICCV17-Tutorial-Math-Deep-Learning.htm

2. 演讲PPT

Global Optimality in Deep Learning (René Vidal)
http://www.vision.jhu.edu/tutorials/ICCV17-Tutorial-Math-Deep-Learning-Rene.pdf
Data Structure Based Theory for Deep Learning (Raja Giryes)
http://www.vision.jhu.edu/tutorials/CVPR17-Tutorial-Math-Deep-Learning-Raja.pdf
Signal Modeling: From Convolutional Sparse Coding to Convolutional Neural Networks (Vardan Papyan)
Signal Modeling: From Convolutional Sparse Coding to Convolutional Neural Networks

▌演讲视频

https://v.qq.com/x/page/a0522c99b9q.html

https://v.qq.com/x/page/t0522yueuec.html

▌论文

Mathematics of Deep Learning （深度学习中的数学）

作者：René Vidal、Joan Bruna、Raja Giryes、Stefano Soatto

▌摘要

最近，由于表示学习和分类的深层架构的引入，识别系统的准确度有了巨大的提升。但是，其中包含的数学原理仍然是晦涩难懂的。这篇教程将会回顾最近的相关工作，旨在为深度学习网络的一些特性提供数学层面的证明。例如，全局最优性，几何稳定性以及表示学习的不变性。

▌介绍

深度网络是对输入数据执行序列操作的参数化模型。每个这样的操作，通俗地称为“层”，由线性变换组成，例如它输入的卷积，紧接着跟着的是一个逐点的非线性的“激活函数”，像sigmoid这样的函数。深度网络最近在语音，自然语言处理以及计算机视觉等各种应用中的分类性能有了显著地提高。与传统的神经网络相比，深度网络被认为有如此优异表现的关键是其拥有大量的“层”。但是它还有其他结构上的调整，比如修改了的线性激活函数（ReLUs）以及残差的 ‘快捷’ 连接。表现优异的其他主要因素还有可用的海量数据集，比如说像ImageNet这种有着数以百万计图像的数据集。同时还有高效的GPU计算硬件的支持，解决了高达一个亿的参数的高维优化问题。

深度学习，尤其是卷积神经网络（CNNs）在基于图像的任务上很成功，给理论学家们带来了许多难题。特别是在深度学习中有三个关键要素，即体系结构、正则化技术和优化算法，这些对于训练一个理想的深度网络是至关重要的。如果想要知道深度网络为什么表现地如此优异，理解这三个要素以及它们之间的相互作用是很有必要的。

A. 近似、深度、宽度和不变性

神经网络结构设计中的一个重要特性是它能够近似地估计输入的任意函数。但是，这种能力的好坏取决于体系结构的参数，比如神经网络的深度和宽度。早期的研究表明，带有一个隐藏层和sigmoid型激活函数的神经网络是通用的函数逼近器。然而，一个宽而浅的网络的所能容纳的数据可以复制到一个深度的网络，并且在性能上有显著的改进。为什么性能会提升，一种可能的解释是，与浅层网络相比，较深的体系结构能够更好地捕获数据的不变性。例如，在计算机视觉中，对一个物体的分类是不受视点，光照等因素的影响的。然而最初对于为什么深层网络能够捕捉这种不变性的数学分析是难以达到的，最近的一些研究进展为深层网络的某些子类别阐明了这个问题。特别地，散射网络9是深度网络的一种，其卷积滤波器由复杂的多分辨率小波族给出。这种额外的特殊结构是可证明的稳定和局部不变的信号表示，并揭示了几何和稳定性在支撑现代深层卷积网络体系结构的泛化性能中的基础作用。详见第四部分。

B. 泛化和正则化特性

神经网络体系结构的另一个关键特性是它能够从少量的训练示例中进行泛化。统计学习理论的传统结果10表明，要达到良好的泛化需要的训练样本的数量会根据网络的大小而多项式地增长。然而，在实际操作中，深度网络的训练数据要比其参数数量少得多(N远小于D)，但是它们可以使用非常简单（看似适得其反）的正则化技术来防止过度拟合，比如Dropout11，它通过在每次迭代中冻结一个随机的参数子集。

对于这个谜题（深度网络为什么可以从少量训练数据中泛化），一个可能的解释是，更深层次的体系结构会产生一个输入数据的嵌入，它近似地保留了同一类数据点之间的距离，同时增加了类之间的间隔。本教程将概述12最近的工作，它使用压缩感知和字典学习的工具来证明，具有随机高斯权重的深度网络对相似输入具有相似输出的数据执行了一种保持距离的数据嵌入。这些结果提供了对网络的度量学习属性的洞察，并导致了由输入数据结构所告知的泛化误差的界限。

C. 信息理论属性

网络架构的另一个关键特性是它能够产生良好的“数据表示”。粗略地说，一个表示是对一个任务有用的输入数据的任何函数。一个最佳的表示形式是“最有用”的量化，例如，通过信息理论、复杂性或不变性标准13进行量化。这类似于系统的“状态”，是一个代理将这种“状态”存储在内存中以代替数据去预测未来的观察值。例如，卡尔曼滤波器的状态是预测由高斯噪声线性系统产生的数据的最优表达式;换句话说，它是预测的最小充分统计量。对于复杂的任务，数据可能被不包含任务信息的“nuisances”损坏，也可能希望这种表示是“不变的”，以避免影响未来的预测。一般来说，任务的最优表示可以定义为充分的统计数据(过去的或者“训练”数据)，这同时也是最小的，并且对“nuisance”变量是不变的，这影响着未来(“测试”)数据14。尽管对表征学习有很大的兴趣，但是一个全面的解释了深层网络作为构造最优表征性能的理论还不存在。事实上，即使是充分性和不变性等基本概念也得到了不同的处理9, 14, 15。

最近的工作16, 17, 18已经开始为深层网络所学习的表征建立信息理论基础。其中包括对信息瓶颈损失13的观察，它定义了一个不严格的最小充分性概念，可用于计算最优表示。信息瓶颈损失可以重新写为交叉熵项的总和，这是深度学习中最常使用的损失，还有一个额外的正则化项。后者可以通过在学习表征中引入类似于自适应丢失噪声的噪声来实现17。由此产生的正则化形式，即17中所称的信息丢失，显示了在资源约束条件下的改进学习，可以被显示并导致“maximally disentangled”表示，也就是说，表示的组成部分之间的（总）相关性是最小的，从而使得特征指标具有独立的数据特性。此外，类似的技术也证明了对抗扰动18的鲁棒性提高了。因此，信息理论将在形式化和分析深层表征的性质以及提出新类型的正则化工具方面起着关键作用。

D. 优化性能

训练神经网络的经典方法是利用反向传播19（一种专门用于神经网络的梯度下降法）使（正则化的）损失最小化。反向传播的现代版本依靠随机梯度下降（SGD）来高效逼近海量数据集的梯度。虽然SGD只是对凸损失函数进行严格分析20，但在深度学习中，损失是网络参数的非凸函数，因此不能保证SGD找到全局最小值。

实践中，有大量证据表明，SGD经常为深度网络提供良好的解决方案。最近有关理解训练质量的研究表明，临界点更可能是鞍点而不是假的局部极小值21，局部最小值集中在全局最优点附近22。最近的研究还发现，SGD发现的局部极小值导致了良好的泛化误差，属于参数空间非常平坦的区域23。这激发了像Entropy-SGD这样的算法，这些算法专门用来寻找这样的区域，并从统计物理中的二进制感知器分析中得出类似的结果24。他们已经被证明在深度网络上表现良好25。令人惊讶的是，这些来自统计物理学的技术与偏微分方程（PDE）的正则化性质密切相关26。例如，局部熵，Entropy-SGD的最小化的损失，是Hamilton-Jacobi-Bellman偏微分方程的解，因此可以写成随机最优控制问题，惩罚贪婪（greedy）梯度下降。这个方向进一步导致具有良好的经验性能的SGD的变体与标准方法在凸优化(如infconvolutions和近端方法)之间的联系。研究人员现在才刚刚开始揭示深度网络在其拓扑结构上的损失函数，这就决定了优化的复杂性以及它们的几何结构，这似乎与分类器的泛化特性有关27,28 29]。

本教程将概述最近的工作，显示高维非凸优化问题，如深度学习的误差面具有一些良性的性质。例如，30，31的工作表明，对于某些类型的神经网络，其损失函数和正则化函数都是相同程度的正齐次函数的和，在局部最优的情况下，它的许多项是零，从而也是全局最优的。这些结果也将为RELUs这类正齐次函数的成功提供一个可能的解释。这个框架的特殊情况包括，除了深度学习之外，还有矩阵分解和张量因子分解32。

E. 论文大纲

本文的其余部分组织如下。第二节描述了深度网络的输入-输出图。第三节研究深度网络的训练问题，为全局最优性创建了条件。第四节研究了散射网络的不变性和稳定性。第五节研究深度网络的结构特性，如嵌入的度量属性以及泛化误差的界限。第六节研究了深度表征的信息理论性质。

参考文献：

http://www.vision.jhu.edu/tutorials/ICCV17-Tutorial-Math-Deep-Learning.htm

http://www.vision.jhu.edu/tutorials/CVPR17-Tutorial-Math-Deep-Learning.htm

http://www.vision.jhu.edu/tutorials/CVPR17-Tutorial-Math-Deep-Learning-Intro-Rene.pdf

https://arxiv.org/abs/1712.04741

▌特别提示-论文最新下载

请关注专知公众号（扫一扫最下面专知二维码，或者点击上方蓝色专知），