用Python中可视化梯度下降

【导读】你是否好奇在训练神经网络的时候梯度是如何下降的？ 怎样设计梯度下降的策略才能够使模型更快收敛？ 这篇博客可视化了梯度下降的方法，并直观表明，当损失表面一个方向比其他方向陡峭时（raven-like），与动量相比，具有动量的梯度下降可以更快地收敛。

作者｜Henry Chang

编译｜专知

整理｜Yingying，李大囧

从简单的开始

让我们从设定一个raven-like 损失函数并将其投影到二维开始。

L（x，y）= 1 /16x²+ 9y²

下图是raven-like损失函数。 对于该损失表面，在点（0,0）处存在全局最小值，其值等于零。

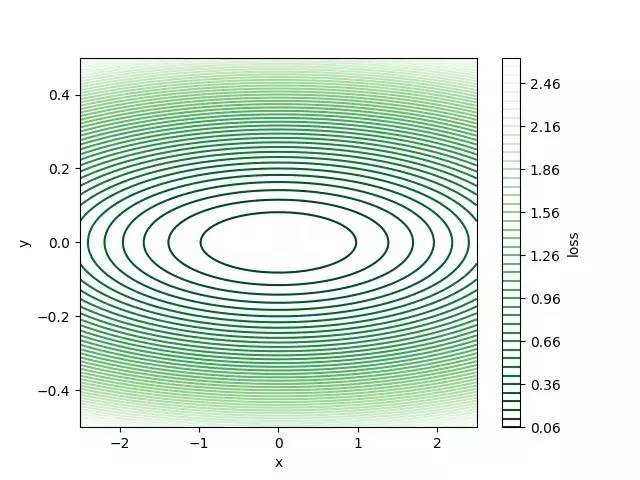
具有动量的梯度下降

梯度下降是一种优化算法，可以找到给定函数的最小值。在机器学习中，我们使用梯度下降来减小损失。vanilla梯度下降的问题在于某些损失表面的收敛时间很长，其中一个技巧是使用动量来达到更快的收敛。

动量方法可以在梯度指向跨越迭代的相同方向的方向上累积速度。它通过将当前权重更新的一部分添加到当前权重更新来实现此目的。我们首先展示动量的数学原理，然后进行一些实验，看动量是否真的能帮助我们实现更快的收敛。

下面的等式是具有动量更新的梯度下降。 β是添加的动量部分的权值，范围为0~1。当β= 0时，它会退化到到vanilla梯度下降。

v =βv+∇L（w）

w = w - αv

我们首先在初始化我们的权重（-2.4,0.2）。接下来，尝试使用学习率α= 0.1的vanilla梯度下降（β= 0），运行50次迭代并观察损失如何衰减。

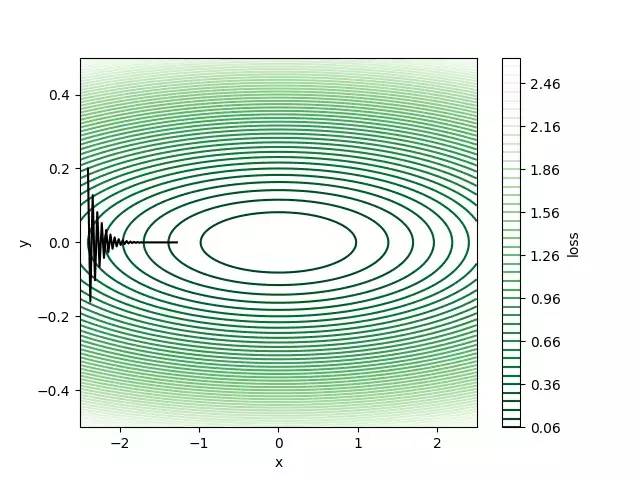
50次迭代后损失大约为0.1，但仍然远离全局最小值（0,0），其中损失为零。 我们可以看到梯度保持改变方向，因为y方向上的梯度正在改变每次迭代的符号，这使得算法缓慢地逼近最佳结果。 我们可以增加动量来加快学习速度。 让我们尝试β= 0.8并运行相同数量的迭代进行权重更新。

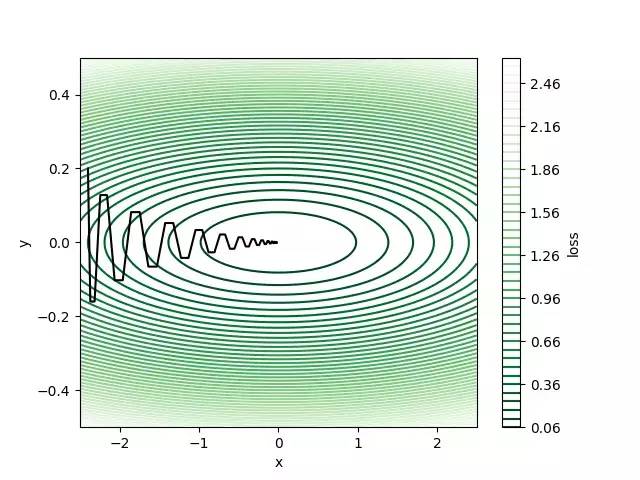
我们现在使用动量实现相同迭代次数，最终损失为2.8e-5！ 因为x方向上的梯度总是指向正x方向，所以可以累积速度。 实际上，这意味着在x方向上具有更大的学习速率，因此与香草梯度下降相比，它可以达到相同迭代次数的更低损失。 这也是为什么动量可以抑制振荡的原因。

我们可能想知道如果我们选择β= 0.9，它会不会更多地积累速度并更快地达到全局最小值？

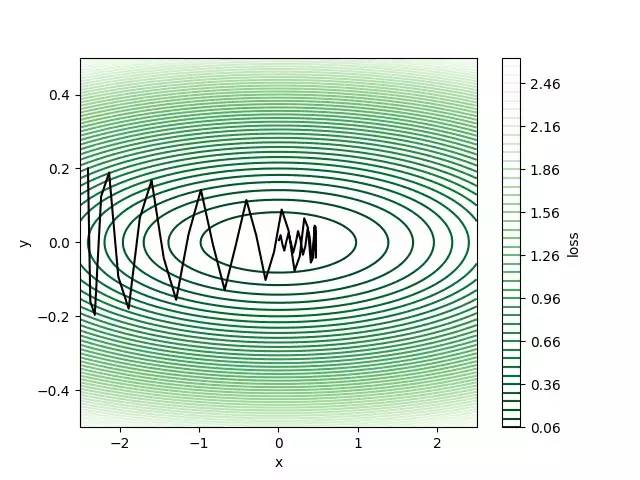
答案是不。 上图显示，过大的速度将通过大步长的全局最小值。 我们还可以绘制速度 - 迭代关系，以分别表示速度如何在x和y方向上变化。

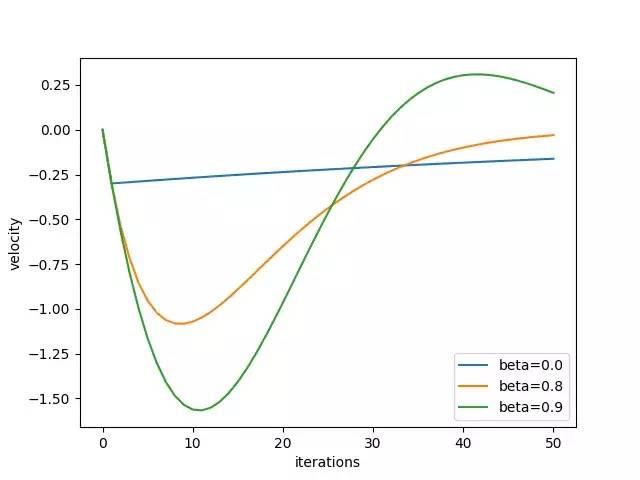
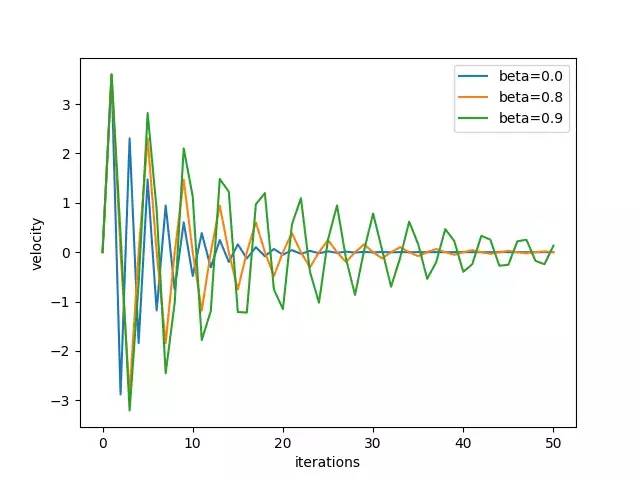
结论

我们直观地表明，当损失表面像乌鸦一样时，具有动量的梯度下降比香草梯度下降更快收敛。 我们还明白到β不能太大，因为它会积累太多的动量并快速超过最佳点。

原文链接：

https://medium.com/@hengluchang/visualizing-gradient-descent-with-momentum-in-python-7ef904c8a847

-END-

专 · 知

人工智能领域26个主题知识资料全集获取与加入专知人工智能服务群: 欢迎微信扫一扫加入专知人工智能知识星球群，获取专业知识教程视频资料和与专家交流咨询！

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请加专知小助手微信（扫一扫如下二维码添加），加入专知主题群（请备注主题类型：AI、NLP、CV、 KG等）交流~

 AI 项目技术 & 商务合作：bd@zhuanzhi.ai, 或扫描上面二维码联系！

请关注专知公众号，获取人工智能的专业知识！

点击“阅读原文”，使用专知