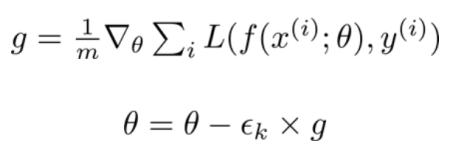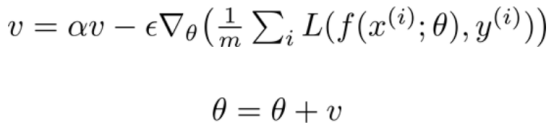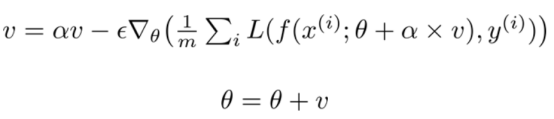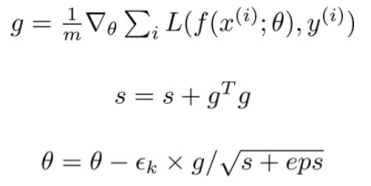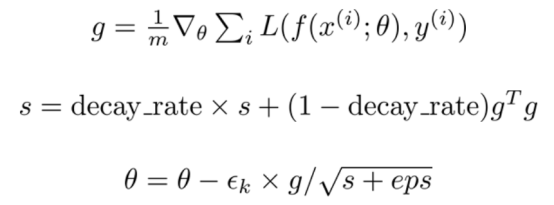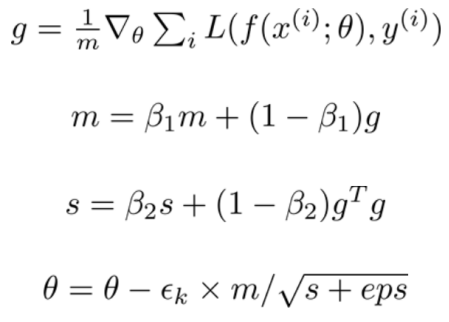【干货】深度学习需要了解的四种神经网络优化算法- 专知

【干货】深度学习需要了解的四种神经网络优化算法

【导读】近日，Vadim Smolyakov发表了一篇博客，针对当前神经网络的优化算法进行了总结，并利用简单的CNN网络在NMIST数据集上进行实验，探讨不同的优化方法的效果好坏。其中考虑了四种神经网络训练的优化方法：SGD，Nesterov Momentum，RMSProp和Adam，并用TensorFlow进行训练。作者最终得出结果：使用Nesterov Momentum和Adam的SGD产生的结果更好。如果您对神经网络的优化算法还不是很了解，那么相信这篇文章将会给您很好的启发！专知内容组编辑整理。

Neural Network Optimization Algorithms

——A comparison study based on TensorFlow

神经网络优化算法

训练神经网络的最流行的优化算法有哪些?怎么进行比较?

本文在MNIST数据集用卷积神经网络（CNN）进行实验，来回答上述优化问题。

▌随机梯度下降（SGD）

SGD通过数据的一个大小为（m）的子集（subset）或一个小批量（mini-batch）来从梯度负方向上更新模型参数（theta）：

神经网络由 f(x(i); theta)表示，其中x（i）是训练数据，y（i）是标签，损失函数L的梯度是根据模型参数θ计算的。学习率（eps_k）决定了算法沿着梯度（在最小化的情况下为负方向，在最大化的情况下为正方向）下降的步长大小。

学习率是非常重要的超参数。学习率太高（例如> 0.1）会导致参数的更新错过最佳值，学习率太低（例如<1e-5）将导致过长训练时间。一个好的策略是学习率初始化为1e-3，并使用学习率调度器来降低学习率（例如，每四个时间段（epoch）将学习速率减半的一个步长调度器）：

def step_decay(epoch):
    lr_init = 0.001
    drop = 0.5
    epochs_drop = 4.0
    lr_new = lr_init * \
             math.pow(drop, math.floor((1+epoch)/epochs_drop))
    return lr_new

一般来说，我们希望学习率（eps_k）满足Robbins-Monroe条件：

第一个条件确保算法不论起点如何，都能够找到一个局部最优解，第二个是控制振荡。

▌动量（Momentum）

动量累积以指数方式进行衰减，补偿按照过去梯度的均值进行移动:

因此，步长取决于梯度序列的大小和排列的顺序，动量参数alpha的通常值设为0.5和0.9。

▌涅斯捷罗夫动量（Nesterov Momentum）

涅斯捷罗夫动量（Nesterov Momentum）受涅斯捷罗夫加速梯度法的启发：

涅斯捷罗夫动量和标准动量之间的区别在于对梯度进行评估，涅斯捷罗夫动量是在应用了当前速率后对梯度进行评估，因此涅斯捷罗夫的动量为梯度增加了一个校正因子。

▌AdaGrad

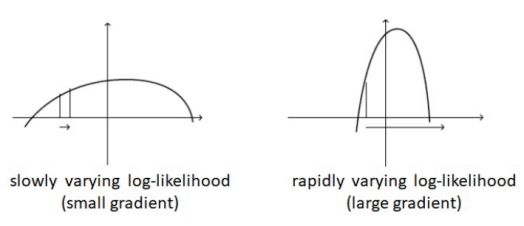
AdaGrad是一种设置学习率的自适应方法[3]。我们考虑下图中的两种情况：

左图：缓慢变化的对数似然（小梯度）右图：快速变化的对数似然（大梯度）在目标缓慢变化（左图）的情况下，梯度通常（在大多数点）进行小幅度变化。因此，我们需要一个大的学习速率才能快速达到最优解。在目标快速变化（右图）的情况下，梯度通常是非常大的。使用大的学习速率会导致非常大的步长，来回振荡，但无法达到最优值。

出现这两种情况的原因是学习率的设置与梯度无关。AdaGrad通过积累到目前为止所有的梯度的平方，并将学习率除以这个总和的平方根来解决这个问题：

因此，获得高梯度的参数将会降低其有效学习率，而接收小梯度的参数将增加其学习率。在更平缓的斜率方向上，以及在大学习率的情况下，更谨慎的更新会带来更大的进步。

▌RMSProp

RMSProp改进了AdaGrad的方法，将梯度的累积变成指数加权的移动平均值，即不考虑距离很远的梯度值[4]：

注意，AdaGrad表示，即使在训练开始阶段累积的梯度而导致梯度保持不变，其学习率也会降低。通过引入指数加权移动平均值，离得更近的历史梯度值相对于离得远的历史值被赋予更大的权重。因此，RMSProp已被证明是一种有效的、实用的深度神经网络优化算法。

▌Adam

Adam从“自适应时刻”衍生而来，它可以被看作是RMSProp和动量组合的一个变体，它的更新看起来像RMSProp（除了使用平滑版本的梯度来代替原始随机梯度），Adam的更新还包括一个偏差修正机制[5]：

建议的值是beta_1 = 0.9，beta_2 = 0.999，eps = 1e-8。

▌实验

我使用四种不同的优化器：SGD，Nesterov Momentum，RMSProp和Adam，并用TensorFlow以1e-3的学习速率和交叉熵损失在MNIST数据集上训练CNN网络。下图显示了这四种优化器的训练损失值与迭代值：

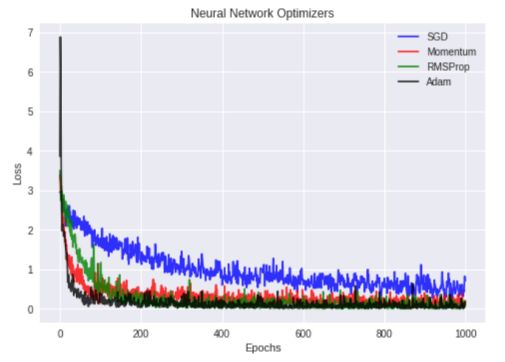
从上图中我们可以看出，Adam和Nesterov Momentum优化器产生的训练损失最低！

▌代码

所有的代码链接：

https://github.com/vsmolyakov/experiments_with_python/blob/master/chp03/tensorflow_optimizers.ipynb

▌总结：

我们在训练神经网络的过程中比较了使用不同优化器的效果，并对它们的工作原理有了直观地认识。我们发现，用TensorFlow在MNIST数据集上训练简单CNN时，使用Nesterov Momentum和Adam的SGD产生的结果最好。

▌References

[1] Ian Goodfellow et. al., “Deep Learning”, MIT Press, 2016

[2] Andrej Karpathy, http://cs231n.github.io/neural-networks-3/

[3] Duchi, J. ,Hazan, E. and Singer, Y. “Adaptive subgradient methods for online learning and stochastic optimization”, JMLR, 2011.

[4] Tieleman, T. and Hinton, G. “Lecture 6.5 — RMSProp, COURSERA: Neural Networks for Machine Learning”, Technical Report, 2012.

[5] Diederik Kingma and Jimmy Ba, “Adam: A Method for Stochastic Optimization”, ICLR, 2015

原文链接：

https://towardsdatascience.com/neural-network-optimization-algorithms-1a44c282f61d

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

同时欢迎各位用户进行专知投稿，详情请点击：

【诚邀】专知诚挚邀请各位专业者加入AI创作者计划！了解使用专知！

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！

点击“阅读原文”，使用专知！

展开全文

阅读 0+

评论 0+