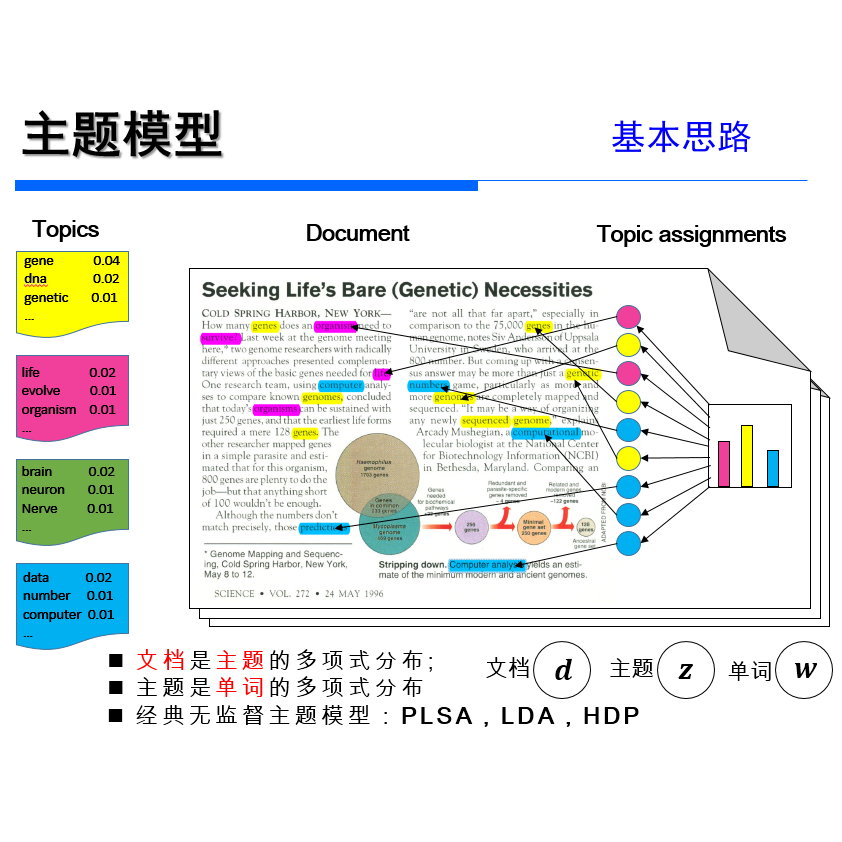
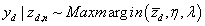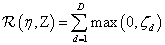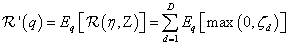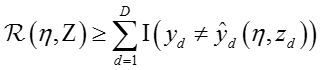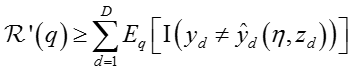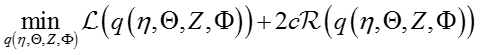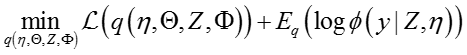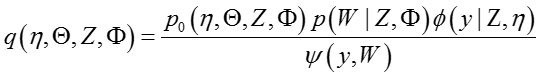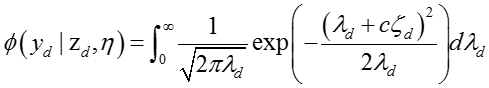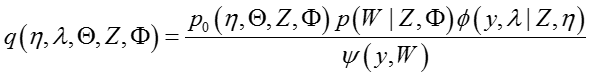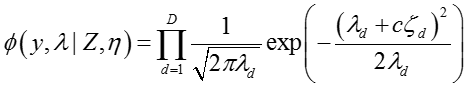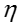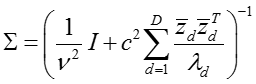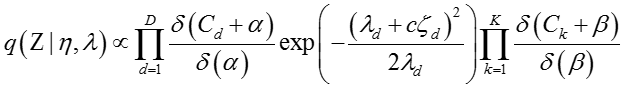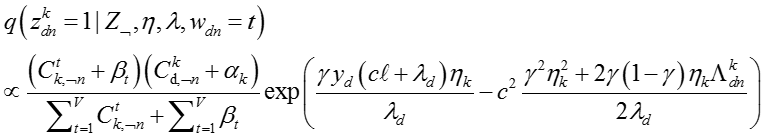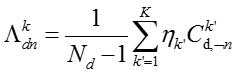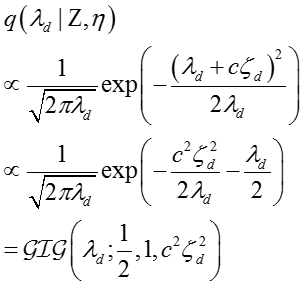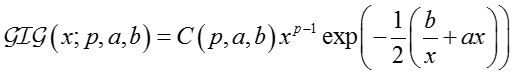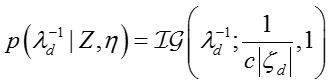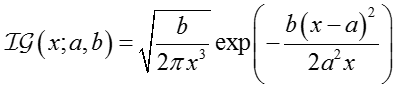2、最大间隔主题模型(Max-margin LDA)
2、最大间隔主题模型(Max-margin LDA)
清华大学朱军老师长时间研究主题模型,其文章“Gibbs Max-margin Topic Models with Data Augmentation”中详细介绍了将Max-margin分类器融入LDA主题模型,并且使用Gibbs sampling的方法给出详细的推导过程,基于此的主题模型在文本分类任务中取得了非常不错的效果。
Maxmargin分类器
Hinge loss是一种目标函数(或者说损失函数)的名称,有的时候又叫做max-margin objective(下面统称为Maxmargin)。其最著名的应用是作为SVM的目标函数。其二分类情况下,公式如下:
其中,y是预测值(-1到1之间),t为目标值(±1)。其含义为,y的值在-1到1之间就可以了,并不鼓励|y|>1,即并不鼓励分类器过度自信,让某个可以正确分类的样本距离分割线的距离超过1并不会有任何奖励。从而使得分类器可以更专注整体的分类误差。
Max-margin LDA
通过Softmax考虑文档的类别标签在上面的SLDA中介绍过了,但是如何利用类似于SVM分类思想的Maxmargin分类器考虑文档的类别标签,并融入LDA构建一个完整的有监督主题模型,由于最大间隔约束的特殊性,其求解有好多方式,本文主要介绍其Gibbs Sampling方法。其文章“Gibbs Max-margin Topic Models with Data Augmentation”做了详细的公式推导和分析,下面简要介绍一下内容主要摘自该论文。
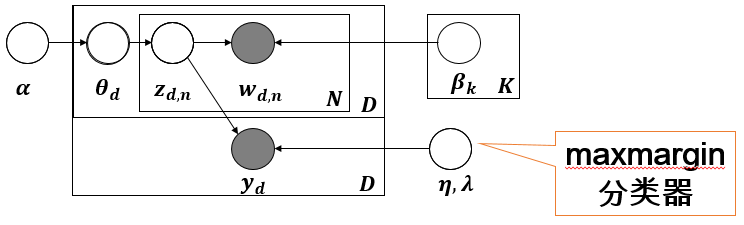
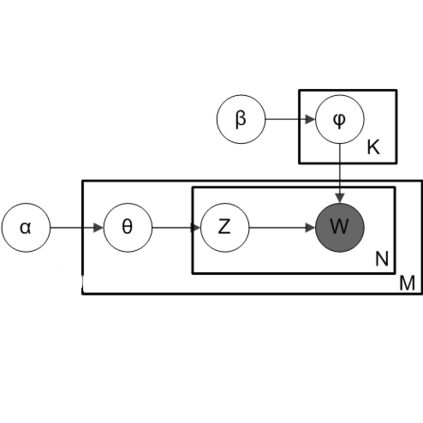
首先主题模型的图模型生成过程如下图,与SLDA并没有什么区别,其生成过程可参照:
-
对于每一个主题k:
-
从Dirichlet分布中获取文档-主题分布 ;
-
对于每个单词 :
-
首先从文档-主题分布中获取一个主题: ;
-
然后从对应的主题以及主题-词分布中获取一个词:
-
获取单词类别标签:
作者在考虑类别信息的时候采用Maxmargin分类器,即:
如何融合Maxmargin分类器,如何学习Expected Margin Loss,推导过程如下:
设符号 表示文档-主题分布; 表示分类器模型。如果我们已经从后验分布中获取了文档-主题分布和预测模型,我们就可以定义线性判别函数如下:
然后加入符号规则(sign)就可以预测类别了:
利用hinge loss损失函数的公式,设 ,其中 是代价参数(SVM中也称为间隔,即Margin),则损失(hinge loss)函数为:
期望损失(expected hinge loss)为:
由于训练文档总是有限的,因此上述期望损失是Maxmargin分类器训练错误(training 误差)的上界,即:
有,
其中,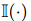
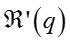
根据原始数据的margin约束规则,优化目标变为:
其中c是正则化参数。
利用collapsed Gibbs sampling algorithm求解模型参数,令
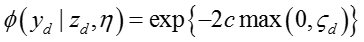
其中
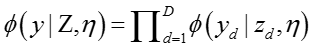
归一化后验分布为:
其中,
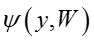
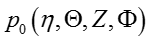
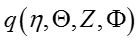
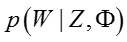
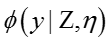
由于Maxmargin分类器并不像Softmax分类器那样方便写出分类的概率形式,所以一直难以应用到LDA主题模型中,幸好:
Specifically, using the ideas of data augmentation (Tanner and Wong, 1987;
Polson and Scott, 2011), we have Lemma 2
上述研究得出一个重要的结论:
所以,后验联合概率分布可以写成:
其中:
这样,就可以利用Gibbs
Sampling方法采样不同的未知变量,在分别采样三个未知变量
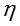
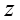
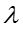
For :
常用isotropic Gaussian
distribution分布作为
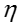
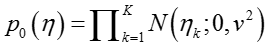
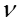
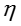
即服从K维的高斯分布(K-dimensional Gaussian
distribution)。其后验均值和后验协方差为
,
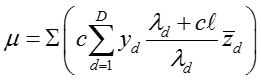
所以,可以很轻易的从多项高斯分布(multivariate Gaussian
distribution)中采样一个样本,协方差转置可以用乔里斯基矩阵分解(Cholesky
decomposition)获取。
For :
给定其他变量,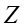
其中: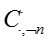
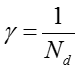
For :
参数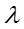
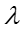
其中
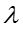
distribution),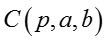
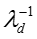
distribution)
其中:
还没完成 后续完善中
参考文献
- MaxmarginLDA—Zhu J, Chen N, Perkins H, et al. Gibbs max-margin topic models with data augmentation[J]. Journal of Machine Learning Research, 2013, 15(1):1073-1110.