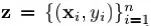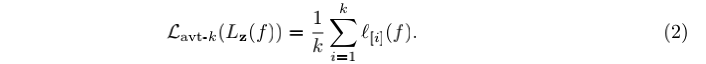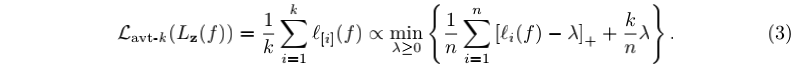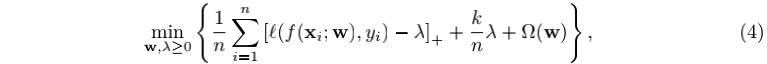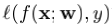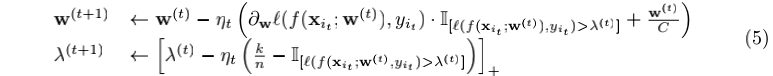【论文分享】中科院自动化所多媒体计算与图形学团队NIPS 2017论文提出平均Top-K损失函数,专注于解决复杂样本
点击上方“专知”关注获取专业AI知识!
【导读】损失函数的设计一直是机器学习和模式识别中的核心问题。目前中国科学院自动化研究所和美国纽约州立大学奥尔巴尼分校合作提出了一种新的聚合损失函数,即平均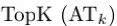
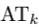
论文:Learning with Average Top-k Loss
▌1. 引言:
很多机器学习任务目标于学习一个映射函数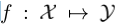
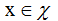
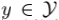
记f在样本(x, y)上损失为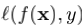
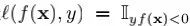
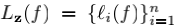
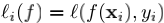
我们称L为聚聚聚合合合损损损失失失(aggregate loss),即把每一个样本的单个损失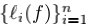
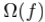
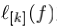
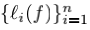
Figure 1: 在二分类任务中,不同的聚合损失在仿真数据上的性能比较。Bayes最优分类边界在图中以阴影显示,其中单个样本的损失采用logistic损失。第2列和第4列的图显示了每种情况下当k变化时,ATk损失对应错分比例。
图1结合仿真数据显示了最小化平均损失和最小化最大损失分别得到的分类结果。可以看出,当数据分布不均衡或是某类数据存在典型分布和非典型分布的时候,最小化平均损失会忽略小类分布的数据而得到次优的结果;而最大损失对样本噪音和外点(outliers)非常的敏感,即使数据中仅存在一个外点也可能导致模型学到非常糟糕的分类边界;相比于最大损失损失,第k大损失对噪音更加鲁棒,但其在k > 1时非凸非连续,优化非常困难。
由于真实数据集非常复杂,可能存在多分布性、不平衡性以及噪音等等,为了更好的拟合数据的不同分布,我们提出了平均Top-K损失作为一种新的聚合损失。
▌2. 学习平均Top-K损失
2.1 平均Top-K损失定义
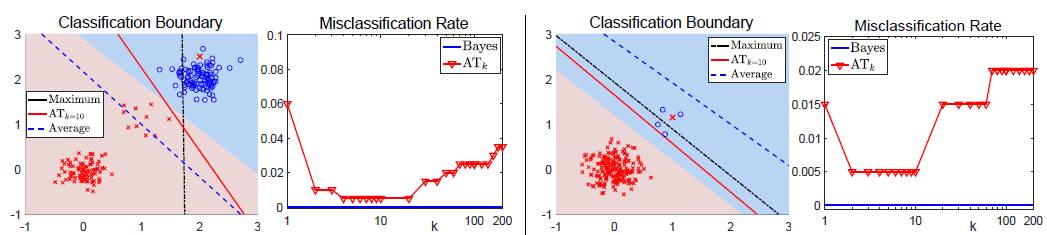
平均Top-K(Average Top-K Loss, ATk)损失定义为样本集z上的前k个最大的损失的平均值,即
可以看出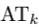
损失包含了平均损失(k = n)和最大损失(k = 1)。
损失是第k大损失的凸上界。
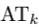
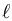
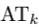
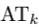
2.2
损失的分析和优化
受限于排序算子(前k个最大的损失的平均),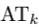
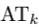
Lemma 1 (Lemma 1, W. Ogryczak et al. 2003).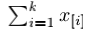

其中
根据引理1,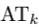
可以看出,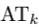
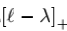
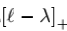
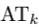
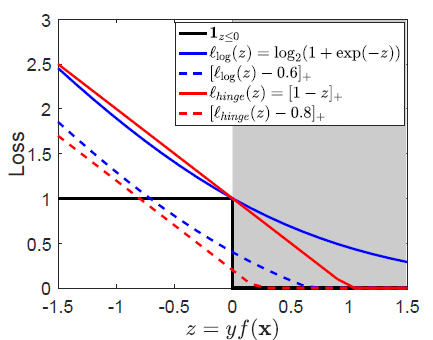
Figure 2: ATk损失在单个损失上的释义,阴影部分对应正确分类的样本。
以二分类问题为例,由于0-1损失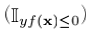
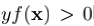
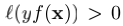
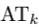
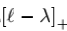
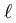
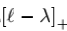
以图1中的不平衡数据为例,由于正类样本很多,当采取平均聚合损失时学习到的分类器会将所有负类样本都错分成正类以达到整体损失最小。而当我们采取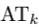
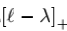
模型优化: 利用公式(3),不失一般性,我们假定f是一个由参数w刻画的的学习模型,最小化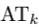
其中Ω(w)为作用到模型参数w上的正则项。容易看出当
和Ω(w)是关于w的凸函数的时候,公式(4)中的目标函数是关于(w, λ)的联合凸函数。因此我们可以采用随机(次)梯度法来方便的优化模型(4),特别的,当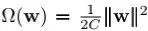
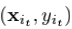
其中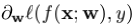
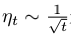
2.3 实验分析
我们在分类问题和回归问题中对ATk损失进行实验分析,在实验中我们采用线性预测函数,即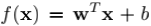
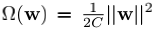
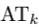
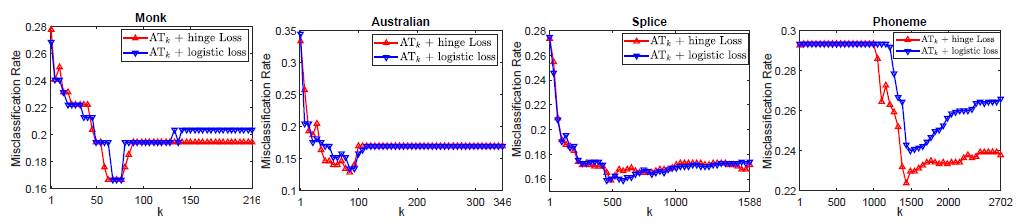
Figure 3: 分类错误率w.r.t. k
图3给出了在二分类实验中,在四个数据集上分类错误率随k的变化的变化曲线,其中单个样本的损失分别为logistic损失和hinge损失。可以看出在这些数据集上当k = 1时,数据中潜在的噪音对分类结果有很大的负面影响,分类结果比较差;随着k的逐渐增加,噪音和外点数据对分类器的影响逐渐被削弱,分类性能逐渐变好;当k持续增加时(如k = n),由于大量容易被分类的样本被逐渐增加进来,这些简单样本上的非0损失会对分类器带来负面的影响,分类性能反而下降。
更多的理论分析和数值实验结果,请参见原文。
▌3.总结
在该工作中,我们分析了平均损失和最大损失等聚合损失的优缺点,并提出了平均Top-K损失(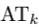
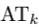
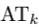
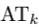
论文链接:
http://papers.nips.cc/paper/6653-learning-with-average-top-k-loss
▌特别提示-Learning with Average Top-k Loss论文下载:
请关注专知公众号(扫一扫最下面专知二维码,或者点击上方蓝色专知),
后台回复“LATK” 就可以获取论文pdf下载链接~
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域24个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请扫一扫如下二维码关注我们的公众号,获取人工智能的专业知识!
请加专知小助手微信(Rancho_Fang),加入专知主题人工智能群交流!
点击“阅读原文”,使用专知!