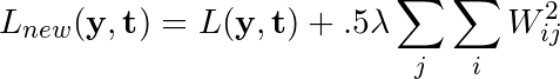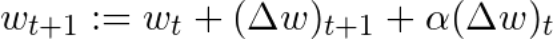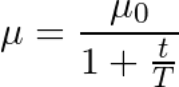【干货】加速梯度下降的若干小技巧- 专知

【干货】加速梯度下降的若干小技巧

【导读】在训练神经网络的时候，使用标准梯度下降法常常使网络陷入局部最小值，从而造成实验结果不佳。本文介绍了几种标准梯度下降的基础的改进算法。如批量梯度下降，正则，动量，变化学习率等。这些改进算法较为基础，但是正确地使用能帮助你成功地训练模型。另外，文末还列举了几种最新的、高效的改进算法：Adam，Adagrad和Adadelta，感兴趣的读者可以详细了解一下。

Improving Vanilla Gradient Descent

Performance improvements applied to training neural networks

▌简介

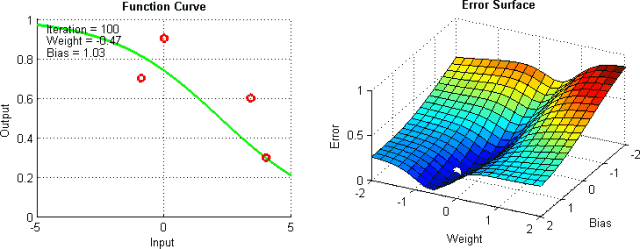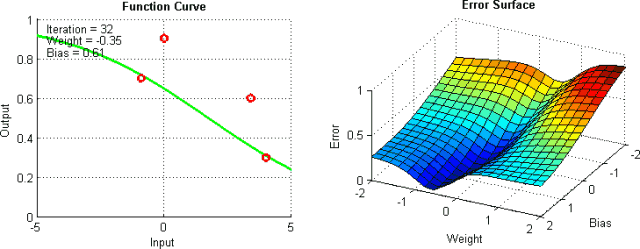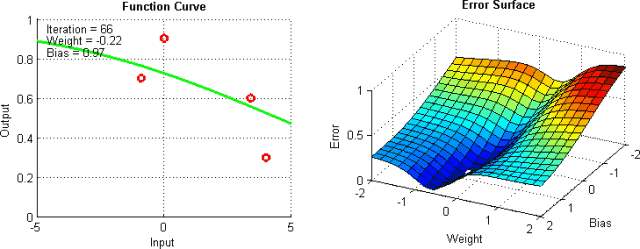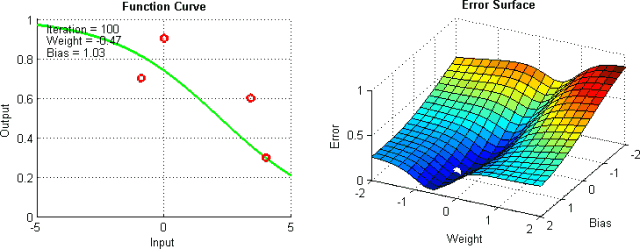
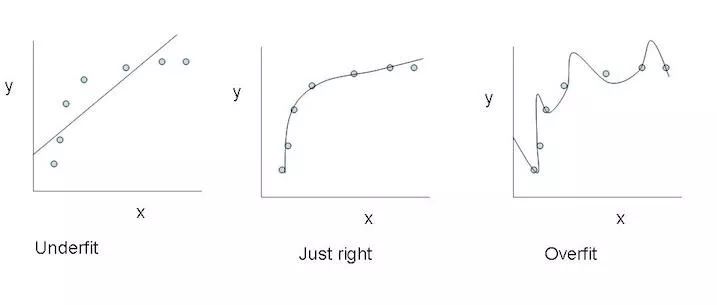
当我们用梯度下降训练神经网络时，我们是冒着网络有可能有陷入局部最小的风险的情况。这是因为误差曲面本身并不是凸的，因此曲面可能包含许多独立于全局最小值的局部最小值。另外，即使网络达到了全局最小值并收敛到训练数据的理想点，也不能保证我们的模型有很好的泛化性能。因为模型很容易过拟合。

尽管没有办法防止过拟合发生，我们仍然可以找到几种方法来缓解它。

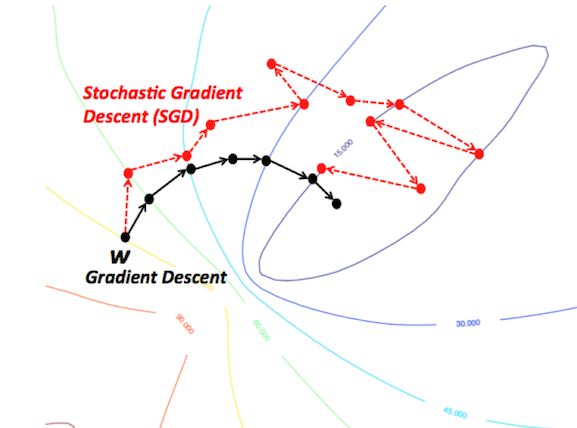
▌随机和小批量随机梯度下降

标准梯度下降算法每次迭代更新的是训练数据的子集。 SGD将使用每个样本更新一次权重，而mini-batch SGD将使用预定义的数字（通常远小于训练样本的总数）。这允许更快地训练，因为它需要更少的计算，因为我们在每次迭代中都不使用整个数据集。它也可能带来更好的表现，因为网络在训练过程中的随机性使得优化过程能够更好地规避局部最小值，并且只使用小部分数据集有助于防止过拟合。

▌正则

一般而言，正则通过向损失函数添加一个表示模型复杂度的值, 来惩罚模型的复杂性. 在神经网络的情况下，它惩罚较大的权重，因为这可能表明网络对该权重对应的训练数据过拟合。

使用L2正则化，我们可以重写损失函数，将网络的原始损失函数表示为L（y，t），正则化常数表示为λ：

正则化将网络中每个权重的平方和添加到损失函数中，惩罚那些给每一个连接赋予过多的权重的模型，来减少过拟合。

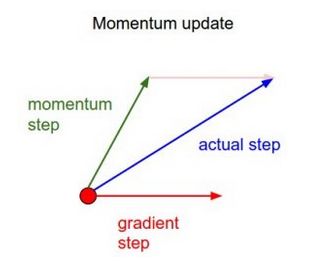
▌动量

动量，简单地说，将过去权重更新量的一小部分增加到当前的权重更新。这有助于防止模型陷入局部最小值，即使当前的梯度为0，上一个梯度很可能不是，所以它很容易卡住。通过使用动量，沿着误差表面的运动总体上也更加平滑，并且网络可以在整个运动中更快地移动。

用简单的动量，我们可以将重量更新方程改写如下，表示α作为动量因子：

还有其他更先进的动量形式，如涅斯捷罗夫方法（Nesterov method）。

▌学习率变化

我们可能会退化学习速度，并随着时间的推移而下降，而不是在整个训练中使用恒定的学习速度。

最常见的学习率变化具有如下的1 / t关系，其中T和μ_0是超参数，并且μ是当前学习速率：

这通常被称为“先搜索后收敛”模式，直到t到达T，网络处于“搜索”阶段并且学习速率没有太大下降，此后，学习速率减慢并且网络达到“收敛阶段。一开始我们优先探索搜索空间并拓展我们对空间的总体知识，随着时间的推移，我们转而利用我们已经找到的搜索领域中的优势领域并将其缩小到特定的最小值。

▌结论

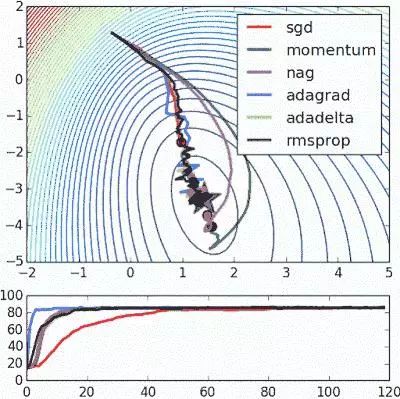
以上只是改进标准梯度下降算法的部分方法。当然，这些方法中的每一种都会为模型添加超参数，从而增加调整网络所花费的时间。最近，Adam，Adagrad和Adadelta等新算法出现了，它们使用了部分上述技术以及其他新的技术。他们倾向于根据每个参数进行优化，而不是全局优化，因此他们可以根据个人情况微调学习率。他们在实践中往往更快更好地工作;然而，要正确实施它们要困难得多。下面的图表说明了每个提到的梯度下降变化同时工作。观察到更复杂的版本比简单的动力或SGD版本更快地收敛。