【导读】香农1948年发表的论文“通信的数学理论”不仅奠定了现代信息论的基础,他直接将通信工程问题抽象为数学理论问题的方法论特别值得学习。这实例充分说明智能本质的揭示或对大脑的深度认知最后是依赖数学层面上的描述。

信息论中最为基本的概念就是香农熵
(第8页),由此可以导出信息论中其它各种定义,以至我们常规应用的其它经验式定义(以后会提到)。学习信息论基础知识时要避免仅是概念与定义的简单记忆,要尽量结合个人研究领域中的问题进行思考,并给出个人理解(如第20页中监督学习中的解释与思考)。这样有益于未来更快地发展创新工作。还要明白信息论理论仍在发展中,包括各种熵定义的不断出现。我们在第28页中示例了传统互信息定义在机器学习应用中的问题。可能这类问题在通讯领域的传统应用中不存在。为更好理解内容,建议读者对其中每个例题自行计算一下。你一定会有新的理解。对于有些内容现在无法理解(如第20页),不要着急。可以随着以后课程学习后,回头复习来不断理解。抱歉该课程未有提供视频或更多中文解说。基于本课件自学能够逐步理解也是能力的培养,从事科研工作必须要过这个关。建议有关作业尝试用笔记录回答一下,有益于反复思考。
此课件后面附加一个文件。
是英国对口相声“热力学第一和第二定律”说明。
https://www.xiami.com/song/1794511373
1. 针对香农抓住了通信工程中的本质问题,请总结你从语义表达与计算表达中给出的理解。
2. 结合第28页中示例,以定理方式证明互信息可能存在的问题。
3. 你认为怎样应对互信息中这个问题,并给出具体解决方案。
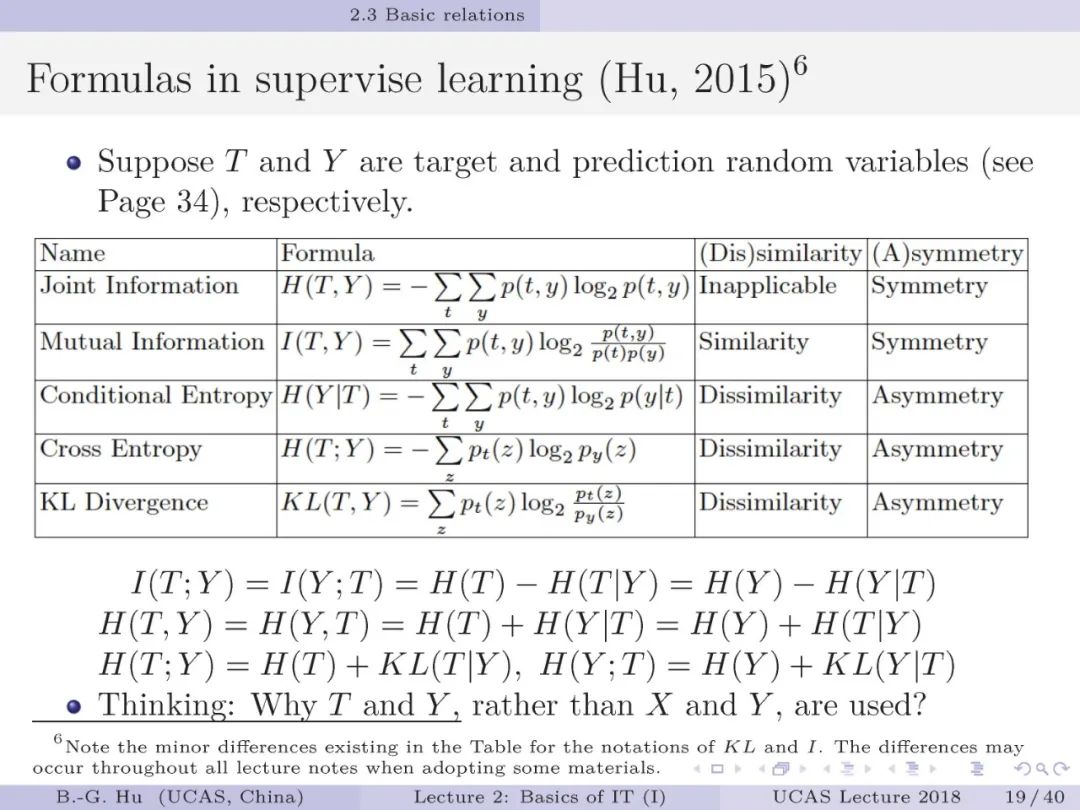
第19页: 机器学习中通常会将互信息作为“相似性”度量,条件熵、散度、交叉熵作为“误差或损失”指标来应用。
统称它们为指标或准则是可以包容散度这样非度量类别。
但是要理解这些信息指标是关于两个随机变量之间独立性的测量(第22页)。
本质上不是相似性或损失的测量。
第20页: 这页内容对于理解信息论指标在监督学习中的内涵十分重要。
其中T是目标类标变量,Y是预测类标变量。
举例一下,T中100个样本,有50个苹果,有50个鸭梨为标签。
因此H(T)是固定的。
而分类学习中,我们可能预测为30个苹果,70个鸭梨。
思考问题中,所谓“不正确(incorrect)”是由于应用了H(Y)为目标基点(Baseline),该基点犹如移动目标。
从理论上讲,移动目标或固定目标对优化问题解应是一致的。
从实际优化搜索而言,移动目标更易引起搜索中的震荡现象。
因此认为是“不正确”。
我们对互信息在在监督学习中的语义内涵给出了不同解释样例。
在实际应用中,这种解释性特别重要,要兼有语义与计算层面的解释理解。
比如思考问题中提到了聚类问题,这些指标的物理意义与选择方面解释是值得思考的问题。
要理解机器学习中首要问题“学习目标选择”值得更多重视。
对理论上等价的指标,选择某个的原因是什么呢?
对各种学习目标我们有必要开展“系统化设计方法”研究(2001年我们在《自动化学报》关于模糊系统综述文章中对“系统化设计方法”给予了讨论)。
当信息论指标得到更多应用时,我们需要准确理解。
比如许多分类学习方法中将交叉熵以误差或损失方式来说明。
但是,此图及第19页计算公式告诉我们交叉熵H(T;Y)最小值应是H(T)且应大于“零”值。
因为H(T)=0意味全部样本为一类。
交叉熵大于“零”的性质说明与误差概念显然不同。
我个人理解交叉熵可以有“零”值解是借用了交叉熵计算公式,且该公式应该称为逻辑损失(Logistic Loss)而非交叉熵。
常规术语应用中要理解这之间的差异。
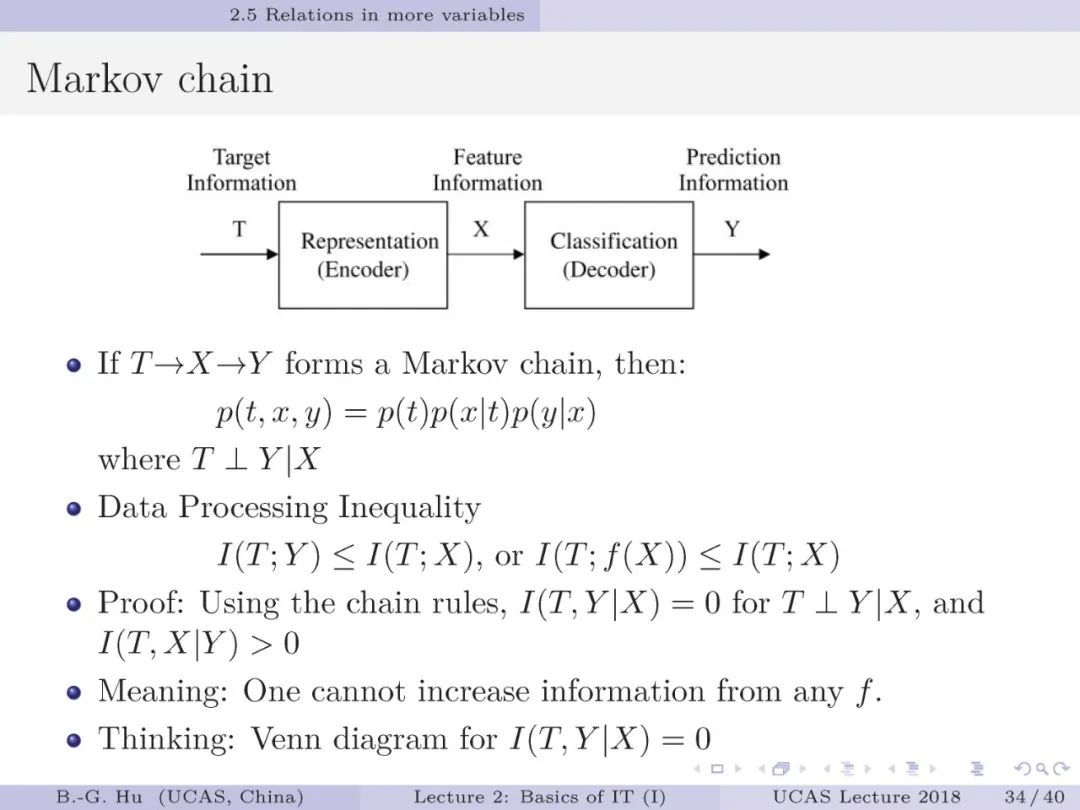
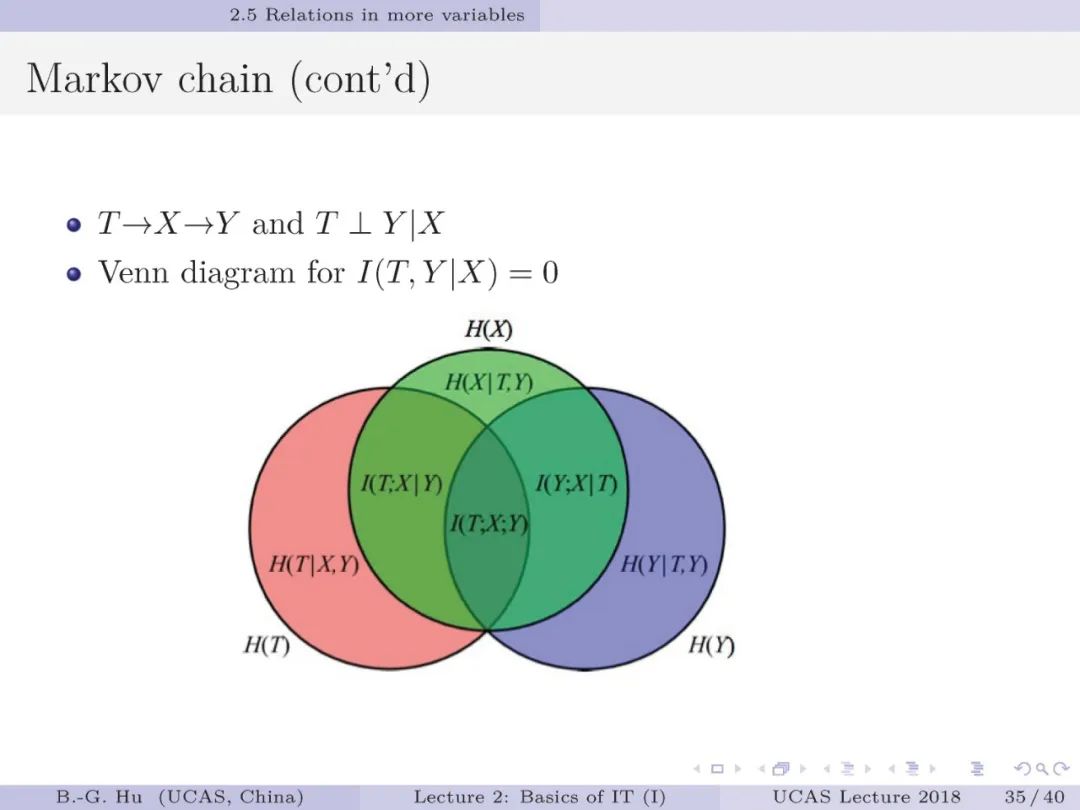
第23-28页: 二进制信道是通讯中最为基本的结构。
在监督学习中这犹如对应了二值分类器。
其中“擦除”功能(第24页)将增加一维输出,对应二值分类器就是增加了一个拒识(或未知)类别输出。
第26页中的GBC结构可以描述其它结构。
从机器学习角度讲,GBC可以称为带拒识类别二值分类器。
通讯理论中通常应用“条件概率分布”描述二进制信道,这里我们应用“联合概率分布”来描述,不仅可以导出“条件概率分布”,而且可以对应二值分类器中的混淆矩阵。




































英国对口相声“热力学第一和第二定律”说明




专知便捷查看
便捷下载,请关注专知公众号(点击上方蓝色专知关注)

专知,专业可信的人工智能知识分发,让认知协作更快更好!欢迎注册登录专知www.zhuanzhi.ai,获取5000+AI主题干货知识资料!

















































