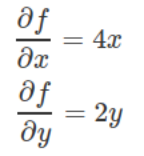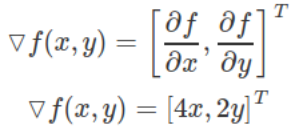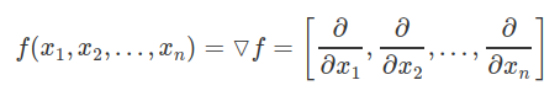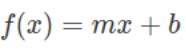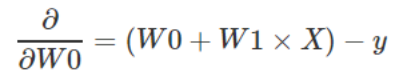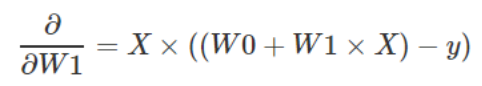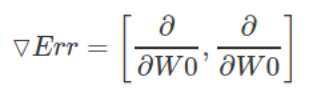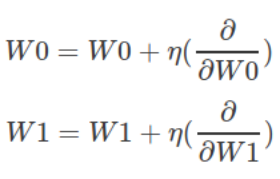【干货】一种直观的方法认识梯度下降- 专知

【干货】一种直观的方法认识梯度下降

【导读】本文是深度学习专家Thalles Silva分享的一篇技术博客，主要讲解机器学习算法中的梯度下降。首先从形象的角度介绍梯度下降：梯度、偏导数等。然后，根据一个具体的例子“根据历史数据来预测当前房价”讲解梯度下降及其代码实现，在实例中主要使用Mini-Batch梯度下降（Mini-Batch Stochastic Gradient），并解释了其误差迭代曲线的变化趋势和和原因，不太了解梯度下降算法的读者可以仔细阅读下。

作者博客：

https://sthalles.github.io/

An Intuitive Introduction to Gradient Descent

毫无疑问，梯度下降是大多数机器学习（ML）算法的核心和灵魂。我认为你应该花时间去理解它。因为一旦你理解了它，你会更好地理解大多数ML算法的工作原理。

为了学习梯度下降的核心，我们在文中举了一个例子，这个任务是这个领域的老问题了，即通过历史数据作为先验知识来预测房价。

▌基本概念

假设你想爬上一座高山。你的目标是以最快的速度登上山顶。你环顾四周，你意识到你有多条路径可以开始。由于你处于最底层，所有这些选项似乎都可以让你更接近顶峰。

但是你想以最快的方式达到顶峰。那么，怎么做呢？

到目前为止，如果你还不清楚如何采取这一步骤，你可以使用梯度来帮助你。

正如Khan Academy 视频中所述，梯度捕捉了一个多变量函数的所有偏导数。

让我们一步一步看看它是如何工作的。

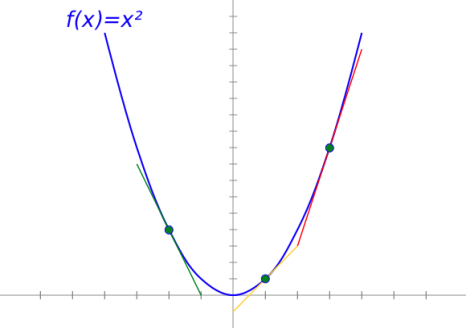
简单来说，导数就是某个点的函数变化率或斜率。

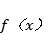
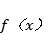
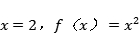
以函数为例。的导数是计算给定点x处斜率的另一函数f'（x）。在这种情况下，对于的斜率是2x或2 * 2 = 4。

简而言之，导数指向最陡峭的上升方向。梯度是和导数完全一样的东西。 唯一的例外是：梯度(Gradient )是存储偏导数的矢量值函数。 换句话说，梯度是一个向量，它的每个分量都是相对于一个特定变量的偏导数。

作为另一个例子，取函数。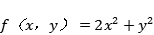

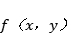
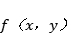
这里，是一个多变量函数。它的梯度是一个矢量，包含的偏导数。第一个关于x，第二个关于y。

如果我们计算f（x，y）的偏函数，我们可以得到。

所以梯度是以下矢量：

请注意，上面每个部分都表示每个函数变量的最陡上升方向。换句话说，梯度指向函数增加最多的方向。

回到爬山的例子，梯度表示指向到达山峰最快的方向。

同理，如果我们有一个具有4个变量的函数，我们将得到一个具有4个偏导数的梯度向量。通常，n变量函数有n维梯度向量。

然而，对于梯度下降(Gradient descent)，这个含义是我们不是很想使f最大化，而是希望将其最小化。

下面举一个具体的任务，来看一下。

▌预测房价(Predicting House Prices)

我们的问题是根据已有历史数据来预测当前的房价。如果要构建一个机器学习模型，我们通常至少需要3个元素。问题T，性能指标P和经验E，模型将从中数据中学习一种模式用于数据的预测。

我们将使用一个简单的线性回归模型尝试来解决这个问题。这个模型将从经验E中学习，并且在训练之后，它可以泛化应用到未知的数据。

线性模型是一个很好的学习模型。它是许多其他ML算法的基础，如神经网络和支持向量机。

对于这个例子，经验E是HOUSES数据集。 HOUSES数据集包含圣路易斯奥比斯波县及其周边地区最近的房地产列表。

该集合包含781个数据记录，可在下面链接以CSV格式下载。在8维特征中，为了简单起见，我们将只关注其中的两个：大小和价格。对于781个记录中的每一个，以平方英尺为单位的大小将是我们的输入特征，而价格是我们的目标值。

https://wiki.csc.calpoly.edu/datasets/wiki/Houses

此外，为了检查我们的模型是否正确地从经验E（数据）中学习，我们需要一种机制来衡量其性能。为此，我们将平方误差总和（SSE）作为我们的衡量标准。

SSE多年来一直是线性回归的基准度量。但理论上，比如绝对误差一样的任何其他误差衡量方式都可以。 SSE的好处是它比绝对误差对错误的惩罚更大。

现在我们已经把我们的算法形式化表示，让我们深入看一下代码。

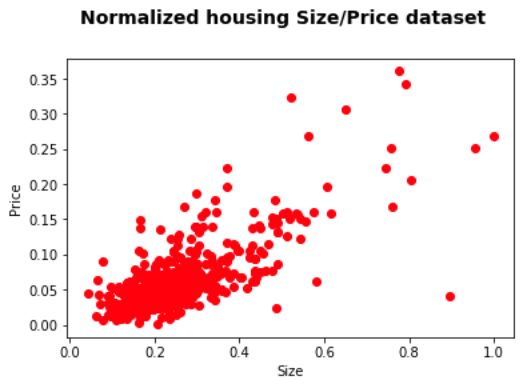
首先我们使用Pandas将数据加载到python中，然后将Size和Prices特征分开。之后，我们对数据进行归一化处理。此外，用归一化数据做梯度下降会比其他情况快得多。

# read the Houses dataset CSV file
housing_data = pd.read_csv("./RealEstate.csv", sep=",")

# only get the Size and the Price features
Xs = housing_data[['Size']]
Ys = housing_data[['Price']]

# get some statistics
max_size = np.max(Xs)
min_size = np.min(Xs)
max_price = np.max(Ys)
min_price = np.min(Ys)

# Normalize the input features
Xs = (Xs - min_size) / (max_size - min_size)
Ys = (Ys - min_price) / (max_price - min_price)

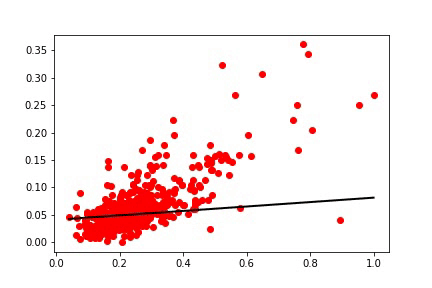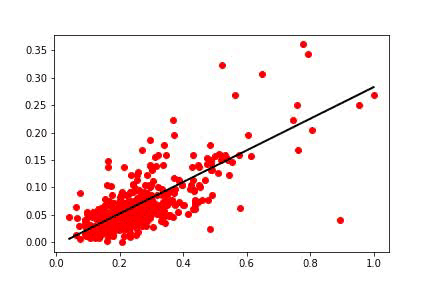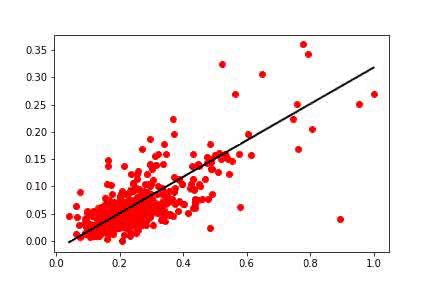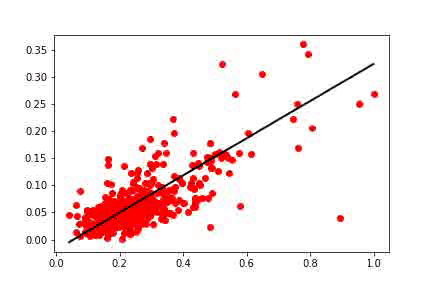
从下图中，你可以看到房屋价格按其平方米的大小分布。

线性回归模型通过在数据上绘制一条直线来拟合数据。因此，我们的模型由一个简单的线性方程表示。

对于线性模型，两个参数是斜率m和偏置b(y轴截距)。我们将要不断改变这两个变量的值来得到最小的误差值，也就是最终的模型参数值。

我们轻微改变两个参数值，使函数值可以沿着误差曲面上最陡的方向下降。每次迭代后，这些权重变化将优化我们的模型，以便模型能更好地表示数据集。

请牢记，对于梯度下降，我们希望采取与梯度相反的方向。

你可以把梯度下降想象成一个在山谷中滚动的球。我们希望它坐在山的最深处（最低点），但是，很容易在其他山谷处。

根据球开始滚动的位置，它可能会停留在山谷的底部。然而不是最低的一个。这被称为局部最小值，在我们的模型中，山谷就是误差面。

请注意，并不是所有的局部最小值都不好。其中一些实际上几乎与最低（全局）一样低（好）。事实上，对于高维误差曲面，最常见的是解决方案找到一个局部最小值，但这个局部最小值不是很差，几乎和全局最优值差不多。

同样，我们初始化模型权重的方式可能导致它停留在局部最小值。为了避免这种情况，我们用来自零均值和低方差的随机正态分布的值初始化两个权向量。

在每次迭代中，我们将从我们的数据集中随机采样子集，并将其与我们的权重线性组合。这个子集称为mini-batch。在线性组合之后，我们将模型预测得到结果送入SSE函数以计算当前误差。

用这个误差值，我们可以计算误差的偏导数以得到梯度。

首先，我们得到关于W0的偏导数。

第二步，同理得到W1的偏导数：

有了这两个偏导数，我们得到了梯度向量：

其中Err是SSE误差函数。

有了这些，下一步就是使用梯度来更新权重向量W0和W1，以最大限度地减少误差值。

我们想要更新权重，以便他们可以在下一次迭代中将误差降低。我们需要使它们沿着每个相应梯度的相反方向。 要做到这一点，我们将在这个方向上采取尺寸为η的小步长。

步长η是学习率，它控制学习的速度。从经验上讲，一个好的学习率值是0.1。最后，更新步骤规则设置为：

在代码中，完整的模型如下所示。注意两个梯度DW0和DW1前面的负号。这保证我们将采取与梯度相反的步骤。

（  DW0 = - (Y_pred-Ys_batch)
    DW1 = - (Xs_batch * (Y_pred - Ys_batch))）
for Xs_batch, Ys_batch in next_batch(Xs, Ys, batch_size=128):

    # linearly combine input and weights
    Y_pred = W0 + np.dot(W1, Xs_batch)

    # calculate the SSE between predicted and true values
    err = 1/2 * sum((Ys_batch-Y_pred)**2)

    # calculate the gradients with respect to W0 and W1
    DW0 = - (Y_pred-Ys_batch)
    DW1 = - (Xs_batch * (Y_pred - Ys_batch))

    # update W0 and W1 in the opposite direction to the gradient
    W0 = W0 + lr * sum(DW0)
    W1 = W1 + lr * sum(DW1)