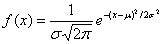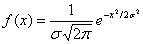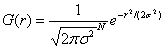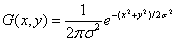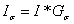【干货】计算机视觉实战系列06——用Python做图像处理
【导读】专知成员Hui上一次为大家介绍主成分分析(PCA)、以及其在图像上的应用,这一次为大家详细讲解SciPy库的使用以及图像高斯模糊实战。
【干货】计算机视觉实战系列01——用Python做图像处理(基本的图像操作和处理)
【干货】计算机视觉实战系列02——用Python做图像处理(Matplotlib基本的图像操作和处理)
【干货】计算机视觉实战系列03——用Python做图像处理(Numpy基本操作和图像灰度变换)
【干货】计算机视觉实战系列04——用Python做图像处理(图像的缩放、均匀操作和直方图均衡化)
SciPy库以及图像高斯模糊实战
SciPy
SciPy是建立在NumPy基础上,用于数值运算的开源工具包。SciPy提供很多高效的操作,可以实现数值积分、优化、统计、信号处理,以及对我们来说最重要的图像处理功能。接下来,本节会介绍SciPy中大量有用的模块。SciPy是一个开源工具包,可以从http://scipy.org/Download下载。
图像模糊
图像的高斯模糊是非常经典的图像卷积的例子。高斯模糊,听起来很高大上,其实就是一种很基础的数学算法应用,不要被“高斯”迷惑了双眼,它并没有高斯本人那么深不可测。高斯模糊是模糊图像的结果.它是一种广泛使用的图形软件的影响,通常会减少图像噪声和减少细节。这个模糊技术的视觉效果是一个平滑的模糊相似,查看图片通过一个半透明的屏幕,从明显不同散景在通常的照明的聚焦透镜或物体的阴影产生的影响。高斯平滑也被用来作为一个预处理阶段计算机视觉算法以提高图像在不同尺度的结构见尺度空间表示和尺度空间的实现。
在数学上,应用高斯模糊图像是一样的卷积一个图像高斯函数。这也被称为一个二维维尔斯特拉斯变换。相比之下,通过循环卷积\能更准确地再现散景功效自傅里叶变换一个高斯是另一个高斯,应用高斯模糊具有降低图像的高频成分的影响;高斯模糊是一个低通滤波器。
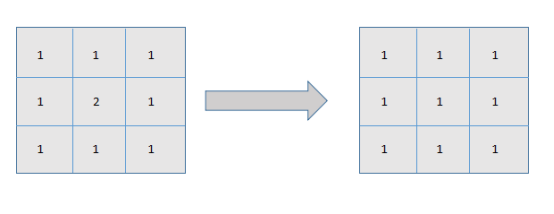
模糊的本质,实际上就是每一个图片中的像素取周边像素的均值.如下图所示:
在上图左边的方框中,我们首先定义一个中心点,即为“2”这个像素点。我们需要对中心点取值进行变换,变换规则为:中心处点的值取附近所有点值的平均值,由图中像素点可得:中心点的像素值就变成了1。在数值上,这种操作可以看成是一种平滑化的操作。那么对于变换后的二维图像来说,便可以看作是有了“模糊”的效果,中心点失去了自己本身的像素值,相当于细节丢失。而图像的模糊程度就完全取决于图像的模糊半径了。从值德角度来说,数值更加的趋向于平滑。
高斯模糊的核心就是取中心点周围所有像素点的均值作为自己的像素值,以此来达到平滑效果,在算法上,涉及到很多问题,从这些问题也是影响高斯模糊速度(模糊效率)的重要方面因素。
那么,影响高斯模糊的速度因素又有什么呢?根据我们分析,由于要对所有的点进行计算,所以高斯模糊是一个相对而言较为耗时的作用,而模糊所需的时间取决点也有很多,诸如算法,以及图片自身属性以及人的要求,机器性能都是影响到高斯模糊时间。
其中对高斯模糊的时间影响最大的是以下两个因素:(1)模糊半径;(2)像素点数量(图片大小)
高斯模糊的公式以及理解
高斯模糊之所以叫高斯模糊,是因为它运用了高斯的正态分布的密度函数。
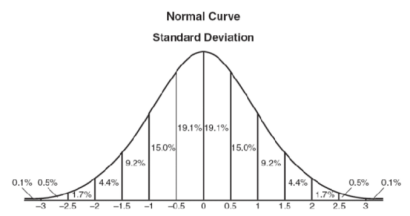
在图形上,正态分布是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。
如下图所示:
公式为:
其中,μ是x的均值,σ是x的标准差(评论提醒)。由于每次计算都以当前计算点为原点,所以μ等于0。于是公式进一步简化为:
计算平均值的时候,我们只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。
N维高斯函数的通项公式:
里面的参数中,r就是模糊半径,而在二维坐标系中,模糊半径就是x^2+y^2,σ 是正态分布的标准偏差,所以代入通项公式我们就可以得到二维的高斯函数公式。
将N=2带入得到二维高斯函数的方程:
二维高斯函数公式生成的曲面的高线是从中心开始以正态分布辐向的同心圆.不为零的像素组成的矩阵(卷积)在原来的图像矩阵像素作做变换,每个像素的值都是相邻一圈的像素值的加权平均数.
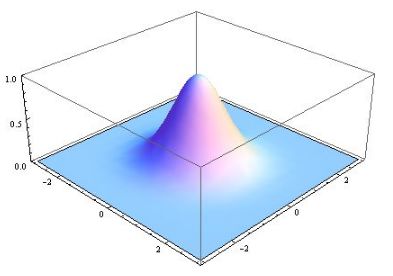
图形表示如下图所示:
本质上,图像的模糊就是将(灰度)图像I和一个高斯核进行卷积操作:
其中“*”表示卷积操作;
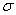
高斯模糊通常是其他图像处理操作的一部分,比如图像插值操作、兴趣点计算以及很多其他应用。
SciPy有用来做滤波操作的scipy.ndimage.filters模块。该模块使用快速一维分离的方式来计算卷积。
对于灰度图像,我们进行高斯模糊时采用如下代码:
from PIL import Image
import numpy as np
from scipy.ndimage import filters
from matplotlib import pyplot as plt
im = np.array(Image.open(u'test.jpg').convert('L'))
im2 = filters.gaussian_filter(im, 3)
im3 = filters.gaussian_filter(im, 5)
plt.subplot(1, 3, 1)
plt.axis('off')
plt.imshow(im, cmap='gray')
plt.title('original')
plt.subplot(1, 3, 2)
plt.axis('off')
plt.imshow(im2, cmap='gray')
plt.title('gaussian(kernel 3)')
plt.subplot(1, 3, 3)
plt.axis('off')
plt.imshow(im3, cmap='gray')
plt.title('gaussian(kernel 5)')
plt.show()
输出结果为:
对于彩色图像,我们进行高斯模糊时采用如下代码:
from PIL import Image
import numpy as np
from scipy.ndimage import filters
from matplotlib import pyplot as plt
im = np.array(Image.open(u'test.jpg'))
im2 = np.zeros(im.shape)
im3 = np.zeros(im.shape)
for i in range(3):
im2[:, :, i] = filters.gaussian_filter(im[:, :, i], 3)
im3[:, :, i] = filters.gaussian_filter(im[:, :, i], 5)
im2 = np.uint8(im2) # color
im3 = np.uint8(im3)
fig = plt.figure(figsize=(15, 15))
plt.subplot(1, 3, 1)
plt.axis('off')
plt.imshow(im)
plt.title('original')
plt.subplot(1, 3, 2)
plt.axis('off')
plt.imshow(im2)
plt.title('gaussian(kernel 3)')
plt.subplot(1, 3, 3)
plt.axis('off')
plt.imshow(im3)
plt.title('gaussian(kernel 5)')
plt.show()
输出结果为:

上面gaussian_filters()函数的最后一个参数表示标准差。
图中显示了随着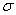
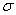
上面的脚本中,并不总是需要将图像转换成uint8格式,这里只是将像素值用八位来表示。
关于该模块更多的内容以及不同的参数选择,请查看http://docs.scipy.org/doc/scipy/reference/ndimage.html上SciPy文档中的scipy.ndimage部分。
参考文献:
python计算机视觉编程:http://yongyuan.name/pcvwithpython/
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域26个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请扫一扫如下二维码关注我们的公众号,获取人工智能的专业知识!
请加专知小助手微信(Rancho_Fang),加入专知主题人工智能群交流!加入专知主题群(请备注主题类型:AI、NLP、CV、 KG等)交流~
点击“阅读原文”,使用专知