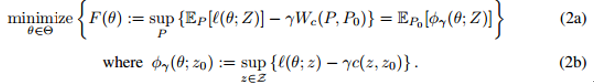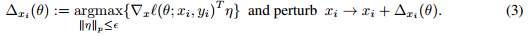【ICLR2018 最高分论文】利用分布鲁棒优化方法应对对抗样本干扰
点击上方“专知”关注获取专业AI知识!
【导读】近日,深度学习顶会ICLR2018评审结果出炉,得分最高的论文是 《Certifiable Distributional Robustness with Principled Adversarial Training》,得到的是9,9,9的高分,三个评审人都给出了非常肯定的评价,这篇论文主要是针对在有对抗样本时,神经网络会非常脆弱,训练集中有个别的对抗样本常常就会导致训练的模型完全失效的问题,如何利用神经网络学到鲁棒的数据分布是一个非常重要的研究方向,论文提出一种称作分布鲁棒优化的方法来确保模型在有对抗样本干扰情况下仍然有很好的表现。以下是相关论文介绍。
当前,我们在利用神经网络来学习数据的分布。 对于回归/分类问题, 我们学习已知数据关于类别信息的分布, 对于GAN等, 我们直接学习数据的分布。
然而,在有对抗样本的时,神经网络非常脆弱,训练集中有个别的对抗样本常常就会导致训练的模型完全失效。因此, 利用神经网络学到的鲁棒的数据分布是非常重要的 。
对于分布,考虑对真实数据分布单位Wasserstein球内(关于Wasserstain散度, 参见Wiki)扰动的拉格朗日惩罚,文章提出了一种考虑最坏的训练数据扰动情况下模型参数的更新规则, 称作分布鲁棒优化。
在这样的模型求解机制下, 我们可以确保模型在有对抗样本干扰情况下仍然有很好的表现。传统的SMT方法可以得到类似的稳定的分布, 但是由于计算成本太高无法在实践中应用。本文提出的训练机制在损失函数光滑时,相比于通常基于经验损失的目标函数, 几乎不会增加计算和统计的代价。
论文:Certifiable Distributional Robustness with Principled Adversarial Training
▌摘要
由于神经网络容易受到对抗样本的干扰,因此研究人员提出了许多启发式的攻击和防御机制。我们采用分布鲁棒优化的观点,保证对抗输入干扰下网络的性能。通过考虑拉格朗日惩罚公式在Wasserstein ball的源数据分布上的干扰,我们提供了一个训练过程,增强了训练数据在最坏情况干扰下的模型参数更新。对于光滑损失,我们的方法在保证中等程度的鲁棒性的同时,具有很小的计算或统计成本。此外,我们的统计保证我们的整体损失具有鲁棒性。我们达到或超越了监督和强化学习任务中的启发式方法。
▌详细内容
神考虑经典的监督分类问题,我们最小化参数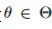
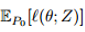
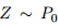
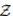
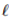
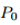
然而,最近的研究表明,神经网络很容易受到对抗例子的影响;似乎无法察觉的对数据的干扰会导致模型的错误,例如,输出错误的分类。随后,很多研究人员提出了对抗攻击和防御机制。虽然这些工作为对抗训练提供了初步的基础,但是对于提出的白盒攻击是否能够找到最有敌意的干扰以及这样的防御能否成功阻止的一类攻击没有保证。另一方面,使用SMT解决方案对深层网络进行验证,在鲁棒性方面提供了正式的保证,但总的来说是困难的(NP-hard);这种方法即使在小型网络上也需要高昂的计算费用。
我们从分布鲁棒性优化的角度出发,提供了一个对抗训练过程,其计算和统计性能得到了保证。我们假设数据生成的分布Z〜P0的一个分布类别为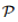
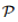
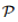
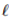
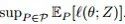
我们简要概述一下我们的方法。令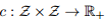
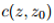
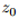

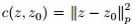
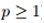
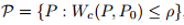
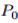
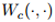
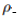
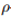
我们已经用较鲁棒的代替损失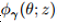
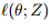
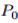
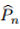
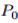
惩罚问题(2)的关键特征是,对于平滑损失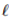
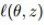
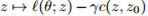
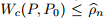
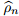
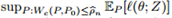
鲁棒的优化和对抗训练
标准的鲁棒性优化方法是最小化损失函数
的值,其中
是一些不可靠的集合。不幸的是,这种方法有局限性,除了特殊的结构损失,如线性和简单的凸函数的组成函数。然而,这种鲁棒的方法成为最近对抗训练的基础,对抗训练在一个随机的过程中,会考虑到噪声数据优化过程。有一种这样的探索研究,利用局部线性损失函数(提出
,称为“快速梯度符号法”(Goodfellowet al. 2015))
一种形式的对抗训练只简单训练受干扰的损失(Goodfellow et al., 2015; Kurakin et al., 2016),这种方法有很多其他的变体(Papernot et al., 2016b; Tramer ` et al., 2017; Carlini & Wagner,2017; Madry et al., 2017). Madry et al. (2017),这些方法试图优化目标函数
,它是惩罚问题(2)的有约束版本。这种鲁棒的想法通常是难以处理的:u中内部最小上界通常是非凹的,所以目前还不清楚这些技术是否适合模型拟合,并且这些技术可能不能发现最坏的情况。事实上,当深度网络使用ReLU激活时,难以找到最坏的干扰情况,这表明快速迭代的启发是很难的(见引理2和附录B)。平滑度可以在指数线性单位的标准深层结构中获得(ELU),允许我们用低的计算成本来发现拉格朗日最坏的干扰。
分布式鲁棒性最优化。
为了对当前的工作进行定位,我们回顾了一些关于鲁棒性研究的工作。鲁棒目标(1)中
的选择既影响我们想要考虑的不确定性集合的丰富性,又影响最终优化问题的易处理性。先前的分布式鲁棒性方法已经考虑了对
进行有限维参数化,例如,对时间,支持,或方向偏差的约束集,以及诸如f-散度的概率测量的非参数距离,和Wasserstein距离。与对固定分布
提供有效支持的f-散度相比,
周围的Wasserstein ball包含不同支持的分布Q,并且允许(在某种意义上)对不可见的数据的鲁棒性。
许多学者研究了不确定集合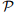
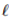
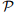
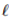
▌详细实验分析
实验图
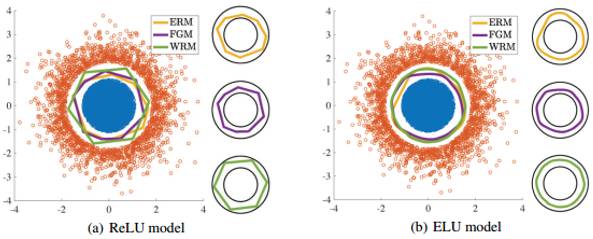
图1:在合成数据中的实验结果。训练数据用蓝色和橘红色展示。ERM、FGM和WRM的分类边界分别用黄色、紫色和绿色表示。这些边界显示的是训练数据与真正的类边界的分离。
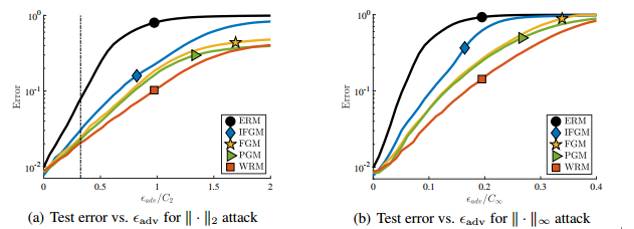
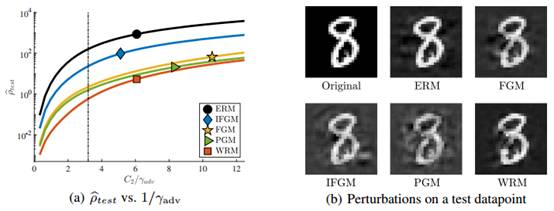
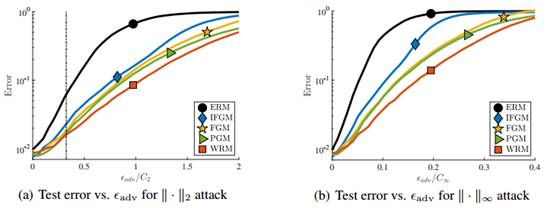
图2:MNIST数据集上PGM攻击。(a)和(b)展示测试分类的错误率,PGM攻击的对抗干扰水平
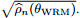
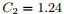
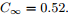
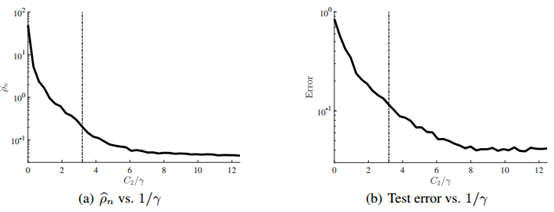
图3:损失表现的稳定性。在(a)中我们展示了给定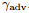
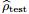
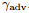
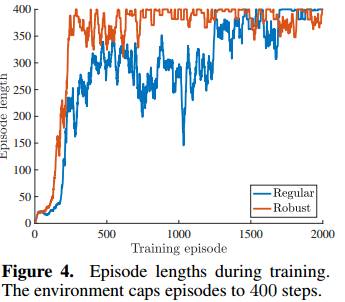
图4:训练期的Episode长度。环境上限为400步。
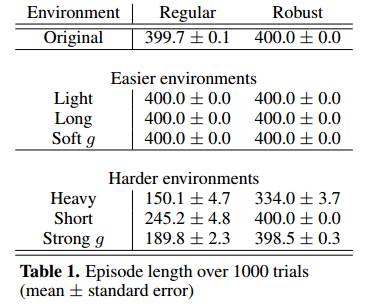
表1:超过1000次试验的Episode长度(平均值±标准误差)
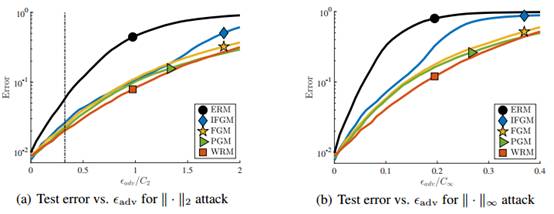
图5:在MNIST数据集上进行快速梯度攻击(Fast-gradient attacks)的结果。(a)和(b)展示测试分类的错误率,FGM攻击的对抗干扰水平
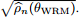
图6:在MNIST数据集上进行反复快速梯度攻击(Iterated Fast-gradient attacks)的结果。(a)和(b)展示测试分类的错误率,IFGM攻击的对抗干扰水平
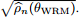
图7:可视化输入的稳定性。我们举例说明了使模型对数据点进行错误分类所需的最小WRM干扰(最大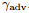
图8:(a)稳定性;(b)固定对手的测试错误(test error for a fixed adversary.)。我们用不同的γ训练WRM模型,并用一个固定的WRM对手干扰它们(竖线表示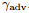
▌结论
形式(5)的显式分布式鲁棒性除了可以用在有限类的情况下,在其他情况下是难以处理的。我们提供了一种有效的保证分布鲁棒性的方法,它对于对抗数据干扰具有简单形式描述。只使用损失函数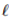
▌评论意见
1. 9分,在这篇非常好的论文中,我们的目标是利用鲁棒学习:不仅要将分布P_0进行风险最小化,而且还要对抗学习P_0周围的最坏情况分布的干扰。由于最小-最大问题一般是困难的,所以在这里实际研究的是这类问题的松弛(非严格的):有可能给出该问题的非凸对偶表述。如果对偶参数足够大,那么由于初始损失是平滑的,函数就变成了凸函数。接下来可证明的边界,针对分布ball范围内鲁棒学习和随机优化任务。实验表明,这样做的表现符合预期,并对于为什么会出现这种情况给出了一个很好的解释:分离线被从样本中“推开”,并且边缘似乎随着这个过程而增加。
2. 9分,本文将最近文献中的研究思想应用于鲁棒优化中,特别是使用Wasserstein度量的分布鲁棒优化,并且表明在鲁棒性要求不太高的平滑损失函数的框架下,所得到的优化问题与原来相比具有相同的难度水平(不考虑对抗攻击)。我认为这个想法是直观和合理的,结果是很不错的。虽然只有在强度较弱的情况下才有效,但在实践中,这相对于存在大偏差/敌手,似乎是更常见的情况。由于对抗训练是深度学习的重要课题,我觉得这项工作可能会导致为对抗训练提供有前途和原则的方法。
3. 9分,本文提出了一个有原则的方法来诱导训练神经网络的分布鲁棒性,目的是减轻对抗性样例的影响。这个想法是:训练这个模型使之不仅在未知的总体分布方面表现良好,而且在总体分布周围某些最坏情况分布表现良好。具体而言,作者采用Wasserstein距离来定义歧义集(ambiguity sets)。这使得他们可以使用分布的鲁棒优化文献中的强对偶结果,并将经验极小-极大问题表示为具有不同成本的正则化ERM。本文的理论得到了实验结果的支持。总的来说,这是一篇写得很好的论文,它创造性地结合了许多有趣的想法来解决一个重要的问题。
参考文献:
https://openreview.net/pdf?id=Hk6kPgZA-
https://openreview.net/forum?id=Hk6kPgZA-
请关注专知公众号(扫一扫最下面专知二维码,或者点击上方蓝色专知)
后台回复“CDR” 就可以获取本论文pdf下载~
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域25个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请扫一扫如下二维码关注我们的公众号,获取人工智能的专业知识!
请下方扫一扫专知小助手微信(Rancho_Fang),加入专知主题群(请备注主题类型:AI、NLP、CV、 KG等)交流~
点击“阅读原文”,使用专知!