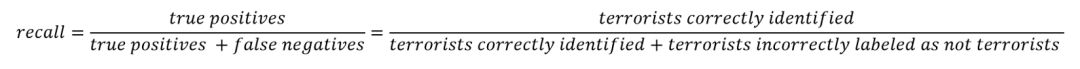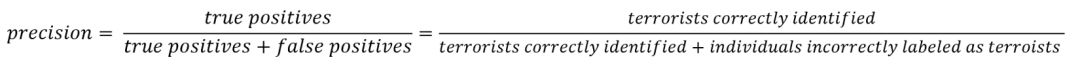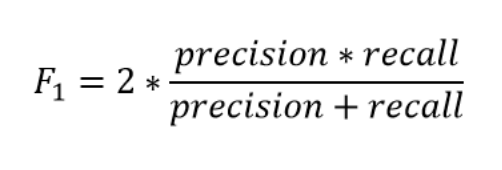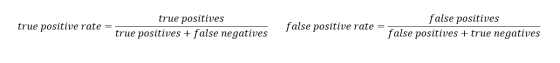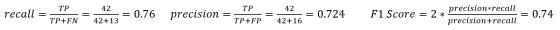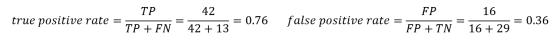【干货】不止准确率：为分类任务选择正确的机器学习度量指标（附代码实现）- 专知

【干货】不止准确率：为分类任务选择正确的机器学习度量指标（附代码实现）

【导读】本文是数据科学研究者William Koehrsen撰写的技术博文，介绍了在分类模型中需要用到的度量标准。我们知道，准确率是我们在分类任务中最常用到的度量指标，但是单纯的准确率并不能说明模型的整体性能。本文就举例介绍了分类任务中的其他度量标准，首先介绍一些相关概念：精确度、召回率、F1分数、TRP和FPR等。另外包括两种可视化方法：混淆矩阵和ROC曲线。相信通过本文，你能真正理解分类任务中的几种度量指标，并且能知道你获得一个均衡的分类模型。

Beyond Accuracy: Precision and Recall

为分类任务选择正确的度量标准

如果某个声称自己创造了一个模型, 能够以99％以上的准确率识别出要登机的人是不是恐怖分子, 你相信么? 其实确实有这样的模型：我们可以把每个从美国机场飞来的人都分为非恐怖分子(正常人)。由于每年美国航班的平均乘客数量为8亿人次(https://www.rita.dot.gov/bts/press_releases/bts018_16)，而从2000年至2017年登上美国航班的恐怖分子(被确认的)仅有19人(https://en.wikipedia.org/wiki/List_of_aircraft_hijackings#2000s)，该模型的准确率（accuracy）达到99.9999999％！这个模型的性能非常强悍，但是不用怀疑, 美国国土安全部肯定不会打电话来购买这个模型。虽然这个解决方案具有几乎完美的准确性. 但是仅仅用准确率（accuracy）这一个指标来评估模型是不够的！

识别恐怖分子的任务是一个典型的不平衡分类问题：我们需要确定两个类别: 恐怖分子以及正常人- 其中一个类别含有绝大多数样本。另一个不平衡的分类问题是检测人群发病率极低的疾病. 在这两种情况下，正例:健康人和非恐怖分子远远超过了负例: 发病和恐怖分子。这些问题在数据科学中比比皆是，显然准确率不是评估这些问题的好指标。

根据直觉, 我们知道把所有识别恐怖分子任务的样本都分成负例(正常人)，并没有什么意义，反而我们应该在识别正例上下功夫。直觉告诉我们, 我们应该最大化是召回率(Recall)，换句话说, 这是模型在数据集中查找所有有关这类样本的能力。召回率的确切定义是: 被正确识别成正例的数量除以被正确识别成正例的数量加上被错误识别成负例的数量。真阳性(True positives)是被模型预测为正的正样本，假阴性(False negatives)是被模型预测为负的正样本。在恐怖主义案例中，真阳性是被正确认定的恐怖分子，而假阴性将是模型预测不是恐怖分子，其实实际是恐怖分子的样本，模型预测错了。召回率可以被认为是模型能够找到数据集中所有感兴趣样本的能力。

注意到这个等式：如果我们把所有的样本都标记为恐怖分子，那么我们的召回率就会达到1.0！我们有一个完美的分类器吗？不完全是。与数据科学中的大多数概念一样，我们选择最大化这两类指标进行权衡。在这一情况下，当我们增加召回率时，我们会降低精度。再次，我们直觉地认为，将100％的乘客标记为恐怖分子的模型可能没有用处，因为我们将不得不禁止每个人飞行。我们直观地可以看到：这个新模型会有很低的精确度（precision）。

精确度（precision）定义是：真阳性数除以真阳性数加假阳性数。假阳性是指模型错误地将预测样本标记为正确的，而实际上它是错误的。虽然召回率表示能够在数据集中查找所有相关实例，但精确度表达我们模型预测正确的样本数目中真正正确的比例。

现在，我们可以看到，我们将所有个人都归类为非恐怖分子的第一种模式并不是很有用。虽然它具有接近完美的准确性，但它具有0精度和0召回，因为没有true positives！假设我们稍微修改模型，并将一个人正确识别为恐怖分子。现在，我们的精确度将为1.0（没有误报false positives），但我们的召回率会很低，因为我们仍然会有很多漏报（False Negative）。如果我们走到另一个极端，将所有乘客归类为恐怖分子，我们将召回1.0。我们会抓住每一个恐怖分子 - 但我们的精确度会很低，我们会扣留许多无辜的人。换句话说，随着我们提高精度，我们降低了召回，反之亦然。

▌结合精确度和召回率

在某些情况下，我们可能知道我们想要以牺牲另一个度量为代价来最大化召回或精度。例如，在对患者进行初步疾病筛查以进行随访检查时，我们可能会希望患者的召回接近1.0 - 我们希望找到所有真正患有该疾病的患者 - 并且如果后续检查的成本低，我们可以接受较低的精确度，因为后续检查并不重要。但是，如果我们想要找到精度和召回的最佳组合，我们可以使用所谓的F1 score来组合这两个度量。

F1 score是精确度和召回率的调和平均值（harmonic mean），其考虑了以下等式中的两个度量：

我们使用调和平均值而不是简单平均值，因为它会惩罚极端值。精度为1.0且召回率为0.0的分类器的简单平均值为0.5，但F1分数为0。F1分数给出了两种测量值的相同权重，并且是一般Fβ度量的具体示例，其中β可以调整为给予召回或精确度更多的权重。（还有其他一些结合精度和召回率的指标，如精度和召回率的几何平均值，但F1 score是最常用的。）如果我们想创建一个平衡的分类模型，并具有召回和精确度的最佳平衡，那么我们尝试最大化F1 score。

▌可视化精度和召回率

我已经抛出了一些新的术语，我们将通过一个示例来演示如何在实践中使用它们。在我们到达那里之前，我们需要简要地谈谈用于显示精确度和召回率的两个概念。

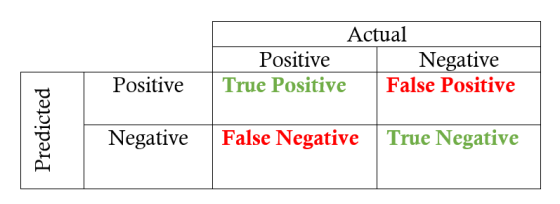
首先是混淆矩阵（confusion matrix），它有助于快速计算模型中预测标签的精度和查全率。二元分类的混淆矩阵显示了四种不同的结果：true positive（真阳性）, false positive（假阳性，可以称作误报率）, true negative（真阴性）, and false negative（假阴性，可以称作漏报率）。Actual实际值形成列，predicted预测值（标签）形成行。行和列的交集显示四个结果中的一个。例如，如果我们一个样本被预测为正样本，但实际上是负样本，那么这是一个false positive（假阳性，即误报）。

从混淆矩阵到召回率和精确度需要找到矩阵中的各个值并应用等式：

显示分类模型性能的另一个主要Receiver Operating Characteristic（ROC）曲线。这个想法相对简单：ROC曲线显示了在我们的模型在判别正样本时改变其阈值，召回率与精度的关系如何变化。阈值表示在正类中数据点被预测的值。如果我们有一个识别疾病的模型，我们的模型可能会为0到1之间的每个患者输出一个分数，我们可以在此范围内设置一个阈值来标记患者患有该疾病（正负标签）。通过改变阈值，我们可以尝试达到正确的精度与召回平衡。

其一是真正类率(true positive rate ,TPR), 计算公式为TPR=TP/ (TP+ FN)，刻画的是分类器所识别出的正实例占所有正实例的比例。另外一个是负正类率(false positive rate, FPR),计算公式为FPR= FP / (FP + TN)，计算的是分类器错认为正类的负实例占所有负实例的比例。还有一个真负类率（True Negative Rate，TNR），也称为specificity,计算公式为TNR=TN/ (FP+ TN) = 1-FPR。这两个都可以从混淆矩阵中计算出来：

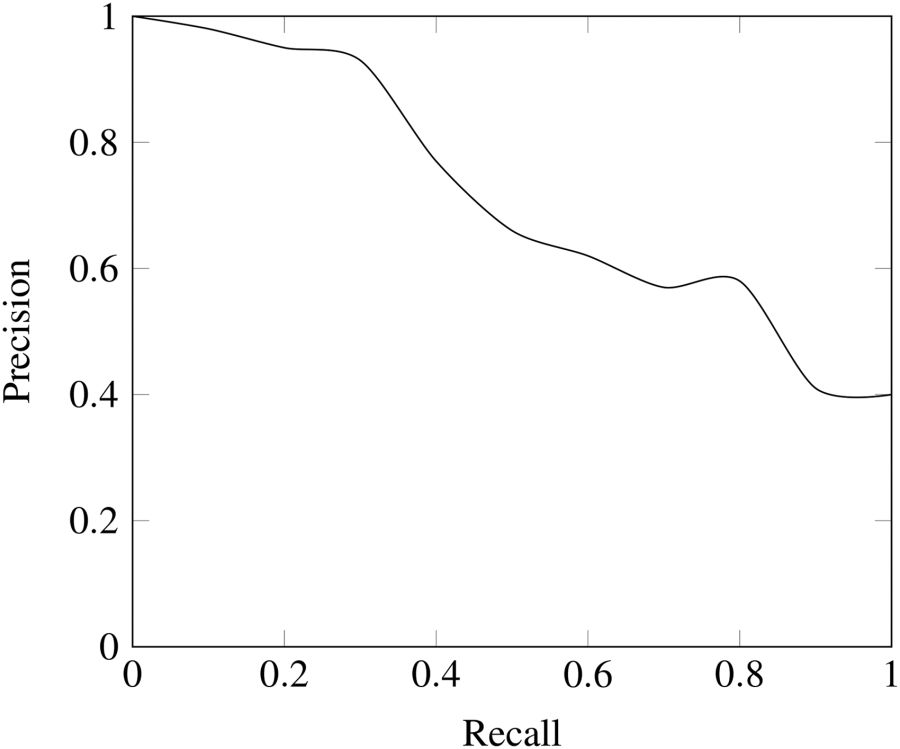
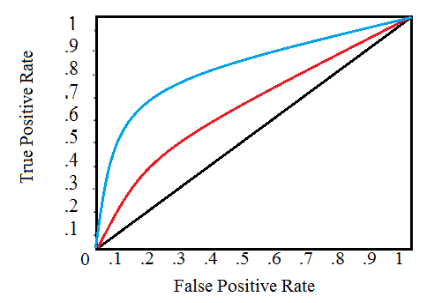
典型的ROC曲线如下所示：

黑色对角线表示随机分类器，红色和蓝色曲线表示两种不同的分类模型。对于一个给定的模型，我们只能保持在一条曲线上，但我们可以通过调整对正例分类的阈值来沿曲线移动。通常，当我们降低阈值时，我们沿着曲线向右和向上移动。阈值为1.0时，我们将位于图的左下角，因为我们没有将数据点预测为阳性，导致没有true positives，也没有false positives（TPR = FPR = 0）。当我们降低阈值时，我们将更多的数据点标识为正数，得到更多true positives，但也更多的false positives（TPR和FPR增加）。最终，在0.0的阈值处，我们将所有数据点标识为正，并且发现自己处于ROC曲线的右上角（TPR = FPR = 1.0）。

最后，我们可以通过计算曲线下的总面积（AUC）来量化模型的ROC曲线，该曲线下降的范围在0到1之间，度量值越高表明分类性能越好。在上图中，蓝色曲线的AUC将大于红色曲线的AUC，这意味着蓝色模型更好地实现了精确度和召回率的混合。随机分类器（黑线）AUC达到0.5。

▌总结

本文涵盖了一些术语，其中每一个都不难理解，但是组合起来就有点复杂。回顾一下，然后通过一个例子来加深了解我们学到的新想法。

二元分类的四个结果

• True positives真阳性：样本点标记为正，实际上是正

• False positives假阳性：样本点标记为正，实际上是负，可以称作误报率

• True negatives真阴性：标记为负数的样本点实际上是负数

• False negatives假阴性：标记为负数的样本点实际上是正数，可以称作漏报率

召回率和精确率

• Recall召回率：分类模型识别所有相关实例的能力，又称“查全率”；

• Precision精确度：分类模型仅返回相关实例的能力，也称准确率

• F1 score：使用调和平均值结合召回率和精确度的单一度量

可视化召回和精确度

• Confusion matrix混淆矩阵：显示来自分类问题的实际标签和预测标签

• Receiver operating characteristic（ROC）曲线：将真正类率（TPR）与负正类率（FPR）作为模型阈值的函数进行绘制。

• 曲线下面积（AUC）：根据ROC曲线下面积计算分类模型总体性能的度量

▌应用示例

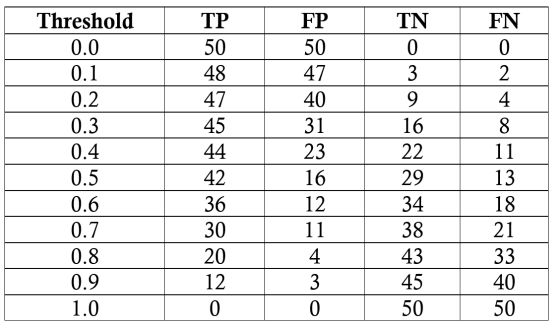
我们的任务是诊断100名患者，其中50%的人是普通人群。我们将假设一个黑匣子模型，在这里我们输入关于患者的信息并得到介于0和1之间的分数。我们可以改变病人的标记为阳性（有疾病）的阈值，以最大限度地提高分类器的性能。我们将以0.1为增量评估阈值从0.0到1.0模型的性能，每一步计算ROC曲线上的精度，召回率，F1和在ROC曲线的位置。以下是每个阈值的分类结果：

我们将在0.5的阈值处对召回率，精确度，真正类率（TPR）与负正类率（FPR）进行一次样本计算。首先我们得到混淆矩阵：

我们可以使用矩阵中的数字来计算召回率，精度和F1分数：

然后我们计算真正类率（TPR）与负正类率（FPR），找出ROC曲线的y和x坐标。

为了制作整个ROC曲线，我们在每个阈值处执行此过程。这非常乏味，所以我们不用手工完成，而是使用像Python这样的语言来为我们做到这一点！。我们在Github开源了实现这个的代码。

链接：

https://github.com/WillKoehrsen/Data-Analysis/blob/master/recall_precision/recall_precision_example.ipynb

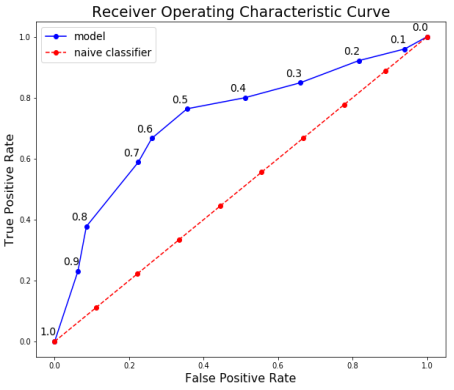
最终的ROC曲线如下所示，并在点上方设置阈值。

在这里我们可以看到将所有结果聚集在一起的曲线！在1.0的阈值，我们没有将患者分类为患有该疾病，因此召回率和精确度是0.0。随着阈值的降低，召回率会增加，因为我们发现更多患有该疾病的患者。然而，随着我们的召回率增加，我们的精确度下降，因为除了增加真阳性外，我们还增加了假阳性。在0.0的阈值，我们的召回率是完美的 - 我们能发现所有患有该疾病的患者 - 但我们的精确度很低，因为有很多误报。通过改变阈值并选择最大化F1分数的阈值，我们可以沿着给定模型的曲线移动。为了改变整个曲线，我们需要建立一个不同的模型。

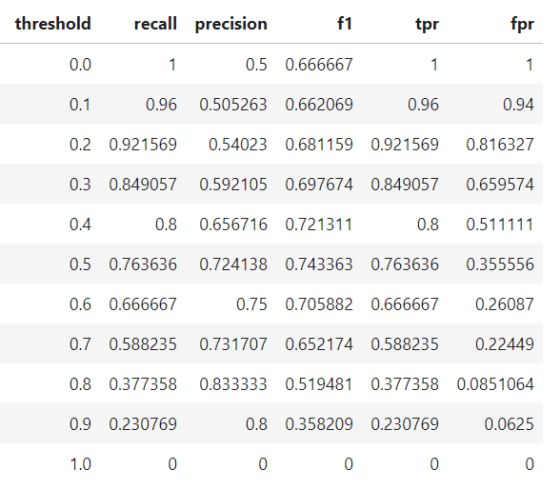
每个阈值的最终模型统计如下：

▌详细代码：

第一步：Recall and Precision Diagnostic Example

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
% matplotlib
inline

import seaborn as sns

from IPython.core.pylabtools import figsize

figsize(10, 8)

第二步：Confusion Matrix Numbers

results = pd.DataFrame({'threshold': [0.0, 0.1, 0.2, 0.3, 0.4,0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
                        'tp': [50, 48, 47, 45, 44, 42, 36,  30,  20, 12, 0],
                        'fp': [50, 47, 40, 31, 23, 16, 12,  11,   4,  3, 0],
                        'tn': [0,   3,  9, 16, 22, 29, 34,  38,  43, 45,50],
                        'fn': [0,   2,  4,  8, 11, 13, 18,  21, 33, 40, 50]
                       })

第三步：Calculate Precision, Recall, F1, TPR, FPR

def calculate_metrics(results):
    roc = pd.DataFrame(index=results['threshold'], columns=['recall', 'precision', 'f1',
 'tpr', 'fpr'])

    for i in results.iterrows():
        fn, fp, t, tn, tp = i[1]
        assert tp + fp + tn + fn == 100, 'Patients must add up to 100'

        recall = tp / (tp + fn)

        if tp == fp == 0:
            precision = 0
            true_positive_rate = 0

        else:
            precision = tp / (tp + fp)
            true_positive_rate = tp / (tp + fn)

        if precision == recall == 0:
            f1 = 0
        else:
            f1 = 2 * (precision * recall) / (precision + recall)

        false_positive_rate = fp / (fp + tn)

        roc.ix[t, 'recall'] = recall
        roc.ix[t, 'precision'] = precision
        roc.ix[t, 'f1'] = f1
        roc.ix[t, 'tpr'] = true_positive_rate
        roc.ix[t, 'fpr'] = false_positive_rate

    return roc


roc = calculate_metrics(results)
roc.reset_index()

第四步：Receiver Operating Characteristic Curve

figsize(10, 8)
plt.style.use('seaborn-dark-palette')
thresholds = [str(t) for t in results['threshold']]
plt.plot(roc['fpr'], roc['tpr'], 'bo-', label='model');
plt.plot(list(np.linspace(0, 1, num=10)), list(np.linspace(0, 1, num=10)), 'ro--', 
label='naive classifier');
for x, y, s in zip(roc['fpr'], roc['tpr'], thresholds):
    plt.text(x - 0.04, y + 0.02, s, fontdict={'size': 14});

plt.legend(prop={'size': 14})
plt.ylabel('True Positive Rate', size=16);
plt.xlabel('False Positive Rate', size=16);
plt.title('Receiver Operating Characteristic Curve', size=20);