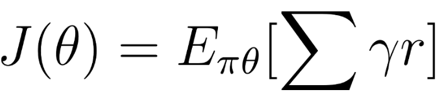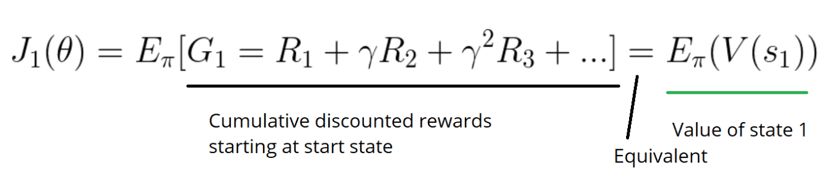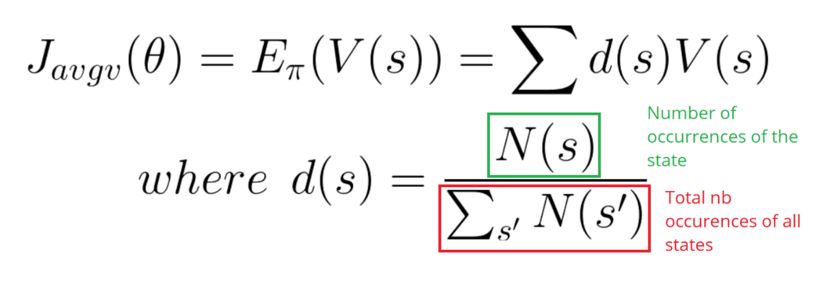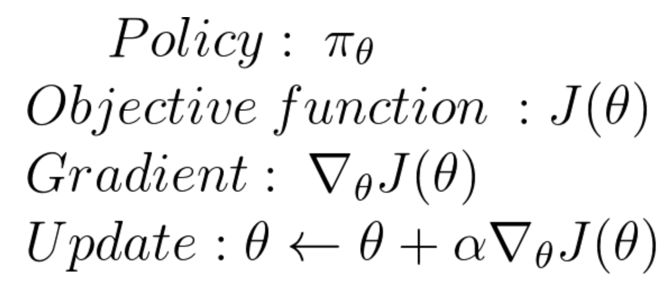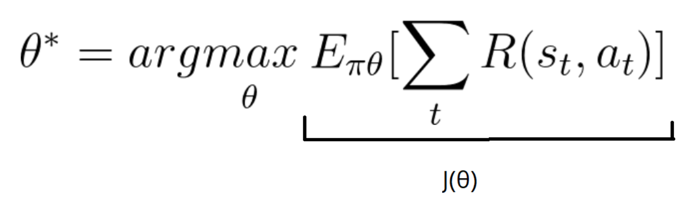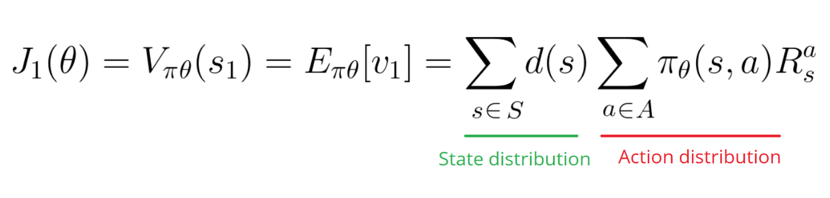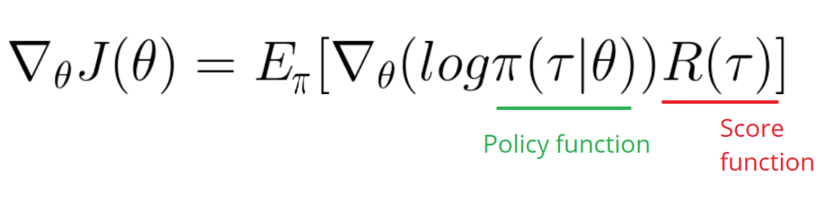强化学习:Policy-based方法Part2
【导读】在Part1部分,我们学习了什么是策略梯度,以及该算法的优势与劣势,在Part2部分,我们将学习到如何通过策略搜索实现策略函数的迭代优化。
作者|Thomas Simonini
编译|专知
整理|Yongxi
【攻克Dota2基础算法】深度Q学习介绍
强化学习:Policy-based方法 Part 1
目前,我们已经知道了基于策略的方法具有求解稳定、搜索效果好、以及始终保持一定的随机探索几率等优势。在本节,将首先从数学角度对相关理论知识给出解答,并给出基于TensorFlow的实现过程。
【策略搜索】
我们已经知道策略π是一个参数化函数,其结果是可以输出动作分布。
但如何评估策略是否是好的呢?策略可以被看作是一个优化问题,我们必须找到最佳的参数θ,来到达最大的分数函数,J(θ)。
这里有两个步骤:
通过策略评分函数J来测量策略的质量
使用策略梯度上升来找到最佳的策略参数,来增强我们的策略。
这个想法是,评分函数将告诉我们策略是否是好的。策略梯度上升将帮助我们找到最优的策略参数。
第一步:策略评分函数
我们使用目标函数的方法来评估策略函数的好坏。三种方法对策略优化来说都差不多,具体选择要取决于所处环境与目标。
首先,在一个回合环境中,我们可以使用起始值。计算第一次时间步的收获值(G1)。
如果我总是从状态S1开始,那么在整个过程中将能得到多少奖励呢?我们希望找出能最大化G1的策略,以帮助策略优化。
例如,在BreakOut中,当我重新开局时,这一回合总是从相同状态开始。
我们使用J1(θ)计算了分数,打掉20个砖块已经很不错了,但我仍希望能提升分数,为了完成一个目标,我需要提高行为奖励的概率分布。
在连续的环境中,我可以使用均值进行计算,以摆脱对某个特殊起始状态的依赖。每个状态价值通过概率被分别权重化(由于某些值比其他出现的更频繁)。
最后,我们可以使用没有时间步的平均奖励。这个想法主要是希望获得每个时间的最大奖励。
第二步:策略梯度上升
我们已经有了一个策略分数来告诉我们策略是不是足够好。接下来,希望找出参数θ,来最大化得分函数,这就意味着要找出最优化策略。
这一步可以通过在策略参数上执行梯度上升来完成。梯度上升是梯度下降的相反做法,只要记住梯度指向了函数的最陡峭改变的方向就可以很容易的理解。
在梯度下降过程中,我们找出函数的最陡峭的递减方向,而在梯度上升过程中,找出的是函数最陡峭的提高方向。
当需要最小化损失函数时,一般采用梯度下降;而在最大化目标函数时,一般采用梯度上升。
这一步的主要目的是找出梯度最快的提升路径,并沿着该路径进行迭代,优化策略函数。
接下来,将通过数学手段对其实现,这一部分有点难,但这是理解策略梯度上升算法的关键一步。
我们的目标是希望找出最好的θ*,进而最大化分数:
我们的得分函数可以被定义为如下公式:
这个公式意味着对所有策略期望奖励进行累加。
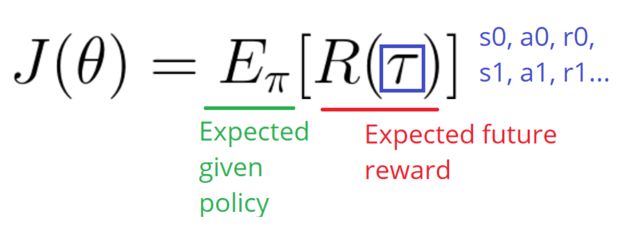
现在,由于我们希望完成梯度上升,所以需要对得分函数进行区分。得分函数定义为如下公式的形式:
我们知道,策略参数会对行为的选择方式、结果、汇报、状态、频率等产生影响。因此,以一种确定性的方式来保证策略的提升是非常有难度的。这是由于在那些选择的瞬间,性能很大程度上依赖了行为选择与状态分布。
这两个都会受到策略参数的影响。策略参数对行为的影响很容易找到,但如何找到其对状态分布的影响呢?
因此,我们面临一个问题,当梯度依赖于很多位置因素的情况下,该如何去估计各个策略的梯度呢?
解决方案是采用策略梯度定理。这为我们提供了一个不需要对状态分布微分的梯度表达方法。
需要注意的是,我们处在一种随机策略之下,这意味着策略输出的概率分布是π(τ;θ),进而通过考虑目前参数θ,来讲一系列的步骤进行输出。
但是对一个概率函数进行微分特别困难,除非可以把它变成对数形式,这回简化求导过程。
现在,将累加转换回期望:
如你所见,接下来,便只需要计算这个公式即可。现在,我们可以得出策略梯度的结论为:
这个策略梯度告诉我们,为了得到较高的评分,应该如何改变策略分布的参数。
R(tau)类似于标量分数:
如果R(tau)很高,这就意味着行动会带来高回报,则需要提高该动作出现的概率。
另一方面,如果R(tau)很低,便需要降低该行为出现的概率。
策略梯度将逐步朝着最有利的方向移动,以得到最高的汇报。
蒙特卡洛策略梯度:
在notebook中,我们将使用这个方法去设计策略梯度算法。由于我们的任务可以被拆分为一个个的回合,所以可以使用蒙特卡洛方法:
但是我们将面对该算法那的一个问题,由于我们仅仅在回合结束时才计算了R,并对所有的行为取平均。即使某些行为的结果非常差,如果平均分很高的话,可能也会认为这些行为都是很好的。
所以为了得到正确的策略,需要进行很多次采样,这就导致了学习的过程很漫长。
具体代码可参见如下链接【1】【2】.
[1] https://gist.github.com/simoninithomas/7a3357966eaebd58dddb6166c9135930#file-cartpole-reinforce-monte-carlo-policy-gradients-ipynb
[2] https://gist.github.com/simoninithomas/be159fc279cb1e927eec50e85f7483a0#file-doom-reinforce-monte-carlo-policy-gradients-ipynb
原文链接:
https://medium.freecodecamp.org/an-introduction-to-policy-gradients-with-cartpole-and-doom-495b5ef2207f
-END-
专 · 知
人工智能领域26个主题知识资料全集获取与加入专知人工智能服务群: 欢迎微信扫一扫加入专知人工智能知识星球群,获取专业知识教程视频资料和与专家交流咨询!
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请加专知小助手微信(扫一扫如下二维码添加),加入专知主题群(请备注主题类型:AI、NLP、CV、 KG等)交流~
请关注专知公众号,获取人工智能的专业知识!
点击“阅读原文”,使用专知