【2019年末硬货】深度学习的最优化:理论和算法综述论文，60页pdf257篇文献- 专知

【2019年末硬货】深度学习的最优化:理论和算法综述论文，60页pdf257篇文献

【导读】深度学习理论是当下研究的热点之一。最近来自UIUC计算机助理教授Sun Ruoyu撰写一篇深度学习最优化理论和算法的综述论文，共60页257篇文献，概述了神经网络的优化算法和训练理论《Optimization for deep learning: theory and algorithms》，并得到众多大佬的推荐，比如模仿学习带头人加州理工Yisong Yue，欢迎大家阅览，需要一番数学理论功底，方能扛过。

Ruoyu Sun

UIUC助理教授，研究优化和机器学习(尤其是深度学习)。我是FAIR的客座科学家。研究深度学习中的最优化，例如神经网络，GANs和Adam。本文将介绍《深度学习的最优化:理论与算法》的综述报告。另一个我一直在研究的方向是优化算法的计算/迭代复杂度，尤其是ADMM和坐标下降。

.https://ruoyus.github.io/

论文地址：

https://www.zhuanzhi.ai/paper/2a5e7596942977067240c946ecd4bd47

摘要

什么时候以及为什么能够成功地训练神经网络?本文概述了神经网络的优化算法和训练理论。首先，我们讨论了梯度爆炸/消失问题和更一般的不期望谱问题，然后讨论了实际的解决方案，包括仔细的初始化和归一化方法。其次，我们回顾了用于训练神经网络的一般优化方法，如SGD、自适应梯度方法和分布式方法，以及这些算法的现有理论结果。第三，我们回顾了现有的关于神经网络训练的全局问题的研究，包括局部极值的结果、模式连接、彩票假设和无限宽度分析。

1. 概述

本文的一个主要主题是了解成功训练神经网络的实际组成部分，以及可能导致训练失败的因素。假设你在1980年试图用神经网络解决一个图像分类问题。如果你想从头开始训练一个神经网络，很可能你最初的几次尝试都没有得到合理的结果。什么本质的变化使算法能有效进行?在高层次上，你需要三样东西(除了强大的硬件): 合适的神经网络、合适的训练算法和合适的训练技巧。

合适的神经网络。这包括神经结构和激活功能。对于神经结构，您可能想要用一个至少有5层和足够神经元的卷积网络来替换一个完全连接的网络。为了获得更好的性能，您可能希望将深度增加到20甚至100，并添加跳跃skip连接。对于激活函数，一个好的起点是ReLU激活，但是使用tanh或swish激活也是合理的。

训练算法。一个大的选择是使用随机版本的梯度下降(SGD)并坚持它。良好调整的步长足够好，而动量和自适应步长可以提供额外的好处。

训练技巧。适当的初始化对于算法的训练是非常重要的。要训练一个超过10层的网络，通常需要两个额外的技巧:添加规范化层和添加跳过连接。

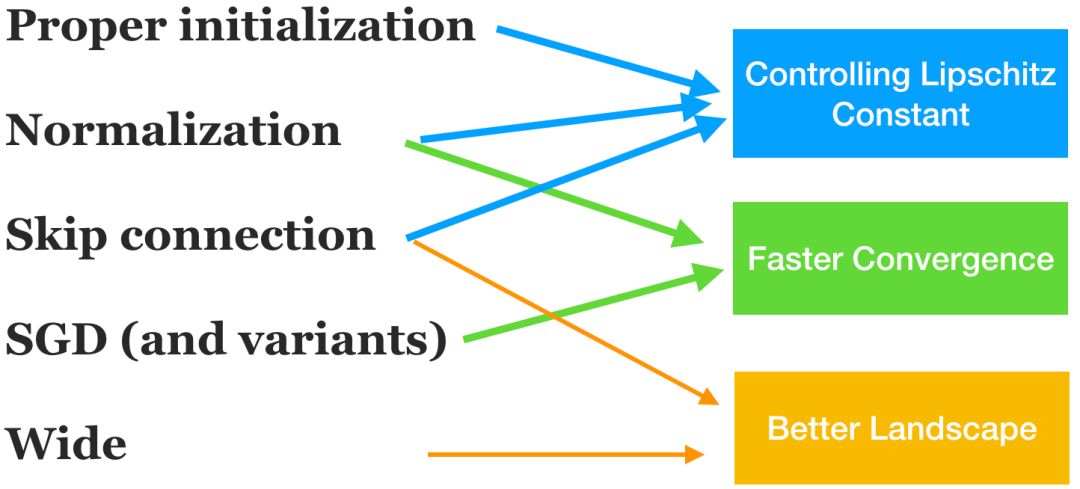
哪些设计选择是必要的?目前我们已经了解了一些设计选择，包括初始化策略、规范化方法、跳过连接、参数化(大宽度)和SGD，如图1所示。我们将优化优势大致分为三部分: 控制Lipschitz常数、更快的收敛速度和更好的landscape。还有许多其他的设计选择是很难理解的，尤其是神经架构。无论如何，似乎不可能理解这个复杂系统的每个部分，目前的理解已经可以提供一些有用的见解。

图1: 成功训练具有理论理解的神经网络的几个主要设计选择。它们对算法收敛的三个方面有影响:使收敛成为可能、更快的收敛和更好的全局解。这三个方面有一定的联系，只是一个粗略的分类。请注意，还有其他一些重要的设计选择，特别是神经体系结构，它们在理论上还没有被理解，因此在该图中被省略了。还有其他好处，比如泛化，也被忽略了。

为了使综述调查简单，我们将重点研究前馈神经网络的监督学习问题。我们将不讨论更复杂的公式，如GANs(生成对抗网络)和深度强化学习，也不讨论更复杂的体系结构，如RNN(递归神经网络)、attention和Capsule。在更广泛的背景下，监督学习理论至少包含表示、优化和泛化(参见1.1节)，我们不详细讨论表示和泛化。一个主要的目标是理解神经网络结构(由许多变量连接的参数化)如何影响优化算法的设计和分析，这可能会超越监督学习。

这篇文章是为那些对神经网络优化的理论理解感兴趣的研究人员写的。关于优化方法和基础理论的先验知识将非常有帮助(参见，[24,200,29]的准备)。现有的关于深度学习优化的调查主要针对一般的机器学习受众，如Goodfellow等[76]的第8章。这些综述通常不深入讨论优化的理论方面。相反，在这篇文章中，我们更多地强调理论结果，同时努力使它对非理论读者具有可访问性。如果可能的话，我们将提供一些简单的例子来说明这种直觉，我们将不解释定理的细节。

1.1 大景观：分解理论

分解是发展理论的一个有用且流行的元方法。首先简要回顾了优化在机器学习中的作用，然后讨论了如何分解深度学习的优化理论。

表示、优化和泛化。监督学习的目标是根据观察到的样本找到一个近似底层函数的函数。第一步是找到一个丰富的函数家族(如神经网络)，可以代表理想的函数。第二步是通过最小化某个损失函数来识别函数的参数。第三步是使用第二步中找到的函数对不可见的测试数据进行预测，产生的错误称为测试错误。测试误差可以分解为表示误差、优化误差和泛化误差，分别对应这三个步骤引起的误差。

在机器学习中，表示、优化和泛化这三个学科经常被分开研究。例如，在研究一类函数的表示能力时，我们往往不关心优化问题能否很好地解决。在研究泛化误差时，我们通常假设已经找到了全局最优值(概化调查见[95])。类似地，在研究优化属性时，我们通常不明确地考虑泛化误差(但有时我们假定表示误差为零)。

优化问题的分解。深度学习的优化问题比较复杂，需要进一步分解。优化的发展可以分为三个步骤。第一步是使算法开始运行，并收敛到一个合理的解，如一个固定点。第二步是使算法尽快收敛。第三步是确保算法收敛到一个低目标值的解(如全局极小值)。要获得良好的测试精度，还有一个额外的步骤，但是这超出了优化的范围。简而言之，我们将优化问题分为三个部分: 收敛性、收敛速度和全局质量。

大部分工作的回顾分为三个部分: 第四部分，第五部分和第六部分。大致说来，每个部分主要是由优化理论的三个部分之一。然而，这种划分并不精确，因为这三个部分之间的边界是模糊的。例如，第4节中讨论的一些技术也可以提高收敛速度，第6节中的一些结果解决了收敛问题和全局问题。划分的另一个原因是它们代表了神经网络优化的三个相当独立的子领域，并且在一定程度上是独立发展的。

1.2 文章结构

这篇文章的结构如下。在第二节中，我们提出了一个典型的监督学习神经网络优化问题。在第三节中，我们提出了反向传播(BP)，并分析了将经典收敛分析应用于神经网络梯度下降的困难。在第四节中，我们将讨论训练神经网络的神经网络特定技巧，以及一些基本理论。这些是神经网络相关的方法，打开了神经网络的黑盒子。特别地，我们讨论了一个主要的挑战，称为梯度爆炸/消失和一个更普遍的挑战，控制频谱，并回顾了主要的解决方案，如仔细的初始化和归一化方法。在第五节中，我们讨论了将神经网络视为一般非凸优化问题的泛型算法设计。特别地，我们回顾了SGD的各种学习速率调度、自适应梯度方法、大规模分布式训练、二阶方法以及现有的收敛和迭代复杂度结果。在第六节中，我们回顾了神经网络的全局优化研究，包括全局景观、模式连接、彩票假设和无限宽度分析(如神经正切核)。