专知-生成式对抗网络综述
一、 背景
1.1 深度学习、人工智能热潮
- 第一次浪潮:浅层学习
1980年代末期,用于人工神经网络的反向传播算法(也叫Back Propagation算法或者BP算法)的发明,给机器学习带来了希望,掀起了基于统计模型的机器学习热潮。这个热潮一直持续到今天。人们发现,利用BP算法可以让一个人工神经网络模型从大量训练样本中学习出统计规律,从而对未知事件做预测。这种基于统计的机器学习方法比起过去基于人工规则的系统,在很多方面显示出优越性。这个时候的人工神经网络,虽然也被称作多层感知机(Multi-layer Perceptron),但实际上是一种只含有一层隐层节点的浅层模型。
90年代,各种各样的浅层机器学习模型相继被提出,比如支撑向量机(SVM,SupportVector Machines)、Boosting、最大熵方法(例如LR, Logistic Regression)等。这些模型的结构基本上可以看成带有一层隐层节点(如SVM、Boosting),或没有隐层节点(如LR)。这些模型在无论是理论分析还是应用都获得了巨大的成功。相比较之下,由于理论分析的难度,加上训练方法需要很多经验和技巧,所以这个时期浅层人工神经网络反而相对较为沉寂。
2000年以来互联网的高速发展,对大数据的智能化分析和预测提出了巨大需求,浅层学习模型在互联网应用上获得了巨大成功。最成功的应用包括搜索广告系统(比如Google的AdWords、百度的凤巢系统)的广告点击率CTR预估、网页搜索排序(例如Yahoo!和微软的搜索引擎)、垃圾邮件过滤系统、基于内容的推荐系统等。
- 第二次浪潮:深度学习
2006年,加拿大多伦多大学教授、机器学习领域泰斗——Geoffrey Hinton和他的学生Ruslan Salakhutdinov在顶尖学术刊物《科学》上发表了一篇文章,开启了深度学习在学术界和工业界的浪潮。这篇文章有两个主要的信息:1. 很多隐层的人工神经网络具有优异的特征学习能力,学习得到的特征对数据有更本质的刻画,从而有利于可视化或分类;2. 深度神经网络在训练上的难度,可以通过“逐层初始化”(Layer-wise Pre-training)来有效克服,在这篇文章中,逐层初始化是通过无监督学习实现的。
自2006年以来,深度学习在学术界持续升温。斯坦福大学、纽约大学、加拿大蒙特利尔大学等成为研究深度学习的重镇。2010年,美国国防部DARPA计划首次资助深度学习项目,参与方有斯坦福大学、纽约大学和NEC美国研究院。支持深度学习的一个重要依据,就是脑神经系统的确具有丰富的层次结构。一个最著名的例子就是Hubel-Wiesel模型,由于揭示了视觉神经的机理而曾获得诺贝尔医学与生理学奖。除了仿生学的角度,目前深度学习的理论研究还基本处于起步阶段,但在应用领域已显现出巨大能量。2011年以来,微软研究院和Google的语音识别研究人员先后采用DNN技术降低语音识别错误率20%~30%,是语音识别领域十多年来最大的突破性进展。2012年,DNN技术在图像识别领域取得惊人的效果,在ImageNet评测上将错误率从26%降低到15%。在这一年,DNN还被应用于制药公司的DrugeActivity预测问题,并获得世界最好成绩,这一重要成果被《纽约时报》报道。 正如文章开头所描述的,今天Google、微软、百度等知名的拥有大数据的高科技公司争相投入资源,占领深度学习的技术制高点,正是因为它们都看到了在大数据时代,更加复杂且更加强大的深度模型能深刻揭示海量数据里所承载的复杂而丰富的信息,并对未来或未知事件做更精准的预测。
1.2 生成模型
1.2.3 马尔可夫链
1.3 生成模型评估方法
1.4 参考文献
- 深度学习-发展历程: [http://blog.sina.com.cn/s/blog_539819470102v5p0.html].
二、生成对抗网络基本模型
近年来,由于反向传播算法(Back Propagation)、DropOout算法、分段线性响应激活函数、批正则化(Batch Norma)等方法的提出,基于深度学习的判别式模型在广泛的应用中(比如图像分类、图像分割、目标跟踪等)均取得了极大地成功。传统的生成式模型大部分是基于最大化似然估计,然而概率密度的估计十分困难,这直接导致传统生成式模型难以计算和优化。
Goodfellow等人在2014年首次提出生成对抗网络框架,将博弈论中费零和博弈的思想与生成模型相结合,巧妙地避开的传统生成模型中概率密度估计困难等问题,使得生成模型达到了良好的效果。
下面我们将分别介绍对抗思想、生成模型,最后引出对抗生成网络,并给出一个简单的代码实现。
2.1 对抗思想
- 囚徒困境
1950年,由就职于兰德公司的梅里尔·弗勒德和梅尔文·德雷希尔拟定出相关困境的理论,后来由顾问艾伯特·塔克以囚徒方式阐述,并命名为“囚徒困境”。经典的囚徒困境如下:
警方逮捕甲、乙两名嫌疑犯,但没有足够证据指控二人有罪。于是警方分开囚禁嫌疑犯,分别和二人见面,并向双方提供以下相同的选择:
- 若一人认罪并作证检控对方(相关术语称“背叛”对方),而对方保持沉默,此人将即时获释,沉默者将判监10年。
- 若二人都保持沉默(相关术语称互相“合作”),则二人同样判监半年。
- 若二人都互相检举(互相“背叛”),则二人同样判监5年。
用表格描述如下: | | 甲沉默(合作) | 甲认罪(背叛) | ---|---|--- 乙沉默(合作) | row 1 col 2 | 甲即时获释;乙服刑10年 | 乙认罪(背叛) | row 2 col 2 | 二人同服刑5年 |
- 纳什均衡
如同博弈论的其他例证,囚徒困境假定每个参与者(即“囚徒”)都是利己的,即都寻求最大自身利益,而不关心另一参与者的利益。那么囚徒到底应该选择哪一项策略,才能将自己个人的刑期缩至最短?两名囚徒由于隔绝监禁,并不知道对方选择;而即使他们能交谈,还是未必能够尽信对方不会反口。就个人的理性选择而言,检举背叛对方所得刑期,总比沉默要来得低。试设想困境中两名理性囚徒会如何作出选择:
- 若对方沉默、我背叛会让我获释,所以会选择背叛。
- 若对方背叛指控我,我也要指控对方才能得到较低的刑期,所以也是会选择背叛。
二人面对的情况一样,所以二人的理性思考都会得出相同的结论——选择背叛。背叛是两种策略之中的支配性策略。因此,这场博弈中唯一可能达到的纳什均衡,就是双方参与者都背叛对方,结果二人同样服刑5年。 这场博弈的纳什均衡,显然不是顾及团体利益的帕累托最优解决方案。以全体利益而言,如果两个参与者都合作保持沉默,两人都只会被判刑半年,总体利益更高,结果也比两人背叛对方、判刑5年的情况较佳。但根据以上假设,二人均为理性的个人,且只追求自己个人利益。均衡状况会是两个囚徒都选择背叛,结果二人判监均比合作为高,总体利益较合作为低。这就是“困境”所在。例子有效地证明了:非零和博弈中,帕累托最优和纳什均衡是互相冲突的。
2.2 生成模型和判别模型
机器学习的任务就是学习一个模型,应用这个模型,对给定的输入预测相应的输出。这个模型的一般形式为决策函数 $Y=f(x)$,或者条件概率分布:$ Y = argmax_YP(Y|X) $。 机器学习方法又可以分为生成方法和判别方法,所学到的模型分别称为生成模型(Generative Model)和判别模型(Discriminative Model)。
判别方法由数据直接学习决策函数 $f(X)$,或者条件概率分布$P(Y|X)$作为预测模型,即判别模型。 生成方法由数据学习联合分布$ P(X, Y)$,然后求出条件概率分布 $P(Y|X)$做预测的模型,即为生成模型,具体公式如下:$ P(Y|X) = \frac{P(X, Y)}{P(X)}$
相比于判别方法,生成模型更关注数据之间的内在联系,需要学习联合分布;而判别模型更关注于给定输入 $X$,模型应该预测怎么样的输出 $Y$。由生成模型可以推导出判别模型,反之则不能。
2.3 生成对抗网络
什么是对抗生成网络?用Ian Goodfellow自己的话来说:
生成对抗网络是一种生成模型(Generative Model),其背后基本思想是从训练库里获取很多训练样本,从而学习这些训练案例生成的概率分布。而实现的方法,是让两个网络相互竞争,‘玩一个游戏’。其中一个叫做生成器网络( Generator Network),它不断捕捉训练库里真实图片的概率分布,将输入的随机噪声(Random Noise)转变成新的样本(也就是假数据)。另一个叫做判别器网络(Discriminator Network),它可以同时观察真实和假造的数据,判断这个数据到底是不是真的。”
2.3.1 基本原理
生成对抗网络是一个强大的基于博弈论的生成模型学习框架。该模型由GoodFellow在2014年首次提出,结合了生成模型和对抗学习思想。生成对抗网络的目的是训练一个生成模型 $G(z; thetaG)$,给定随机噪声向量 $noise$,生成符合真实数据分布 $ p_{data}(x)$的样本。 $G$训练新号来自于判别器 $ D(x)$。 $ D(x)$的学习目标目是准确区分输入样本的来源(真实数据或生成数据), 而生成器 $D$ 的学习目标是生成尽可能真实的数据,使得判别器 $G$ 认为生成数据是真实的。整个模型使用梯度下降法进行训练,生成器和判别器可以根据特定的任务选择具体的模型,包括但不限于全连接神经网络(FCN)、卷积神经网络(CNN)、回归神经网络(RNN)、长短期记忆模型(LSTM)等。
2.3.2 结构框架
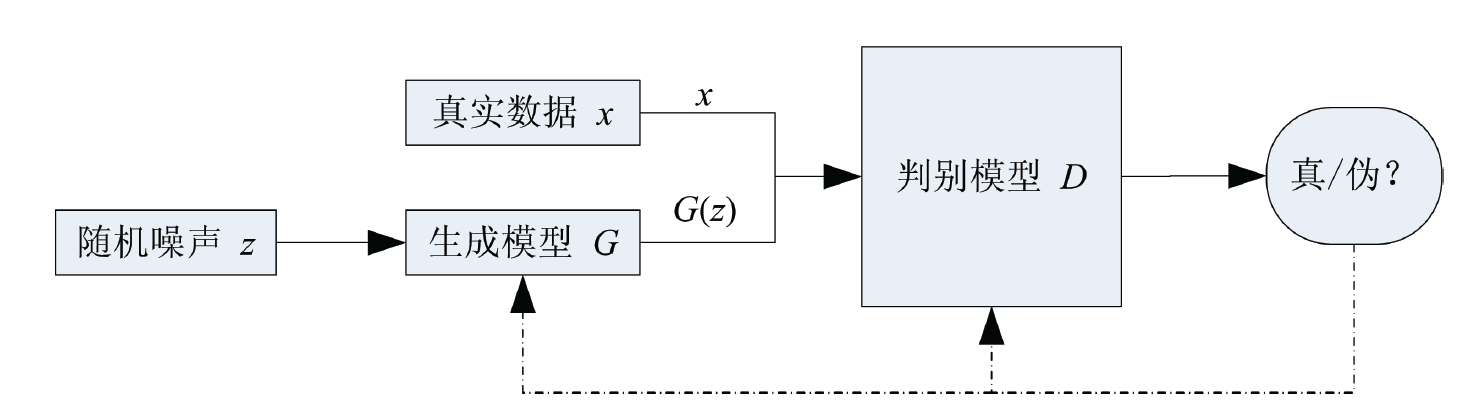
生成对抗网络的结构框架如下图所示。生成对抗网络主要有两部分构成,分别是生成器(Genernator Network)和判别器(Discriminator Network)。通过训练判别器$D$ 去最大化对真实样本(Real Samples)和生成样本(Fake Samples)判断的正确率,同时训练 生成器$G$ 去最小化判别器 $D$ 对生成样本判断的正确率,来优化生成器和判别器。也就是说,判别器$D$ 和生成器$G$ 进行零和博弈,优化目标的数学表达式如下: $$ min_G max_D V(D, G) = E_{x~p_{data}(x)}[logD(x)] + E_{noise~p_{noise}(noise)}[log(1-logD(noise))] $$
2.3.3 理论分析
待补充
2.4 代码实现
2.4.1 前言
- 环境配置
- Python 3.5
tensorflow 1.0+
完成代码
2.4.2 生成器(Gernreator)
def generator(noise, depth_list = [128, 784], is_training = True, is_reuse = False):
output = tf.convert_to_tensor(noise, tf.float32)
with tf.variable_scope('generator', reuse=is_reuse):
index = 1
counts_layer = len(depth_list)
for depth in depth_list:
in_dim = output.get_shape()[1].value
xavier_stddev = xavier_init(in_dim)
output = tf.layers.dense(output, depth, kernel_initializer=tf.random_normal_initializer(mean=0, stddev=xavier_stddev))
output = tf.layers.batch_normalization(output, training=is_training)
if index != counts_layer:
output = tf.nn.relu(output)
else:
output = tf.nn.sigmoid(output)
index = index + 1
vars_list = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, 'generator')
return output, vars_list
2.4.3 判别器(Discriminator)
def discriminator(samples, depth_list = [128, 1], is_training = True, is_reuse = False):
output = tf.convert_to_tensor(samples, tf.float32)
with tf.variable_scope('discriminator', reuse=is_reuse):
index = 1
counts_layer = len(depth_list)
for depth in depth_list:
in_dim = output.get_shape()[1].value
xavier_stddev = xavier_init(in_dim)
output = tf.layers.dense(output, depth, kernel_initializer=tf.random_normal_initializer(mean=0, stddev=xavier_stddev))
output = tf.layers.batch_normalization(output, training=is_training)
if index != counts_layer:
output = tf.nn.relu(output)
else:
output = tf.nn.sigmoid(output)
index = index + 1
vars_list = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, 'discriminator')
return output, vars_list
2.4.4 损失函数
#loss
samples_real = X
samples_fake, G_vars_list = generator(Z, [128, 784], is_training, False)
prob_real, D_vars_list = discriminator(samples_real, [128, 1], is_training, False)
prob_fake, D_vars_list = discriminator(samples_fake, [128, 1], is_training, True)
loss_real = tf.reduce_mean(tf.log(prob_real + TINY))
loss_fake = tf.reduce_mean(tf.log(1-prob_fake + TINY))
loss_D = -(loss_real + loss_fake)
loss_G = -tf.reduce_mean(tf.log(prob_fake + TINY))
#solver
solver_D = tf.train.AdamOptimizer().minimize(loss_D, var_list=D_vars_list)
solver_G = tf.train.AdamOptimizer().minimize(loss_G, var_list=G_vars_list)
2.4.5 优化
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for iter in range(999999):
samples_batch, _ = MNIST.train.next_batch(batch_size)
noise = Z_sample([batch_size, dim_Z])
_, loss_D_curr = sess.run([solver_D, loss_D], feed_dict={X: samples_batch, Z: noise, is_training:True})
_, loss_G_curr = sess.run([solver_G, loss_G], feed_dict={Z: noise, is_training: True})
if iter%1000 == 0:
print('Iter:', iter, 'Loss_D:', loss_D_curr, 'Loss_G:', loss_G_curr)
samples_show = sess.run(samples_fake, feed_dict={Z: Z_sample([2048, dim_Z]), is_training: False})
2.4.6 结果
迭代0次
迭代1k次
迭代100k次
2.4 参考文献
- https://zh.wikipedia.org/wiki/%E5%9B%9A%E5%BE%92%E5%9B%B0%E5%A2%83
- 统计学习方法, 李航
- Generative Adversarial Nets, Ian J. Goodfellow
三、生成对抗网络的衍生模型
3.1 基于理论、结构和优化方法改进的衍生模型
3.1.1 基于理论创新的衍生模型
-
WGAN 以及 Improved WGAN
- WGAN模型优势:
- WGAN从理论上彻底解决GAN训练不稳定的问题,不再需要小心平衡生成器和判别器的训练程度。
作者还做了如下实验,当均基于DCGAN框架的时候,WGAN和DCGAN均可以生成质量良好的图片;但是当去掉生成器的
Batch Normalization层的时候,DCGAN无法生成图片,而WGAN仍然可以生成质量几乎无差别的图像;而当生成器使用多层感知机(MLP)模型的时候,DCGAN同样直接崩掉,而WGAN仍然可以较好的图像。- 基本解决的模式崩塌(collapse mode)的问题,确保了生成样本的多样性。
其实作者并没有理论证明模式崩塌问题的解决,只不过在所有的试验中均没有观察到该现象的出现,所以经验性的得出了“解决模式崩塌”的结论。 - 训练过程中有一个像交叉熵、准确率一样的数值来指示训练过程,这个数值越小表示训练的越好,生成器产生的图像质量越高。
如下图所示,随着分数的逐渐降低,生成的图像质量也越来越好。
- 不需要精心设计网络架构,最简单的多层全连接网络就可以实现
-
WGAN 实现方法:
- 判别器最后一层去掉sigmoid
- 生成器和判别器的损失函数不取log
- 每次更新判别器的参数之后把他们的绝对值截断到不超过固定常数c
- 不要基于动量算法(包括Momentum和Adam), 推荐使用RMSProp,SGD也可以
- 每训练n次判别器,训练一次生成器,论文中n取5
WGAN算法的伪代码如下图所示
-
Improved WGAN 实现方法:
- 在WGAN的基础上,将第3条限制取消,取而代之的是将梯度信息作为约束项加入到损失函数中
-
参考文献
- Arjovsky, M., et al. (2017). "Wasserstein gan." arXiv preprint arXiv:1701.07875.
- 令人拍案叫绝的Wasserstein GAN
3.1.2 基于结构改进的衍生模型
-
Deep Convolutional GAN (DCGAN)
结构设计:
- 使用 滑动卷积(strided convolutions) 和 反卷积(fractional-strided convolutions)去替代所有的pooling层。
- 在生成器和判别器中均使用批正则化方法(batch normalization),其中生成器的输出层和判别器的输入层使用批正则化方法。
- 去掉深层结构中的全连接隐藏层。
- 在生成器中,对输出层使用Tanh激活函数,对其他所有层使用ReLU激活函数。
- 在判别器中,对于输出层使用sigmoid激活函数,其他所有层使用LeakyReLU激活函数。
参数选择:
- 将输入数据预处理到区间[-1, 1]
- LeakyReLU中,slope of the leak 设置为0.2(也就是x<0部分的的斜率为0.2)
- 使用 均值为0,方差为0.02的正态分布去初始化网络权重
- 使用小批量随机梯度下降法(mini-batch stochastic gradient descent)方法训练网络,mini-batch size选择为128;优化器采用 Adam Optimizer优化方法,学习率为0.0002, 动量为0.5
3.2 基于应用的衍生模型
3.2.1 计算机视觉
3.2.1.1 图像特征提取
- 条件对抗生成网络(Conditional Generative Adversarial Network)
- 主要思想
原始GAN 提出,与其他生成式模型相比,GAN这种竞争的方式不再要求一个假设的数据分布,即不需要formulate p(x),而是使用一种分布直接进行采样,从而真正达到理论上可以完全逼近真实数据,这也是GAN最大的优势。然而,这种不需要预先建模的方法缺点是太过自由了,对于较大的图片,较多的 pixel的情形,基于简单 GAN 的方式就不太可控了。为了解决GAN太过自由这个问题,一个很自然的想法是给GAN加一些约束,于是便有了Conditional Generative Adversarial Nets(CGAN)【Mirza M, Osindero S. Conditional。
这项工作提出了一种带条件约束的GAN,在生成模型D 和判别模型G 的建模中均引入条件变量y,使用额外信息y对模型增加条件,可以指导数据生成过程。这些条件变量y可以基于多种信息,例如类别标签,用于图像修复的部分数据[2],来自不同模态(modality)的数据。如果条件变量y是类别标签,可以看做CGAN 是把纯无监督的 GAN 变成有监督的模型的一种改进。这个简单直接的改进被证明非常有效,并广泛用于后续的相关工作中[3,4]。Mehdi Mirza et al. 的工作是在MNIST数据集上以类别标签为条件变量,生成指定类别的图像。作者还探索了CGAN在用于图像自动标注的多模态学习上的应用,在MIR Flickr25000数据集上,以图像特征为条件变量,生成该图像的tag的词向量。
- 结构框架
相较于传统的GAN,CGAN在生成器和判别器的输入中均加入了条件变量
- 参考文献
Mirza M, Osindero S. Conditional Generative Adversarial Nets[J]. Computer Science, 2014:2672-2680.
3.2.1.2 图像到图像的转换
- 循环对抗生成网络(CycleGAN)
- 实现功能
CycleGAN主要实现了基于数据集,而不是数据对的图片到图片的转换。所以基于数据集,就是给定两种不同风格的数据集,而不需要指定图片之间的对应关系。如下图琐事,作者实现了图片风格的转换,斑马和马的转换,季节的转换等

- 结构框架
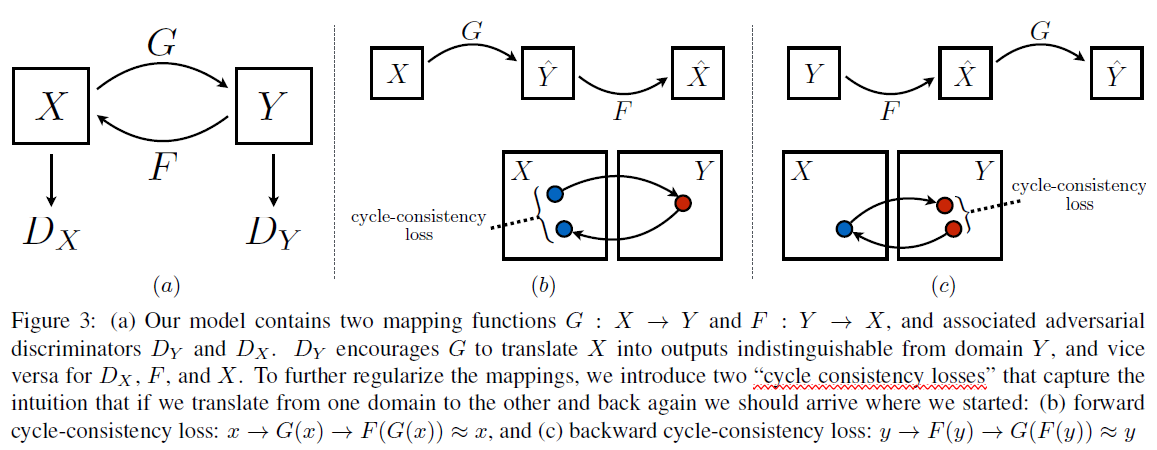
- 目标函数
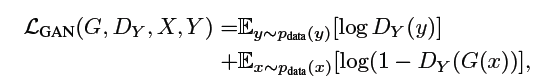
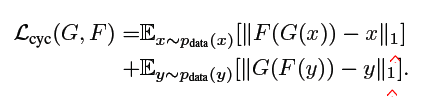
- 实验结果

五、生成对抗网络训练技巧
- 将输入归一化
- 将输入图片归一化到
[-1, 1]区间 - 使用
tanh作为生成器输出层的激活函数
- 将输入图片归一化到
- 修改损失函数
- 在 Goodfellow 的论文中,生成器
G的损失函数为min log(1-D(x)),由于该种损失函数容易导致梯度过早的消失,所以在实际中一般使用max log(D(x)) - 在训练生成器的时候
- 在 Goodfellow 的论文中,生成器
- 随机噪声采样分布
- 不要从均匀分布(uniform distribution)采集随机噪声z,应高从高斯分布(gaussian distribution)采集随机噪声z
- 批正则化(Batch Normalization)
- 对于真实样本和生成样本,构建不同的 mini batch, 例如对于一个 mini batch 中,全部都是真实样本,或者全部都是生成样本
- 当 Batch Normalization 不适用于模型的时候,可以采用 instance normalization,比如对于样本减去均值后再除以标准差,用公式表示就是
samples = (samples - mean(samples)) / stddev(samples)(???什么时候BN是不可用的)
-
避免稀疏梯度
- 梯度稀疏将会导致生成对抗不稳定,相比Relu、MaxOut,LeakyReLu将会产生更好的效果(??? 为什么梯度稀疏将会导致不稳定)
- 对于上采样,尽量使用滑动卷积(Convolution+Stride),Average Pooling也可以;对于下采样,尽量使用滑动反卷积(Deconvolution+Stride),或者PixelShuffle(???什么是pixelshuffle)
-
使用平滑的、带有噪声的标签
- 平滑标签:比如将正样本的标签1放松成0.7或者1.3, 将负样本的标签0放松成0.3 (???放松成多少)
- 噪声标签:在训练判别器的时候,使一些标签带有噪声,比如将正负样本标签反转,对于某些正样本将标签翻转为0/0.3,对于某些负样本将标签翻转为1/0.7/1.3 (???翻转比例应该是多少)
-
DCGAN、WGAN
- 当模型可以使用DCGAN框架的时候,尽量使用DCGAN框架。DCGAN虽然对模型的实现有诸多约束,但是DCGAN框架到目前为止在稳定性、收敛速度、生成图片质量方面都是比较好的框架
- 当DCGAN框架不可用的时候,比如模型无法使用 Batch Normalization ,可以考虑 WGAN 或者 Improved WGAN,这两个框架对于模型要求更少,但是在收敛速度和生成质量方面,想对于DCGAN的要差一些
-
参考文献
- 本文只列举出了笔者尝试过的,并且认为比较有效的一些方法和技巧;笔者认为,DCGAN、WGAN 以及 Improved WGAN 框架能够满足大部分的生成对抗网络模型
- How to Train a GAN? Tips and tricks to make GANs work
六、生成对抗网络其他资源
6.1 相关学者
-
Ian J. Goodfellow
简介: 机器学习、深度学习领域专家,就职于谷歌大脑(Google Brain),首次提出对生成对抗网络框架
6.2 主流会议
-
NIPS: Conference and Workshop on Neural Information Processing Systems
中国及学籍学会推荐国际学术会议,人工智能领域A类会议,主要收录包括机器学习以及计算神经科学等在内的文章,首篇生成对抗网络文章就发表在这个会议上。
-
ICLR: International Conference on Learning Representations
ICLR创办于2013年,虽然相较于人工智能其他领域的老牌会议还非常年轻,但已然成为深度学习领域的顶级会议。ICLR由深度学习三大巨头之二 Toshua Bengio 和 Yann LeCun牵头创办。ICLR最大的亮点是不仅仅是大牛创办,更是由于他Open Review 的评审机制。在这种评审机制下,所有论文都会公开姓名等信息,并且接受所有同行的评价和提问,任何学者都可以实名或者匿名的评价论文,而且在公开评审结束后,论文作者也能够对论文进行调整和修改。多篇对抗生成网络均有发表在这个会议上,比如被目前很多GAN方所基于的DCGAN
6.3 其他资源
-
生成对抗网络论文总结
- 该工程托管在
Github上,由托管作者不定期维护,并且持续更新,该工程为大家提供了一个方便的途径去了解GAN的最新进展 - A list of papers on Generative Adversarial (Neural) Networks
- 该工程托管在
-
生成对抗网络代码示例
- 该工程托管在
Github上,收集了打两个各种GAN、VAE以及他们的衍生模型的简单代码实现,代码简洁已读,适合初学者学习使用。每种模型均包含Tensorflow和Pytorch的实现。 - Collection of generative models, e.g. GAN, VAE in Pytorch and Tensorflow
- 该工程托管在
未完待续
关注我们的公众号,获取最新关于专知以及人工智能的资讯、技术、算法、深度干货等内容。扫一扫下方关注我们的微信公众号。