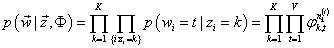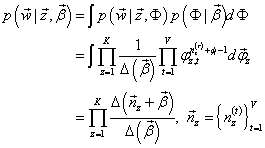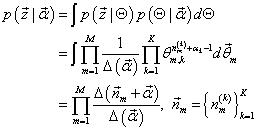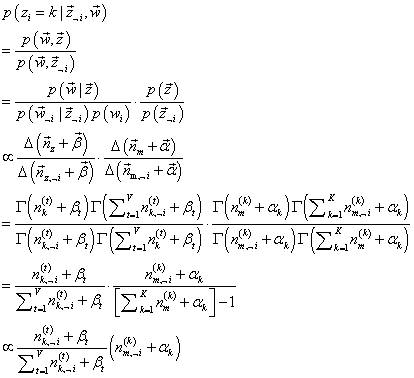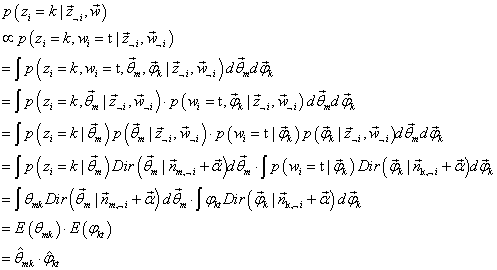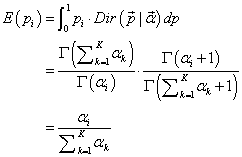会员服务

3、Gibbs采样

专知出品

3、Gibbs采样

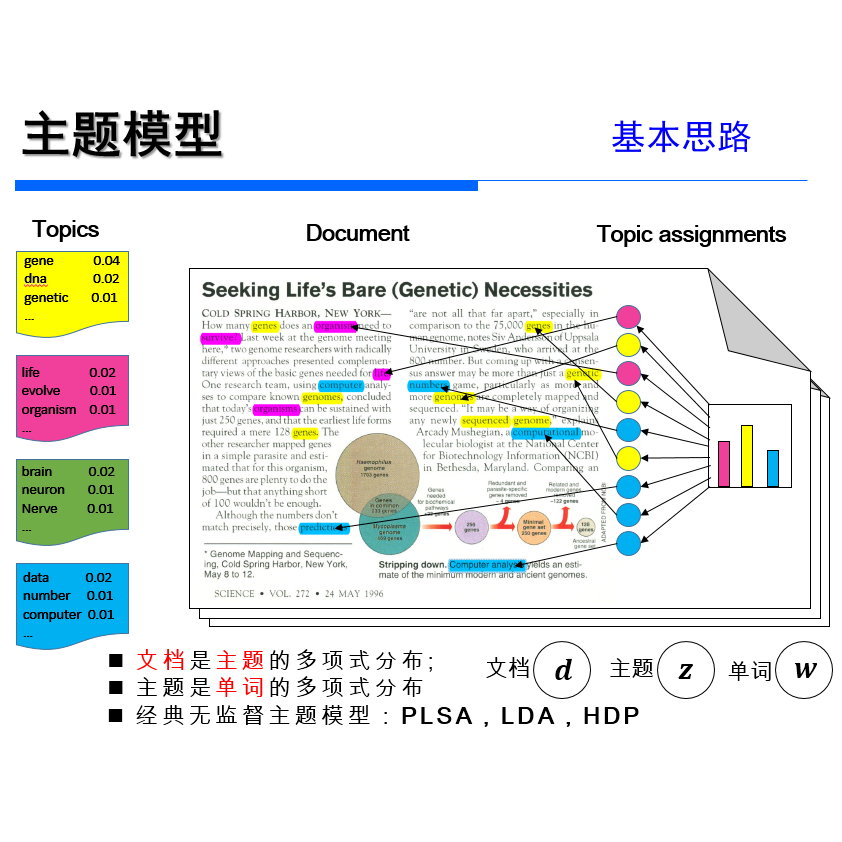
Blei的LDA原始论文（Latent Dirichlet
Allocation）中给出隐变量的后验分布如下图，核心问题是给出一篇文档，如何推断隐变量：

p ( θ , z ∣ w , α , β ) = p ( θ , z , w ∣ α , β ) p ( w ∣ α , β ) p\left( {\theta ,z|w,\alpha ,\beta } \right) = {{p\left( {\theta ,z,w|\alpha ,\beta } \right)} \over {p\left( {w|\alpha ,\beta } \right)}}

其中，由于文档生成过程可写为：

p ( θ , z , w ∣ α , β ) = p ( θ ∣ α ) ∏ n = 1 N p ( z n ∣ θ ) p ( w n ∣ z n , β ) p\left( {\theta ,z,w|\alpha ,\beta } \right) = p\left( {\theta |\alpha } \right)\prod\limits_{n = 1}^N {p\left( {{z_n}|\theta } \right)p\left( {{w_n}|{z_n},\beta } \right)}

对隐变量积分可得：

p ( w ∣ α , β ) = Γ ( ∑ i α i ) ∏ i Γ ( α i ) ∫ ( ∏ i = 1 k θ i α i − 1 ) ( ∏ n = 1 N ∑ i = 1 k ∏ j = 1 V ( θ i β i j ) w n j ) d θ p\left( {w|\alpha ,\beta } \right) = {{\Gamma \left( {\sum\nolimits_i {{\alpha _i}} } \right)} \over {\prod\nolimits_i {\Gamma \left( {{\alpha _i}} \right)} }}\int {\left( {\prod\limits_{i = 1}^k {\theta _i^{{\alpha _i} - 1}} } \right)\left( {\prod\limits_{n = 1}^N {\sum\limits_{i = 1}^k {\prod\limits_{j = 1}^V {{{\left( {{\theta _i}{\beta _{ij}}} \right)}^{w_n^j}}} } } } \right)d\theta }

由于 θ \theta 和 β \beta 之间的耦合，导致上述隐变量的推断通常是难以直接计算的，因此引入各种近似计算方法，比如变分法和Gibbs Sampling方法。

类似于PLSA，LDA的原始论文中是用的变分+EM算法估计未知参数，后来发现另一种估计LDA未知参数的方法更直观，更容易理解，这种方法就是：Gibbs Sampling，有时叫Gibbs采样或Gibbs抽样，都一个意思。Gibbs抽样是马尔可夫链蒙特卡尔理论（MCMC）中用来获取一系列近似等于指定多维概率分布（比如2个或者多个随机变量的联合概率分布）观察样本的算法。

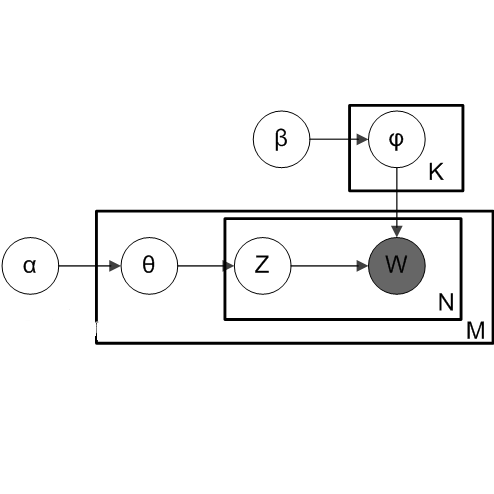
OK，给定一个文档集合，w是可以观察到的已知变量， α \alpha 和 β \beta 是根据经验给定的先验参数，其他的变量z，θ和φ都是未知的隐含变量，需要根据观察到的变量来学习估计的。根据LDA的图模型，可以写出所有变量的联合分布：

p ( w ⃗ m , z ⃗ m , θ ⃗ m , Φ ∣ α ⃗ , β ⃗ ) = ∏ n = 1 N m p ( w m , n ∣ φ ⃗ z m , n ) p ( z m , n ∣ θ ⃗ m ) ⋅ p ( θ ⃗ m ∣ α ⃗ ) ⋅ p ( Φ ∣ β ⃗ ) p\left( {{{\vec w}_m},{{\vec z}_m},{{\vec \theta }_m},\Phi |\vec \alpha ,\vec \beta } \right) = \prod\limits_{n = 1}^{{N_m}} {p\left( {{w_{m,n}}|{{\vec \varphi }_{{z_{m,n}}}}} \right)p\left( {{z_{m,n}}|{{\vec \theta }_m}} \right) \cdot p\left( {{{\vec \theta }_m}|\vec \alpha } \right) \cdot p\left( {\Phi |\vec \beta } \right)}

注：上述公式中及下文中， z m , n {z_{m,n}} 等价上文中定义的 z i , j {z_{i,j}} ， w m , n {w_{m,n}} 等价于上文中定义的 w i , j {w_{i,j}} ， φ ⃗ z m , n {\vec \varphi _{{z_{m,n}}}} 等价于上文中定义的 ϕ z i , j {\phi _{{z_{i,j}}}} ， θ m {\theta _m} 等价于上文中定义的 θ i {\theta _i} 。

因为 α \alpha 是文档-主题分布的狄利克雷先验参数，文档-主题分布 Θ \Theta 确定具体主题，且 β \beta 是主题-词分布的狄利克雷先验参数、主题-词分布 Φ \Phi 确定具体词。对上式进行积分，在Collapsed LDA Gibbs sampler中（参照Parameter estimation for text analysis_Gibbs sampling）。将 z m , n {z_{m,n}} 视为隐变量（视为马尔科夫链的状态变量）， w i , j {w_{i,j}} 为观测值，将参数 Θ \Theta 和 Φ \Phi 解释为观测值和隐变量的统计量。将其中的参数 Θ \Theta 和 Φ \Phi 整合，即把这两个变量积分掉了，从而简化联合分布的写法，这种方法被称为“collapsed”。所以上述式子等价于下述式子所表达的联合概率分布：

p ( w ⃗ m , z ⃗ m , θ ⃗ m , Φ ∣ α ⃗ , β ⃗ ) = ∏ n = 1 N m p ( w m , n ∣ φ ⃗ z m , n ) p ( z m , n ∣ θ ⃗ m ) ⋅ p ( θ ⃗ m ∣ α ⃗ ) ⋅ p ( Φ ∣ β ⃗ ) p\left( {{{\vec w}_m},{{\vec z}_m},{{\vec \theta }_m},\Phi |\vec \alpha ,\vec \beta } \right) = \prod\limits_{n = 1}^{{N_m}} {p\left( {{w_{m,n}}|{{\vec \varphi }_{{z_{m,n}}}}} \right)p\left( {{z_{m,n}}|{{\vec \theta }_m}} \right) \cdot p\left( {{{\vec \theta }_m}|\vec \alpha } \right) \cdot p\left( {\Phi |\vec \beta } \right)}

其中，第一项因子 p ( w ⃗ ∣ z ⃗ , β ⃗ ) p\left( {\vec w|\vec z,\vec \beta } \right) 表示的是根据确定的主题 z ⃗ \vec z 和主题-词分布的先验分布参数 β \beta 采样词的过程，第二项因子 p ( z ⃗ ∣ α ⃗ ) p\left( {\vec z|\vec \alpha } \right) 是根据文档-主题分布的先验分布参数 α \alpha 采样主题的过程，这两项因子是需要计算的两个未知参数。

由于这两个过程是独立的，所以下面可以分别处理，各个击破。

第一个因子 p ( w ⃗ ∣ z ⃗ , β ⃗ ) p\left( {\vec w|\vec z,\vec \beta } \right) ，可以根据确定的主题 z ⃗ \vec z 和从先验分布 β \beta 取样得到的主题-词分布 Φ \Phi 产生：

p ( w ⃗ ∣ z ⃗ , Φ ) = ∏ i = 1 W p ( w i ∣ z i ) = ∏ i = 1 W φ z i , w i p\left( {\vec w|\vec z,\Phi } \right) = \prod\limits_{i = 1}^W {p\left( {{w_i}|{z_i}} \right)} = \prod\limits_{i = 1}^W {{\varphi _{{z_i},{w_i}}}}

由于样本中的词服从参数为主题 z i z_i 的独立多项分布，这意味着可以把上面对词的乘积分解成分别对主题和对词的两层乘积：

图片

其中， n k ( t ) n_k^{\left( t \right)} 是词 t 在主题 k 中出现的次数。

回到第一个因子上来。目标分布 p ( w ⃗ ∣ z ⃗ , β ⃗ ) p\left( {\vec w|\vec z,\vec \beta } \right) 需要对主题-词分布Φ积分，且结合我们之前定义的Dirichlet分布的归一化系数 Δ ( α ⃗ ) \Delta \left( {\vec \alpha } \right) 的公式

Δ ( α ⃗ ) = ∫ ∏ k = 1 V p k α k − 1 d p ⃗ \Delta \left( {\vec \alpha } \right) = \int {\prod\limits_{k = 1}^V {p_k^{{\alpha _k} - 1}d\vec p} }

可得：

图片

这个结果可以看作K个Dirichlet-Multinomial模型的乘积。

现在开始求第二个因子 p ( z ⃗ ∣ α ⃗ ) p\left( {\vec z|\vec \alpha } \right) 。类似于 p ( w ⃗ ∣ z ⃗ , β ⃗ ) p\left( {\vec w|\vec z,\vec \beta } \right) 的步骤，先写出条件分布，然后分解成两部分的乘积：

p ( z ⃗ ∣ Θ ) = ∏ i = 1 W p ( z i ∣ d i ) = ∏ m = 1 M ∏ k = 1 K p ( z i = k ∣ d i = m ) = ∏ m = 1 M ∏ k = 1 K θ m , k n m ( k ) p\left( {\vec z|\Theta } \right) = \prod\limits_{i = 1}^W {p\left( {{z_i}|{d_i}} \right) = \prod\limits_{m = 1}^M {\prod\limits_{k = 1}^K {p\left( {{z_i} = k|{d_i} = m} \right)} } = \prod\limits_{m = 1}^M {\prod\limits_{k = 1}^K {\theta _{m,k}^{n_m^{\left( k \right)}}} } }

其中， d i {d_i} 表示的单词 i 所属的文档， n m ( t ) n_m^{\left( t \right)} 是主题 k 在文章 m 中出现的次数。

对文档-主题分布Θ积分可得：

图片

综合第一个因子和第二个因子的结果，得到 p ( w ⃗ , z ⃗ ) p\left( {\vec w,\vec z} \right) 的联合分布结果为：

p ( z ⃗ , w ⃗ ∣ α ⃗ , β ⃗ ) = ∏ z = 1 K Δ ( n ⃗ z + β ⃗ ) Δ ( β ⃗ ) ∏ m = 1 M Δ ( n ⃗ m + α ⃗ ) Δ ( α ⃗ ) p\left( {\vec z,\vec w|\vec \alpha ,\vec \beta } \right) = \prod\limits_{z = 1}^K {{{\Delta \left( {{{\vec n}_z} + \vec \beta } \right)} \over {\Delta \left( {\vec \beta } \right)}}} \prod\limits_{m = 1}^M {{{\Delta \left( {{{\vec n}_m} + \vec \alpha } \right)} \over {\Delta \left( {\vec \alpha } \right)}}}

接下来，有了联合分布 p ( w ⃗ , z ⃗ ) p\left( {\vec w,\vec z} \right) ，咱们便可以通过联合分布来计算在给定可观测变量 w下的隐变量z的条件分布（后验分布） p ( z ⃗ ∣ w ⃗ ) p\left( {\vec z|\vec w} \right) 来进行贝叶斯分析。

换言之，有了这个联合分布后，要求解第m篇文档中的第n个词（下标为 i = ( m , n ) i = \left( {m,n} \right) 的词）的全部条件概率就好求了。

先定义几个变量。 ¬ i \neg i 表示除去 i i 的词， w ⃗ = { w i = t , w ⃗ ¬ i } \vec w = \left\{ {{w_i} = t,{{\vec w}_{\neg i}}} \right\} ， z ⃗ = { z i = k , z ⃗ ¬ i } \vec z = \left\{ {{z_i} = k,{{\vec z}_{\neg i}}} \right\} 。然后，排除当前词的主题分配，即根据其他词的主题分配和观察到的单词来计算当前词主题的概率公式为：

图片

且有：

图片

最后一步，便是根据Markov链的状态 z i z_i 获取文档-主题分布的参数Θ和主题-词分布的参数Φ。

换言之根据贝叶斯法则和Dirichlet先验，以及上文中得到的 p ( w ⃗ ∣ z ⃗ , Φ ) p\left( {\vec w|\vec z,\Phi } \right) 和 p ( z ⃗ ∣ Φ ) p\left( {\vec z|\Phi } \right) 各自被分解成两部分乘积的结果，可以计算得到每个文档上Topic的后验分布和每个Topic下的词的后验分布分别如下（据上文可知：其后验分布跟它们的先验分布一样，也都是Dirichlet
分布）：

p ( φ ⃗ k ∣ z ⃗ m , α ⃗ ) = 1 Z φ k ∏ n = 1 N m p ( z m , n ∣ θ ⃗ m ) ⋅ p ( φ ⃗ k ∣ α ⃗ ) = D i r ( φ ⃗ k ∣ n ⃗ m + α ⃗ ) p\left( {{{\vec \varphi }_k}|{{\vec z}_m},\vec \alpha } \right) = {1 \over {{Z_{{\varphi _k}}}}}\prod\limits_{n = 1}^{{N_m}} {p\left( {{z_{m,n}}|{{\vec \theta }_m}} \right) \cdot p\left( {{{\vec \varphi }_k}|\vec \alpha } \right)} = Dir\left( {{{\vec \varphi }_k}|{{\vec n}_m} + \vec \alpha } \right)

p ( φ ⃗ k ∣ z ⃗ , w ⃗ , β ⃗ ) = 1 Z φ k ∏ { i : z i − k } p ( w i ∣ φ ⃗ k ) ⋅ p ( φ ⃗ k ∣ β ⃗ ) = D i r ( φ ⃗ k ∣ n ⃗ k + β ⃗ ) p\left( {{{\vec \varphi }_k}|\vec z,\vec w,\vec \beta } \right) = {1 \over {{Z_{{\varphi _k}}}}}\prod\limits_{\left\{ {i:{z_i} - k} \right\}} {p\left( {{w_i}|{{\vec \varphi }_k}} \right) \cdot p\left( {{{\vec \varphi }_k}|\vec \beta } \right)} = Dir\left( {{{\vec \varphi }_k}|{{\vec n}_k} + \vec \beta } \right)

其中， n ⃗ m {\vec n_m} 是构成文档m的主题数向量， n ⃗ k {\vec n_k} 是构成主题k的词项数向量。

此外，别忘了上文中所述的Dirichlet的一个性质，如下：

如果 p ⃗ ∼ D i r ( t ⃗ ∣ α ⃗ ) \vec p \sim Dir\left( {\vec t|\vec \alpha } \right) ，同样可以证明有下述结论成立：

E ( p i ) = ( α 1 ∑ i = 1 K α i , α 2 ∑ i = 1 K α i , . . . , α K ∑ i = 1 K α i ) E\left( {{p_i}} \right) = \left( {{{{\alpha _1}} \over {\sum\nolimits_{i = 1}^K {{\alpha _i}} }},{{{\alpha _2}} \over {\sum\nolimits_{i = 1}^K {{\alpha _i}} }},...,{{{\alpha _K}} \over {\sum\nolimits_{i = 1}^K {{\alpha _i}} }}} \right)

即：如果 p ⃗ ∼ D i r ( p ⃗ ∣ α ⃗ ) \vec p \sim Dir\left( {\vec p|\vec \alpha } \right) ，则 p ⃗ \vec p 中的任一元素的期望是：

图片

可以看出，超参数 α k {\alpha _k} 的直观意义就是事件先验的伪计数(prior pseudo-count)。所以，最终求解的两个Dirichlet 后验分布期望为：

θ m , k = n m ( k ) + α k ∑ k = 1 K n m ( k ) + α k {\theta _{m,k}} = {{n_m^{\left( k \right)} + {\alpha _k}} \over {\sum\nolimits_{k = 1}^K {n_m^{\left( k \right)} + {\alpha _k}} }}

φ k , t = n k ( t ) + β t ∑ t = 1 V n k ( t ) + β t {\varphi _{k,t}} = {{n_k^{\left( t \right)} + {\beta _t}} \over {\sum\nolimits_{t = 1}^V {n_k^{\left( t \right)} + {\beta _t}} }}

然后将 φ k , t {\varphi _{k,t}} 和 θ m , k {\theta _{m,k}} 的结果代入之前得到的 p ( z i = k ∣ z ⃗ ¬ i , w ⃗ ) ∝ p ( z i = k , w i = t ∣ z ⃗ ¬ i , w ⃗ ¬ i ) p\left( {{z_i} = k|{{\vec z}_{\neg i}},\vec w} \right) \propto p\left( {{z_i} = k,{w_i} = t|{{\vec z}_{\neg i}},{{\vec w}_{\neg i}}} \right) 的结果中，可得：

p ( z i = k ∣ z ⃗ ¬ i , w ⃗ ) ∝ n m , ¬ i ( k ) + α k ∑ k = 1 K n m , ¬ i ( k ) + α k ⋅ n k , ¬ i ( t ) + β t ∑ t = 1 V n k , ¬ i ( t ) + β t p\left( {{z_i} = k|{{\vec z}_{\neg i}},\vec w} \right) \propto {{n_{m,\neg i}^{\left( k \right)} + {\alpha _k}} \over {\sum\nolimits_{k = 1}^K {n_{m,\neg i}^{\left( k \right)} + {\alpha _k}} }} \cdot {{n_{k,\neg i}^{\left( t \right)} + {\beta _t}} \over {\sum\nolimits_{t = 1}^V {n_{k,\neg i}^{\left( t \right)} + {\beta _t}} }}

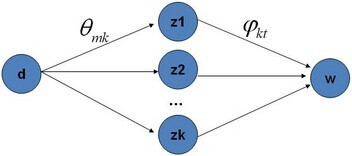
仔细观察上述结果，可以发现，式子的右半部分便是 p ( t o p i c ∣ d o c ) ⋅ p ( w o r d ∣ t o p i c ) p\left( {topic|doc} \right) \cdot p\left( {word|topic} \right) ，这个概率的值对应着 d o c → t o p i c → w o r d doc \to topic \to word 的路径概率。如此，K个topic 对应着K条路径，Gibbs Sampling 便在这K 条路径中进行采样，如下图所示：

图片

就这样，Gibbs Sampling通过求解出文档-主题分布和主题-词分布的后验分布，从而成功解决文档-主题分布和主题-词分布这两参数未知的问题。

参考文献

  1. http://www.arbylon.net/publications/text-est.pdf —《Parameter estimation for text analysis》

  2. rickjin的LDA数学八卦—http://vdisk.weibo.com/s/q0sGh/1360334108?utm_source=weibolife

  3. 马晨的LDA算法漫游指南—https://yuedu.baidu.com/ebook/d0b441a8ccbff121dd36839a.html

展开全文
相关主题
主题模型
LDA
Top
微信扫码咨询专知VIP会员
Top