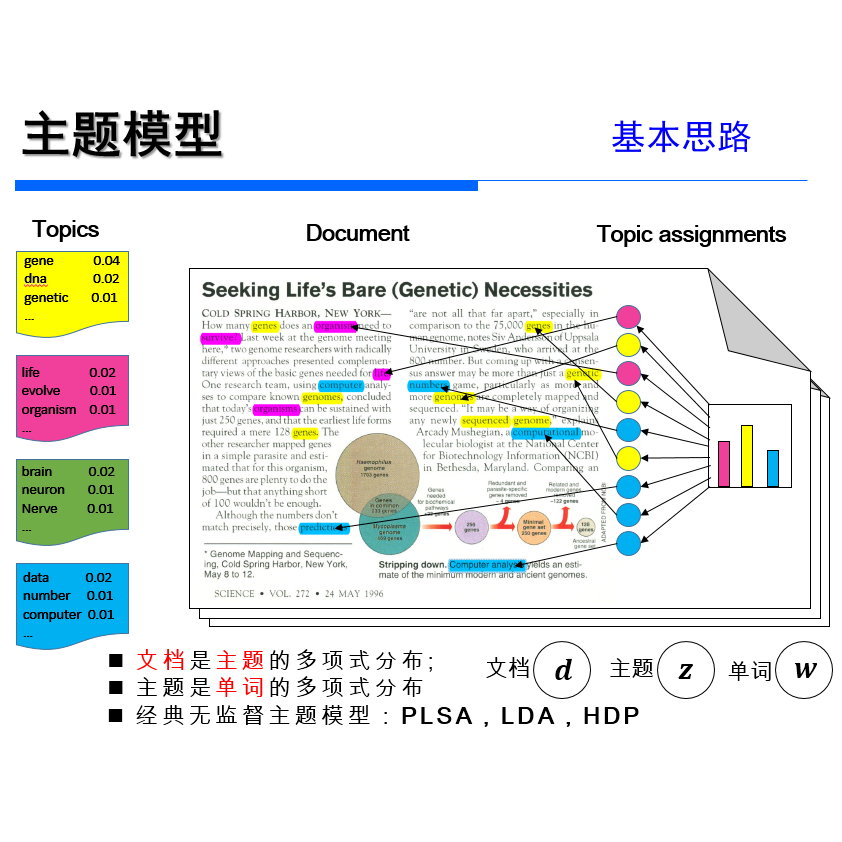
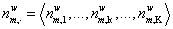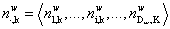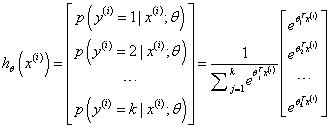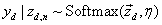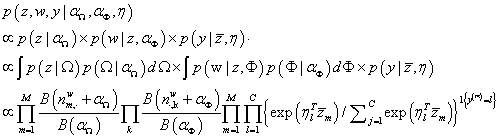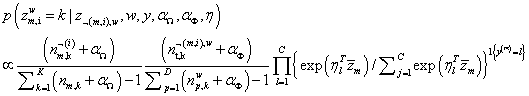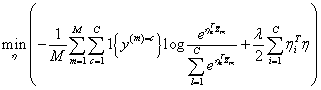会员服务

1、有监督主题模型（Supervised LDA, SLDA）

专知出品

1、SLDA

SLDA主题模型，主要思想是利用softmax分类器将文档类别标签信息，考虑到主题模型中，作为一个完整的模型进行训练，从而利用类别标签能很好的约束模型训练，能提高模型对于文本分类的分类性能。

Softmax分类器简介

**Logistic回归：**Logistic
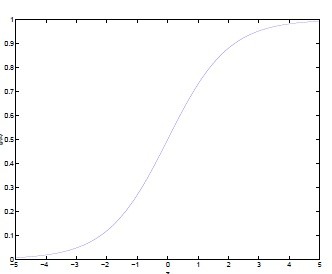
Regression虽然名字里带“回归”，但是它实际上是一种分类方法，用于两分类问题（即输出只有两种）。根据第二章中的步骤，需要先找到一个预测函数（h），显然，该函数的输出必须是两个值（分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

g ( z ) = 1 1 + e − z g\left( z \right) = {1 \over {1 + {e^{ - z}}}}

对应的函数图像是一个取值在0和1之间的S型曲线。

图片

Softmax回归

softmax回归是逻辑斯蒂回归的推广,即,逻辑斯蒂回归只能区分两个类,softmax回归将它推广到了k个，经常放在各种神经网络的最顶层当作分类器。

回想一下在 logistic回归中，我们的训练集由 m m 个已标记的样本构成 { ( x ( 1 ) , y ( 1 ) ) , . . . , ( x ( m ) , y ( m ) ) } \left\{ {\left( {{x^{\left( 1 \right)}},{y^{\left( 1 \right)}}} \right),...,\left( {{x^{\left( m \right)}},{y^{\left( m \right)}}} \right)} \right\} ：，其中输入特征 x ( i ) ∈ ℜ n + 1 {x^{\left( i \right)}} \in {\Re ^{n + 1}} 。（我们对符号的约定如下：特征向量 x x 的维度为 n + 1 n + 1 ，其中 x 0 = 1 {x_0} = 1 对应截距项） 由于 logistic 回归是针对二分类问题的，因此类标记 y ( i ) ∈ { 0 , 1 } {y^{\left( i \right)}} \in \left\{ {0,1} \right\} 。假设函数(hypothesis function) 如下：

h θ ( x ) = 1 1 + exp ( − θ T x ) {h_\theta }\left( x \right) = {1 \over {1 + \exp \left( { - {\theta ^T}x} \right)}}

我们训练模型参数$\theta $，使其能够最小化代价函数 ：

J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right) = - {1 \over m}\left[ {\sum\limits_{i = 1}^m {{y^{\left( i \right)}}\log {h_\theta }\left( {{x^{\left( i \right)}}} \right) + \left( {1 - {y^{\left( i \right)}}} \right)\log \left( {1 - {h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right)} } \right]

在 softmax回归中，我们解决的是多分类问题（相对于 logistic回归解决的二分类问题），类标 y y 可以取 k k 个不同的值（而不是2个）。因此，对于训练集 { ( x ( 1 ) , y ( 1 ) ) , . . . , ( x ( m ) , y ( m ) ) } \left\{ {\left( {{x^{\left( 1 \right)}},{y^{\left( 1 \right)}}} \right),...,\left( {{x^{\left( m \right)}},{y^{\left( m \right)}}} \right)} \right\} ，我们有 y ( i ) ∈ { 1 , 2 , . . . , k } {y^{\left( i \right)}} \in \left\{ {1,2,...,k} \right\} 。（注意此处的类别下标从1 开始，而不是 0）。例如，在 MNIST 数字识别任务中，我们有 k = 1 0 k = 10 个不同的类别。

对于给定的测试输入 x x ，我们想用假设函数针对每一个类别j估算出概率值 p ( y = j ∣ x ) p\left( {y = j|x} \right) 。也就是说，我们想估计 x x 的每一种分类结果出现的概率。因此，我们的假设函数将要输出一个 k k 维的向量（向量元素的和为1）来表示这 k k 个估计的概率值。
具体地说，我们的假设函数 h θ ( x ) {h_\theta }\left( x \right) 形式如下：

图片

其中 θ 1 , θ 2 , . . . , θ k ∈ ℜ n + 1 {\theta _1},{\theta _2},...,{\theta _k} \in {\Re ^{n + 1}} 是模型的参数。请注意 1 ∑ j = 1 k e θ j T x ( i ) {1 \over {\sum\nolimits_{j = 1}^k {{e^{\theta _j^T{x^{\left( i \right)}}}}} }} 这一项对概率分布进行归一化，使得所有概率之和为 1 。

详细内容请参考ufldl：

http://ufldl.stanford.edu/wiki/index.php/Softmax回归

SLDA（Supervised topic models）

SLDA（有监督主题模型）有很多扩展，包括Blei等人的“Supervised topic
models”，以及Labeled LDA，Disc LDA等。这里介绍一下Supervised topic
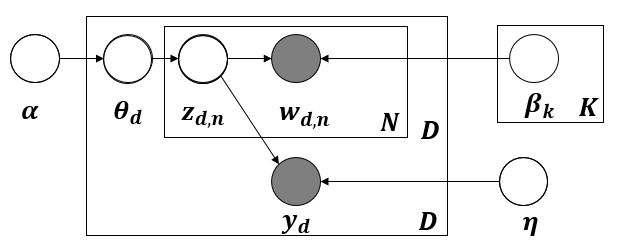
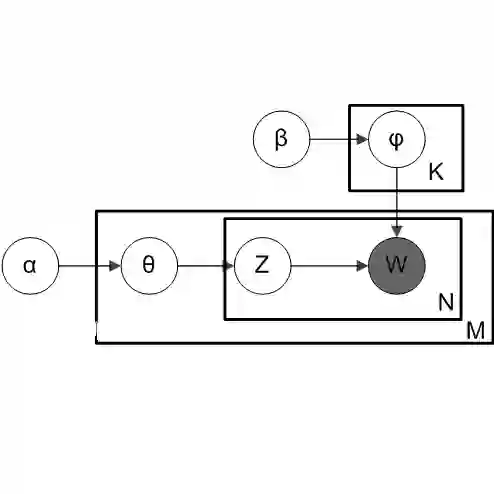
models，只介绍监督信息是离散的类标信息，开门见山，其图模型如下：

图片

SLDA图模型生成过程：

  • 对于每一个主题k：

  • 从Dirichlet分布中获取文档-主题分布 θ d : θ d ∣ α ∼ D i r ( α ) {\theta _d}:{\theta _d}|\alpha \sim Dir\left( \alpha \right) ；

  • 对于每个单词 w n {w_n} ：

  • 首先从文档-主题分布中获取一个主题： z n ∣ θ ∼ M u l t ( θ ) {z_n}|\theta \sim Mult\left( \theta \right) ；

  • 然后从对应的主题以及主题的主题-词分布中获取一个词： w n ∣ z n , β 1 : K ∼ M u l t ( β z n ) {w_n}|{z_n},{\beta _{1:K}} \sim Mult\left( {{\beta _{{z_n}}}} \right)

  • 获取单词类别标签： y ∣ z 1 : N , η ∼ N ( η T z ¯ ) y|{z_{1:N}},\eta \sim N\left( {{\eta ^T}\bar z} \right)

对于如何考虑单词的类别标签，作者在使用Softmax分类器，即：

图片

该模型的参数估计方法有多种，这里参考论文中“Multi-Modal Supervised Latent Dirichlet Allocation for Event Classification in Social Media”的方法，给出求解过程：

首先写出联合后验分布

图片

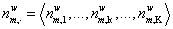其中 B ( α ) = ∏ k Γ ( α k ) Γ ( ∑ k α k ) B\left( \alpha \right) = {{\prod\nolimits_k {\Gamma \left( {{\alpha _k}} \right)} } \over {\Gamma \left( {\sum\nolimits_k {{\alpha _k}} } \right)}} 是归一化常数；图片是文档m中属于主题k的单词的数目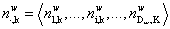；图片表示所有文档中，属于主题k的单词的数目；

利用EM算法求解未知变量，在E-step利用Gibbs Sampling采样变量z，根据给定的参数 η 1 : C {\eta _{1:C}} ，在M-step通过最大化联合似然更新参数 η 1 : C {\eta _{1:C}} （分类器）。

E-step：

利用collapsed Gibbs sampling采样当前词的topic，隐变量 z w {z^w} ，当前词分配主题k的概率公式为：

图片

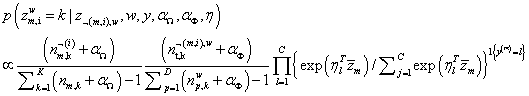
其中， z ¬ ( m , i ) , w {z_{\neg \left( {m,i} \right),w}} 表示文档-主题分布向量（除去当前位置i的词，只考虑文档m中其他维度的单词）。 ( n m , k ¬ ( i ) + α Ω ) ∑ k = 1 K ( n m , k + α Ω ) − 1 ( n t , k ¬ ( m , i ) , w + α Φ ) ∑ p = 1 D ( n p , k w + α Φ ) − 1 {{\left( {n_{m,k}^{\neg \left( i \right)} + {\alpha _\Omega }} \right)} \over {\sum\nolimits_{k = 1}^K {\left( {{n_{m,k}} + {\alpha _\Omega }} \right)} - 1}}{{\left( {n_{t,k}^{\neg \left( {m,i} \right),w} + {\alpha _\Phi }} \right)} \over {\sum\nolimits_{p = 1}^D {\left( {n_{p,k}^w + {\alpha _\Phi }} \right)} - 1}} 和传统的LDA类似，表示单词计数。 ∏ l = 1 C { exp ( η l T z ¯ m ) / ∑ j = 1 C exp ( η l T z ¯ m ) } 1 { y ( m ) = l } \prod\limits_{l = 1}^C {{{\left\{ {\exp \left( {\eta _l^T{{\bar z}_m}} \right)/\sum\nolimits_{j = 1}^C {\exp \left( {\eta _l^T{{\bar z}_m}} \right)} } \right\}}^{1\left\{ {{y^{\left( m \right)}} = l} \right\}}}} 考虑文档的类别信息，表示在当前分类器 η \eta 的条件下，当前词取主题k的概率。最终估计参数取值：

Φ k , t w = n t , k w + α Φ w ∑ p = 1 D w ( n p , k w + α Φ w ) \Phi _{k,t}^w = {{n_{t,k}^w + {\alpha _{{\Phi ^w}}}} \over {\sum\nolimits_{p = 1}^{{D_w}} {\left( {n_{p,k}^w + {\alpha _{{\Phi ^w}}}} \right)} }}

Ω m , k = n m , k + α Ω ∑ k = 1 K ( n m , k + α Ω ) {\Omega _{m,k}} = {{{n_{m,k}} + {\alpha _\Omega }} \over {\sum\nolimits_{k = 1}^K {\left( {{n_{m,k}} + {\alpha _\Omega }} \right)} }}

M-step：

通过最大化联合概率分布，更新分类参数 η \eta ，固定E-step获取的参数，相当于最大化 p ( y ∣ z ¯ , η ) p\left( {y|\bar z,\eta } \right) ，其中 z ¯ \bar z 是文档的表示。问题转化为下面的优化问题：

图片

参考文章

  1. sLDA—David M. Blei and Jon McAuliffe. Supervised topic models. In NIPS, 2007
展开全文
相关主题
主题模型
LDA
Top
微信扫码咨询专知VIP会员
Top