基于信息理论的机器学习-中科院自动化所胡包钢研究员教程分享02(附pdf下载)
点击上方“专知”关注获取专业AI知识!
【导读】上一次专知推出基于信息理论的机器学习报告,大家反响热烈,今天是胡老师提供的第二部分(为第三章内容)进行详细地注释说明,请大家查看!
▌概述
本次tutorial的目的是,1.介绍信息学习理论与模式识别的基本概念与原理;2.揭示最新的理论研究进展;3.从机器学习与人工智能的研究中启发思索。由于时间有限,本次只是大概介绍一下本次tutorial的内容,后续会详细介绍每一部分。
胡老师的报告内容分为三个部分:
引言(Introduction)
信息理论基础(Basics of Information Theory)
二值信道的理论进展(Theoretical Progress in Binary Channel)
分类评价中的信息度量(Information Measures in Classification Evaluation)
贝叶斯分类器和互信息分类器(Bayesian Classifiers and Mutual-information Classifiers)
总结和讨论(Summary and Discussions)
胡包钢研究员个人主页:
http://www.escience.cn/people/hubaogang/index.html
胡包钢老师简介:
胡包钢老师是机器学习与模式识别领域的知名学者,1993年在加拿大McMaster大学获哲学博士学位。1997年9月回国前在加拿大MemorialUniversity of Newfoundland, C-CORE研究中心担任高级研究工程师。目前为中国科学院自动化研究所研究员。2000-2005年任中法信息、自动化、应用数学联合实验室(LIAMA)中方主任。
▌PPT
第3章:二值信道的理论进展
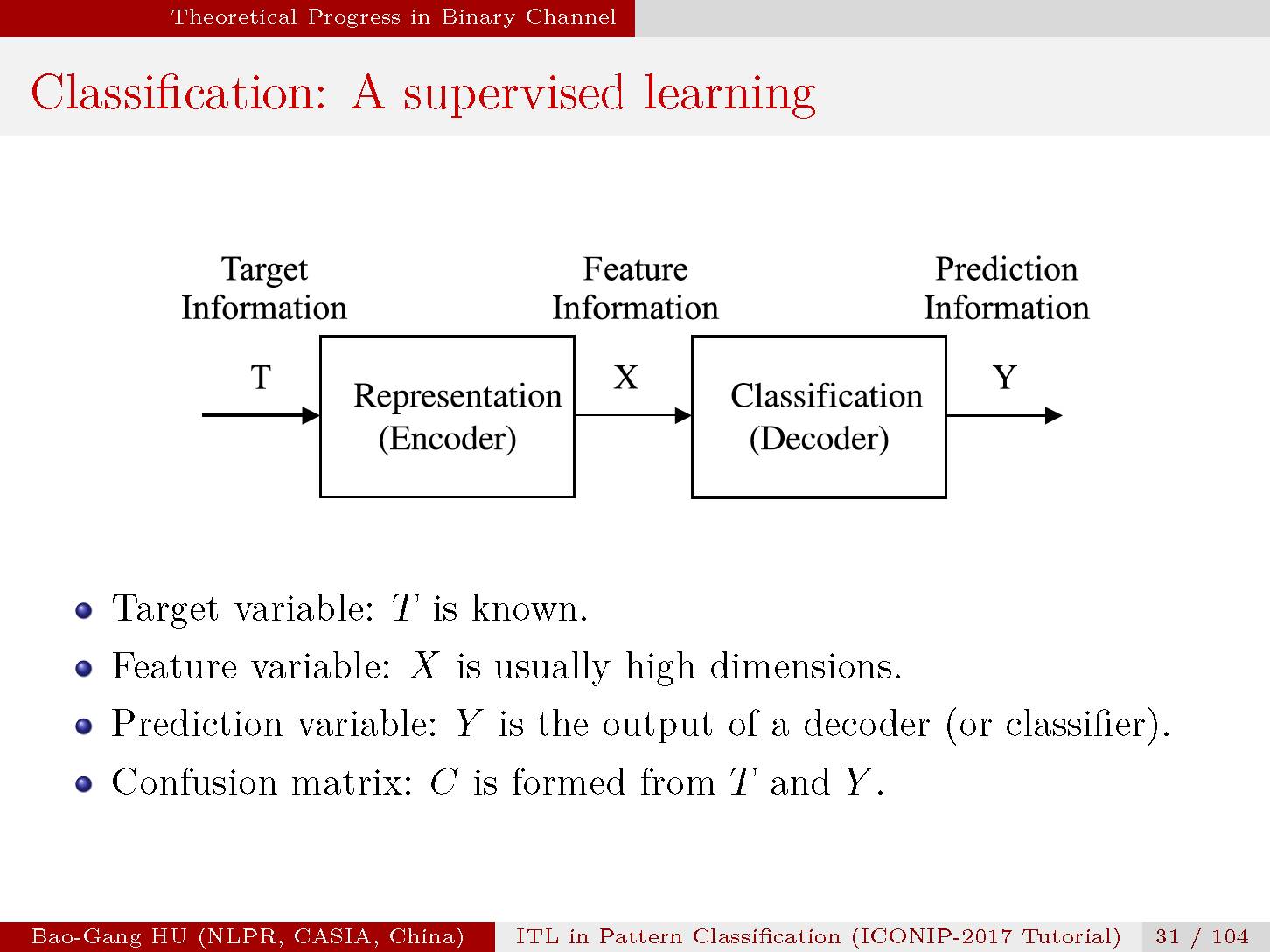
分类是一种监督学习,因为每个样本的目标类标T通常给出。
(目前的深度学习是“
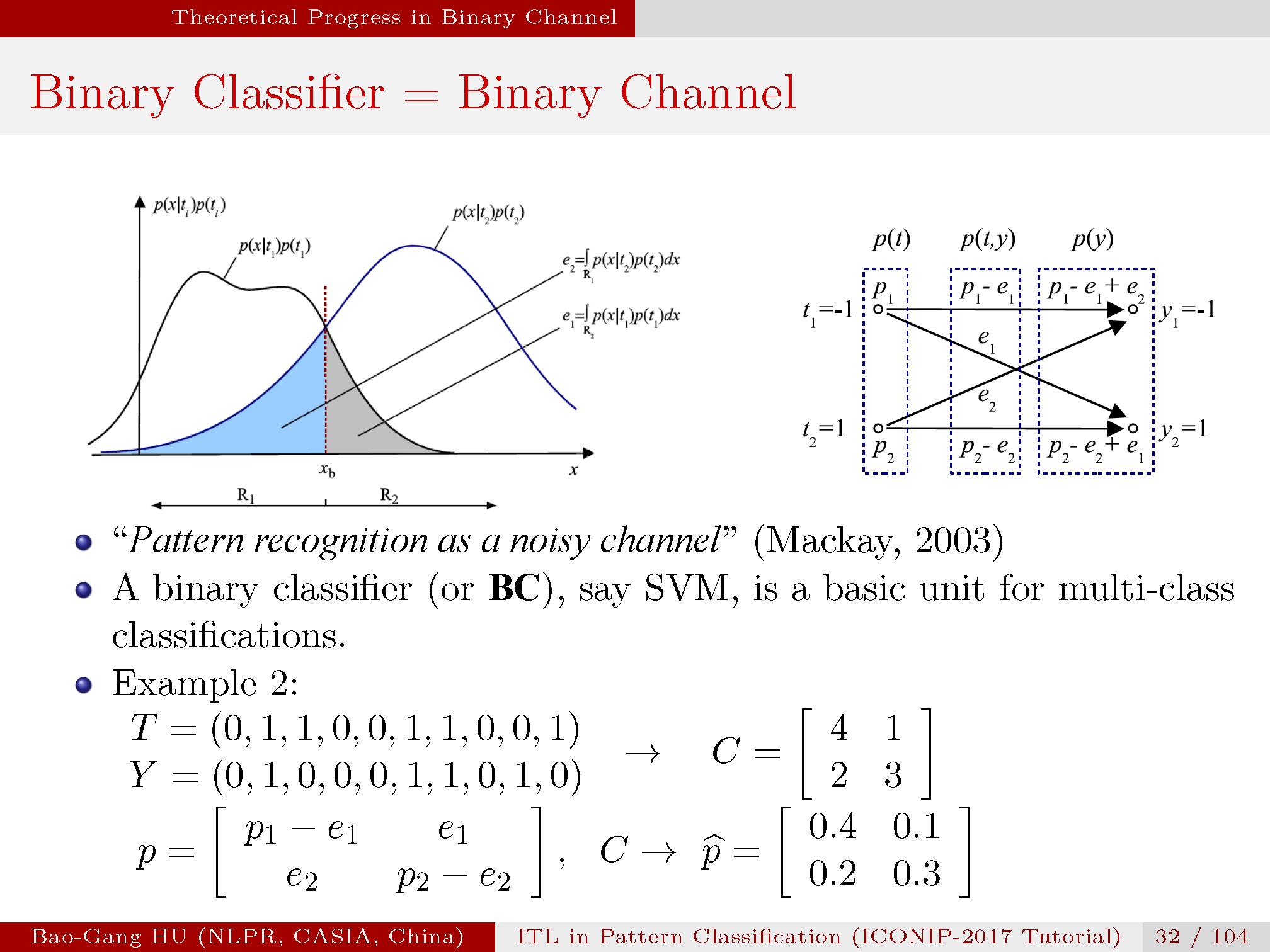
二值分类在通信理论中被称为二值信道。
在传统信息论研究中仅考虑贝叶斯误差。
信息论中已有的上界与下界计算公式。它们适用于m类有限类别,
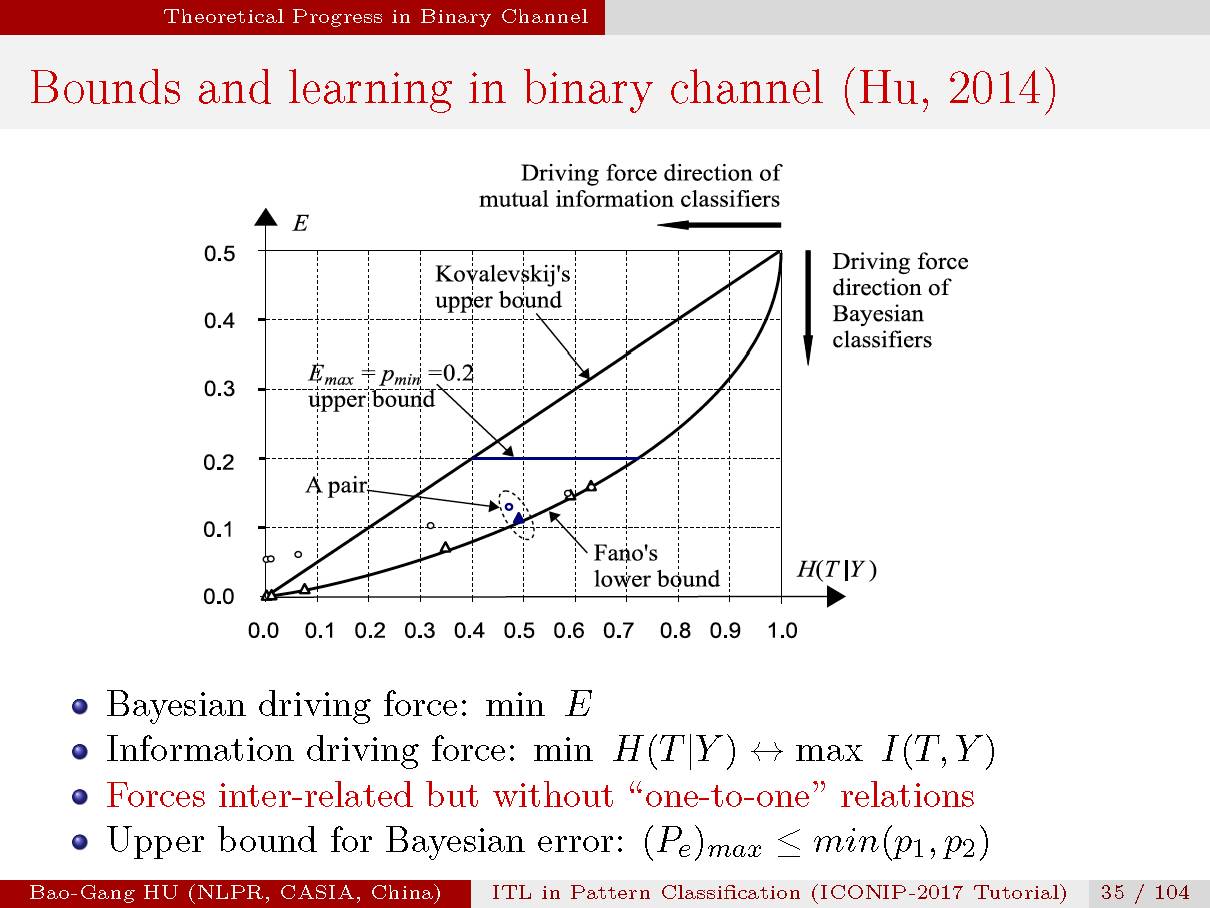
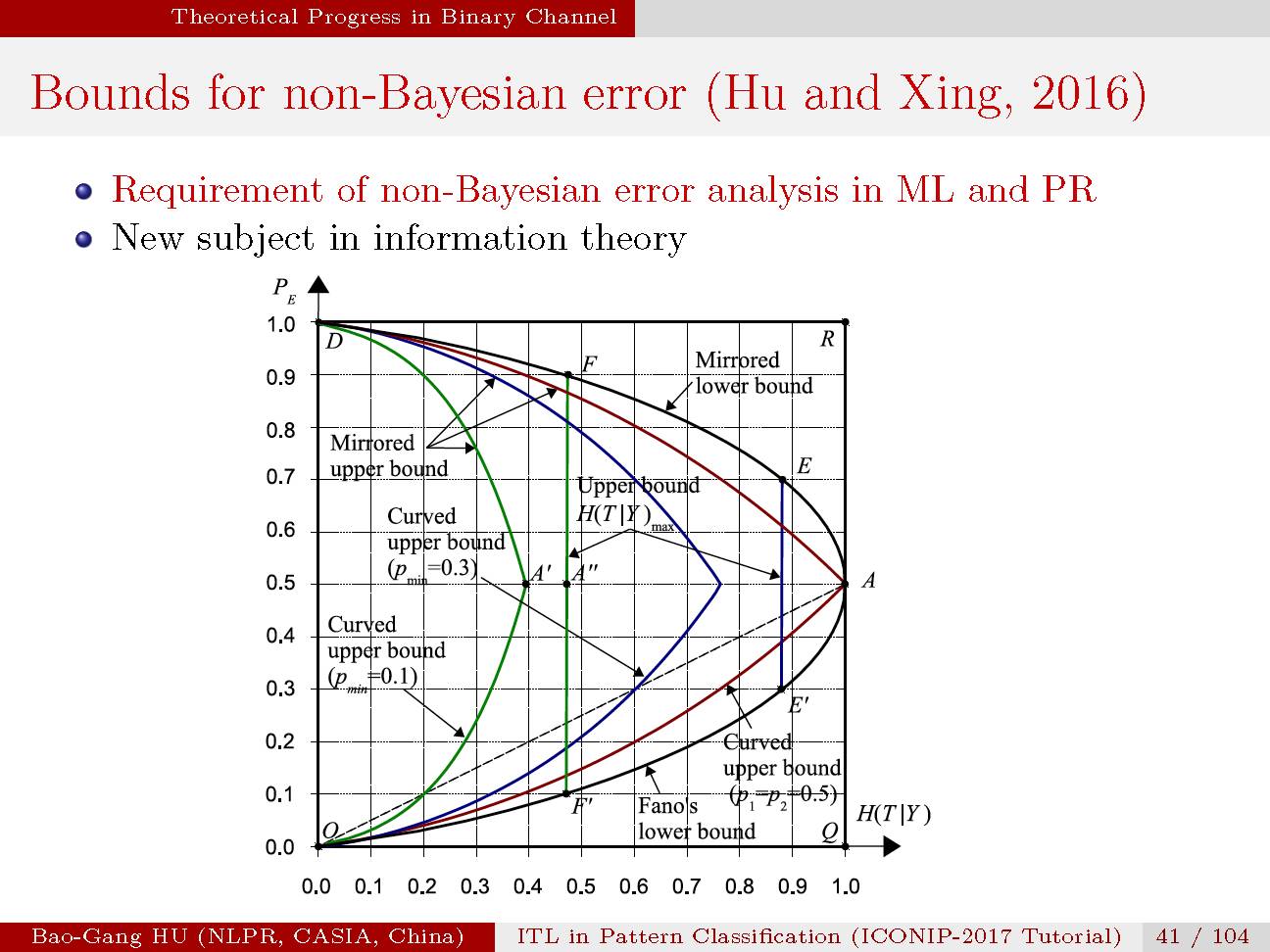
该图示意了二值分类上界与下界曲线。
二值分类中条件熵计算公式。由于H(T)通常为固定值,
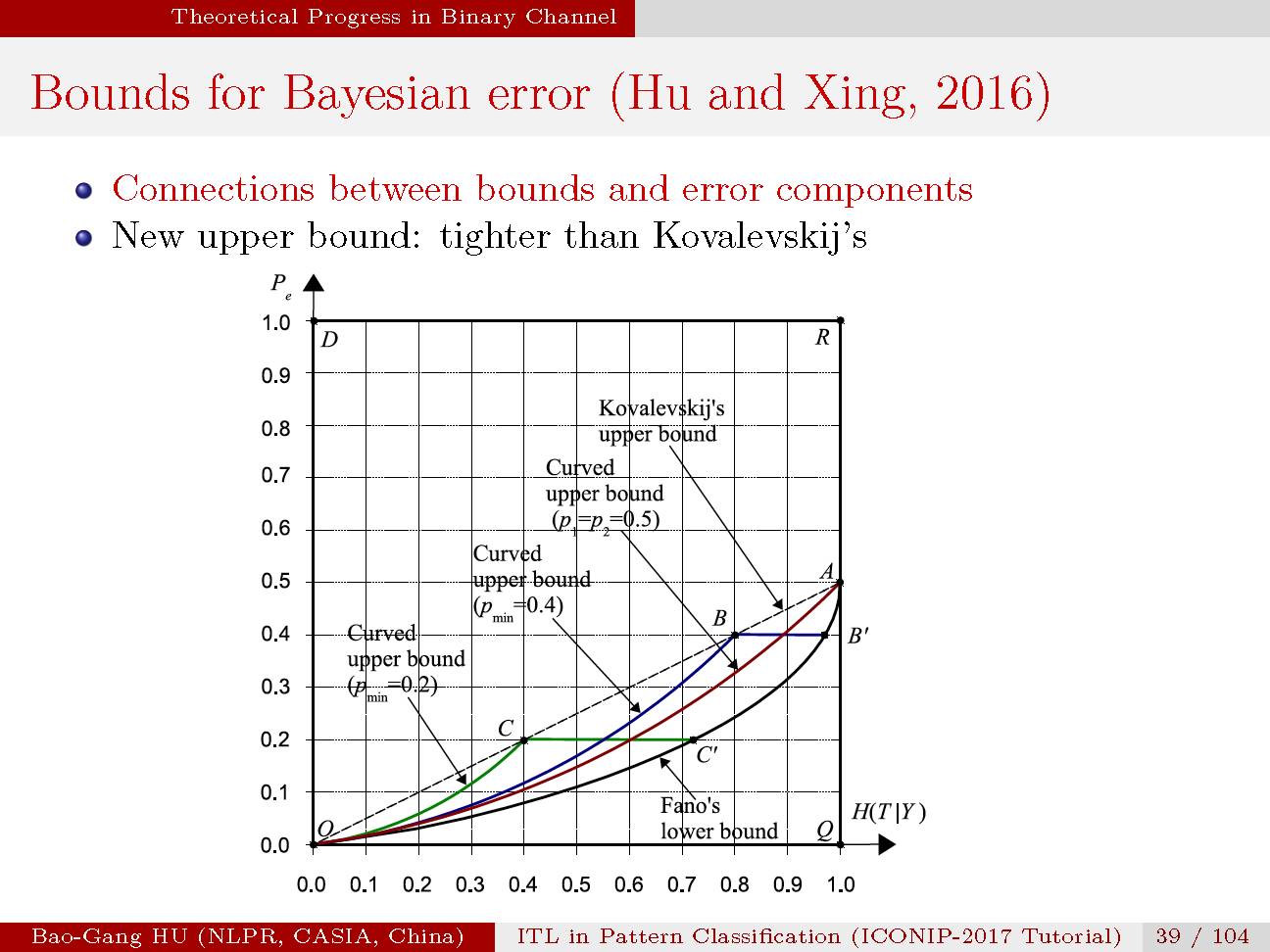
应用优化的方法我们从联合概率分布导出上下界计算公式,
贝叶斯误差与条件熵的关联关系。下界与Fano完全相同,
该界同时包括互信息为零(即条件熵最大,或
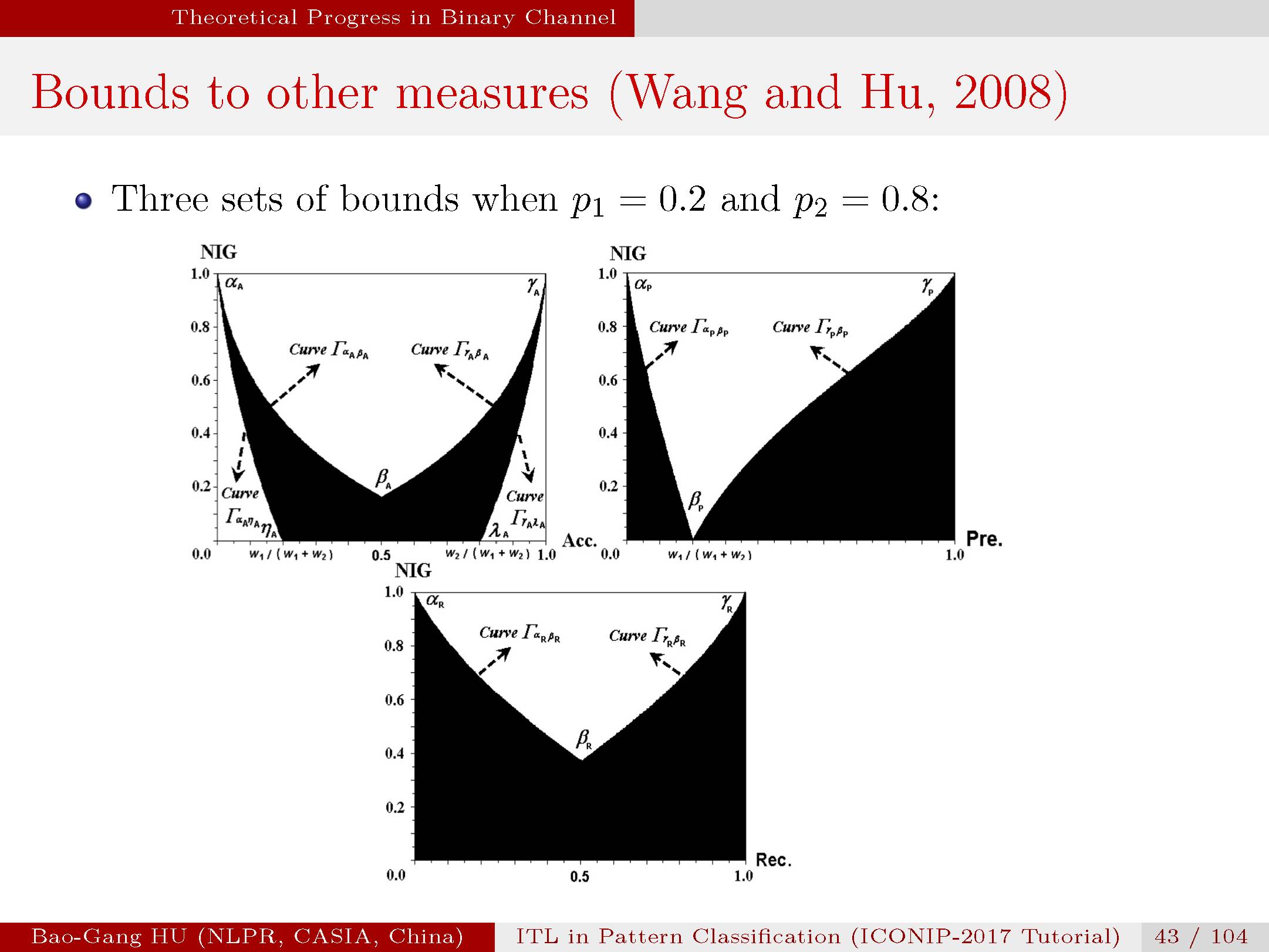
非贝叶斯误差与条件熵的关联关系。
这是首次推导的二值分类性能指标与互信息关联的关系式。
第3章总结
误差与条件熵的界分析是建立信息类学习目标与传统经验类学习目标
第三部分的二值信道的理论进展结束了,敬请期待下一期内容。
特别提示-信息论报告下载:
请关注专知公众号(扫一扫最下面专知二维码,或者点击上方蓝色专知),
后台回复“ITL” 就可以获取胡老师报告的pdf下载链接~
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域23个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请关注我们的公众号,获取人工智能的专业知识。扫一扫关注我们的微信公众号。
请加专知小助手微信(Rancho_Fang),加入专知主题人工智能群交流~
点击“阅读原文”,使用专知!