PyTorch-专知-链路化知识-5、< 快速理解系列 (四): 图文 代码, 让你快速理解 Dropout >
5、< 快速理解系列(四): 图文 代码, 让你快速理解Dropout >
Dropout
学过神经网络的童鞋应该知道神经网络很容易过拟合。而且,如果要用集成学习的思想去训练非常多个神经网络,集成起来抵制过拟合,这样开销非常大并且也不一定有效。于是,这群大神提出了Dropout方法:在神经网络训练时,随机把一些神经单元去除,“瘦身”后的神经网络继续训练,最后的模型,是保留所有神经单元,但是神经的连接权重w乘上了一个刚才随机去除指数p.
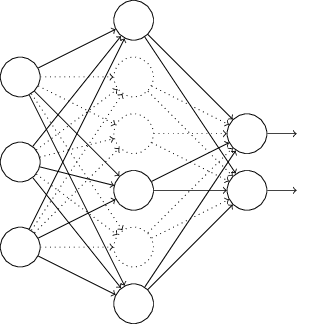
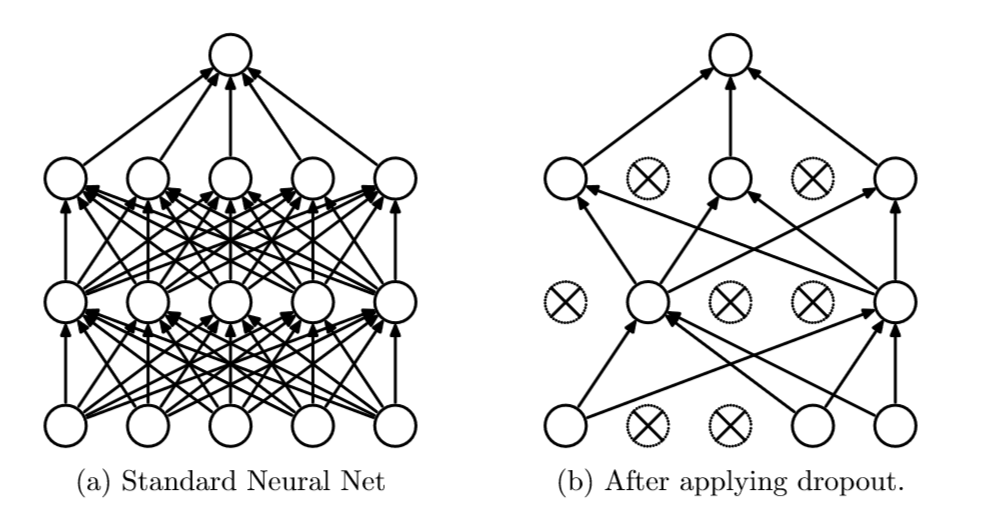
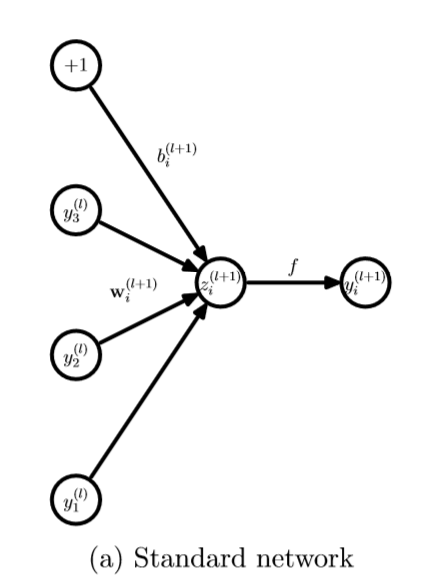
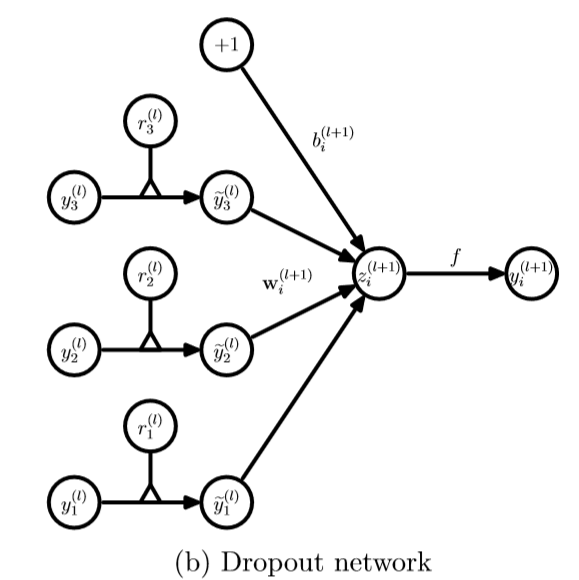
左边是标准神经网络,右边是使用Dropout的神经网络,可见只是连接度少了一些,并不影响模型继续训练。其实,Dropout动机和初衷非常有意思。
文章里也谈到,可以类比人类男性和女性的基因。人类通过成千上万年进化,依然保持着这样的繁衍方式:男人贡献一半基因序列,女人贡献一半基因序列,最后组成后代的完整基因序列。当我们观察男人基因序列中的一个基因片段,它不仅要和男人基因序列很好地组合与配合,在繁衍后代时,也要和女人的那一半基因序列组合和配合,这个较好的一个基因片段一定要在两个情况下都很好的适应才行,这正像神经网络中的一个神经元,它要在各个情况下都很好地适应训练,所以,我们要Dropout一些神经元啊!了解了吧~
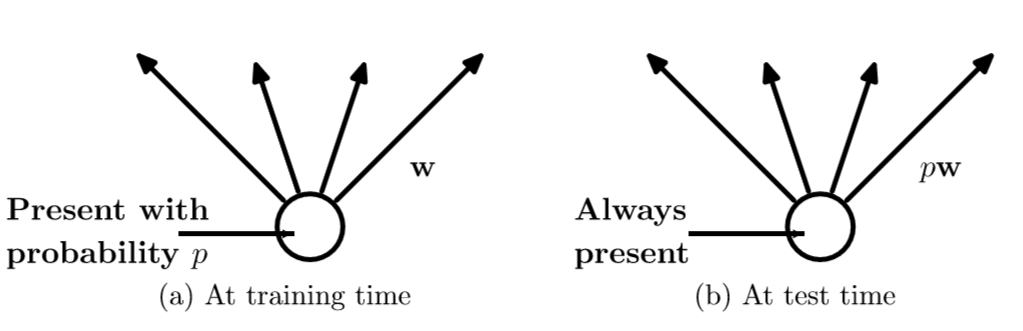
再来关注一个神经元:
需要指出的是,在训练时,权重参数w是共享的。就是说,只要连接权重的神经单元不dropout,那么每次调参时,权重接着调整参数值。换句话说,权重参数个数和不用Dropout的神经网络参数个数是一样的。不同的是,见上图,在训练时,每个神经单元都可能以概率p去除;在测试阶段,每个神经单元都是存在的,权重参数w要乘以p,成为:pw。
接下来看一下,每层Dropout网络和传统网络计算的不同之处:
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
torch.manual_seed(1)
lr = 0.1
N_SAMPLES = 20
N_HIDDEN = 300
# 训练数据
x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
y = x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))
x, y = Variable(x), Variable(y)
# 测试数据
test_x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
test_y = test_x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))
test_x, test_y = Variable(test_x, volatile=True), Variable(test_y, volatile=True)
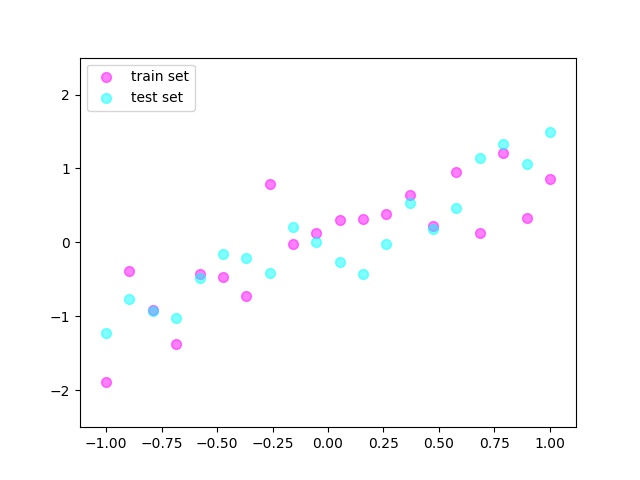
# 展示一下数据分布
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train set')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test set')
plt.legend(loc='upper left')
plt.ylim((-2.5, 2.5))
plt.show()
net_overfitting = torch.nn.Sequential(
torch.nn.Linear(1, N_HIDDEN),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, N_HIDDEN),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, 1),
)
net_dropped = torch.nn.Sequential(
torch.nn.Linear(1, N_HIDDEN),
torch.nn.Dropout(0.5), # drop out 0.5
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, N_HIDDEN),
torch.nn.Dropout(0.5), # drop out 0.5
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, 1),
)
print(net_overfitting) # 会过拟合的网络结构
"""
Sequential (
(0): Linear (1 -> 300)
(1): ReLU ()
(2): Linear (300 -> 300)
(3): ReLU ()
(4): Linear (300 -> 1)
)
"""
print(net_dropped) # 使用了Dropout的网络结构
"""
Sequential (
(0): Linear (1 -> 300)
(1): Dropout (p = 0.5)
(2): ReLU ()
(3): Linear (300 -> 300)
(4): Dropout (p = 0.5)
(5): ReLU ()
(6): Linear (300 -> 1)
)
"""
optimizer_ofit = torch.optim.Adam(net_overfitting.parameters(), lr=lr)
optimizer_drop = torch.optim.Adam(net_dropped.parameters(), lr=lr)
loss_func = torch.nn.MSELoss()
plt.ion() # hold住图
for t in range(500):
pred_ofit = net_overfitting(x)
pred_drop = net_dropped(x)
loss_ofit = loss_func(pred_ofit, y)
loss_drop = loss_func(pred_drop, y)
optimizer_ofit.zero_grad()
optimizer_drop.zero_grad()
loss_ofit.backward()
loss_drop.backward()
optimizer_ofit.step()
optimizer_drop.step()
if t % 10 == 0:
# 切换到测试形态
net_overfitting.eval()
net_dropped.eval()
# 画一下
plt.cla()
test_pred_ofit = net_overfitting(test_x)
test_pred_drop = net_dropped(test_x)
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.3, label='train set')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.3, label='test set')
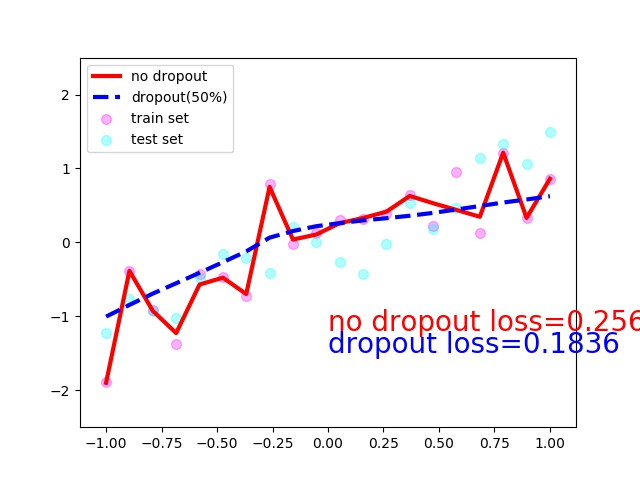
plt.plot(test_x.data.numpy(), test_pred_ofit.data.numpy(), 'r-', lw=3, label='no dropout')
plt.plot(test_x.data.numpy(), test_pred_drop.data.numpy(), 'b--', lw=3, label='dropout(50%)')
plt.text(0, -1.2, 'no dropout loss=%.4f' % loss_func(test_pred_ofit, test_y).data[0], fontdict={'size': 20, 'color': 'red'})
plt.text(0, -1.5, 'dropout loss=%.4f' % loss_func(test_pred_drop, test_y).data[0], fontdict={'size': 20, 'color': 'blue'})
plt.legend(loc='upper left'); plt.ylim((-2.5, 2.5));plt.pause(0.1)
# 切换回训练形态
net_overfitting.train()
net_dropped.train()
plt.ioff()
plt.show()
对PyTorch教程感兴趣的同学,欢迎进入我们的专知PyTorch主题群一起交流、学习、讨论,扫一扫如下群二维码即可进入(先加微信小助手weixinhao: Rancho_Fang,注明PyTorch)。