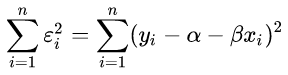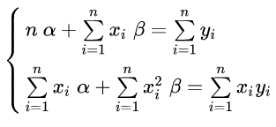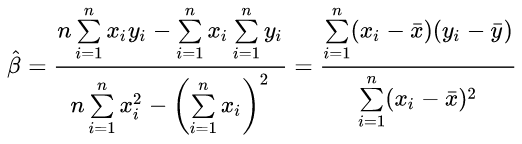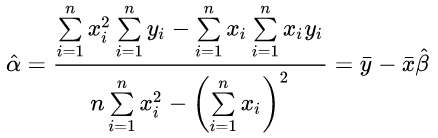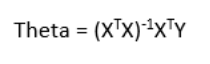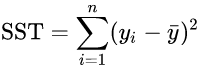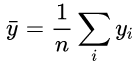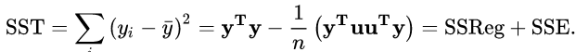线性回归:简单线性回归详解
【导读】本文是一篇专门介绍线性回归的技术文章,讨论了机器学习中线性回归的技术细节。线性回归核心思想是获得最能够拟合数据的直线。文中将线性回归的两种类型:一元线性回归和多元线性回归,本文主要介绍了一元线性回归的技术细节:误差最小化、标准方程系数、使用梯度下降进行优化、残差分析、模型评估等。在文末给出了相关的GitHub地址。
Linear Regression — Detailed View
详细解释线性回归
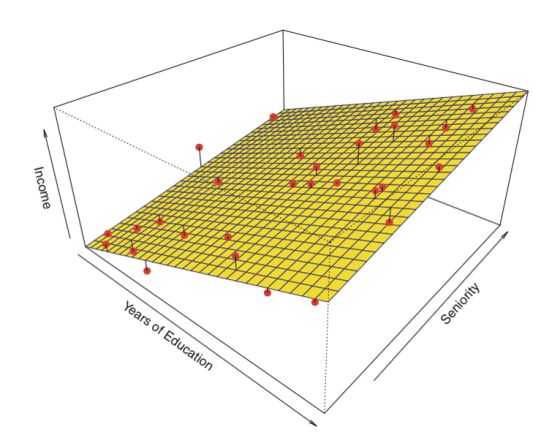
线性回归用于发现目标与一个或多个预测变量之间的线性关系。 有两种类型的线性回归 – 一元线性回归(Simple)和多元线性回归(Multiple)。
一元线性回归
一元线性回归对于寻找两个连续变量之间的关系很有用。一个是预测变量或自变量,另一个是响应或因变量。它寻找统计关系而不是确定性关系。如果一个变量可以被另一个变量精确地表达,那么两个变量之间的关系被认为是确定性的。例如,使用摄氏度的温度,可以准确地预测华氏温度。统计关系在确定两个变量之间的关系时并不准确,例如,身高和体重之间的关系。
线性回归核心思想是获得最能够拟合数据的直线。拟合度最高的直线是总预测误差(所有数据点)尽可能小的直线。误差是用在原始点以及预测点之间的距离来衡量。
完整代码:
https://github.com/SSaishruthi/Linear_Regression_Detailed_Implementation
▌实例
我们有一个数据集,其中包含有关“学习小时数”与“获得的分数”之间关系的信息。已经观察到许多学生,并记录他们的学习时间和成绩。这将是我们的训练数据。目标是设计一个模型,给定学习时间,可以预测成绩。使用训练数据,获得将会给出最小误差的回归线。然后这个线性方程可以用于任何新的数据。也就是说,如果我们将学习时间作为输入,我们的模型应该以最小误差预测它们的分数。
Y(pred)= alpha + beta * x
为了使误差最小化,必须确定alpha和beta。如果平方误差和被用作评估模型的度量,目标是获得最小化这个误差的直线。
如果我们不对这个错误进行平方,那么正面和负面的样本误差就会相互抵消。
为了估计模型的参数alpha和beta,我们已知一组样本(yi, xi)(其中i=1,2,…,n),其计算的目标为最小化残差平方和:
使用微分法求极值:将上式分别对alpha 和 beta 做一阶偏微分,并令其等于0:
此二元一次线性方程组可用克莱姆法则求解,得解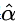
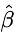
探索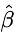
• 如果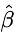
• 如果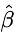
探索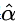
• 如果没有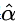
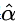
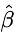
标准方程系数(Co-efficient from Normal equations)
除了上述方程外,模型的系数也可以用标准方程计算。
Theta包含所有预测因子的系数,包括常数项。 标准方程通过对输入矩阵取逆来执行计算。 随着函数数量的增加,计算的复杂性将会增加。 当样本特征维数变大时,求逆会比较耗时。
下面是方程的python实现。
def theta_calc(x_train, y_train):
#Initializing all variables
n_data = x_train.shape[0]
bias = np.ones((n_data,1))
x_train_b = np.append(bias, x_train, axis=1)
#
theta_1 = np.linalg.inv(np.dot(x_train_b.T,x_train_b))
theta_2 = np.dot(theta_1, x_train_b.T)
theta = np.dot(theta_2,y_train)
#
return theta
使用梯度下降进行优化
标准方程的复杂性使其难以使用,可以使用梯度下降进行优化。 对损失函数求偏导数,并给出参数的最优系数值。
梯度下降的Python代码
#gradient descent
def grad_descent(s_slope, s_intercept, l_rate, iter_val, x_train, y_train):
for i in range(iter_val):
int_slope = 0
int_intercept = 0
n_pt = float(len(x_train))
for i in range(len(x_train)):
int_intercept = - (2/n_pt) * (y_train[i] - ((s_slope * x_train[i]) +
s_intercept))
int_slope = - (2/n_pt) * x_train[i] * (y_train[i] - ((s_slope * x_train[i]) +
s_intercept))
final_slope = s_slope - (l_rate * int_slope)
final_intercept = s_intercept - (l_rate * int_intercept)
s_slope = final_slope
s_intercept = final_intercept
return s_slope, s_intercept
残差分析
随机性和不可预测性是回归模型的两个主要组成部分。
预测=确定性+统计(Prediction = Deterministic + Statistic)
确定性部分由模型中的预测变量覆盖。随机部分揭示了预期和观测值不可预测的事实。总会有一些信息被忽略。这些信息可以从残差信息中获得。
我们通过一个例子来解释残差的概念。考虑一下,我们有一个数据集,可以预测给定当天气温,其果汁的销售量。从回归方程预测的值总会与实际值有一些差异。销售额与实际产出值不完全匹配。这种差异称为residue。
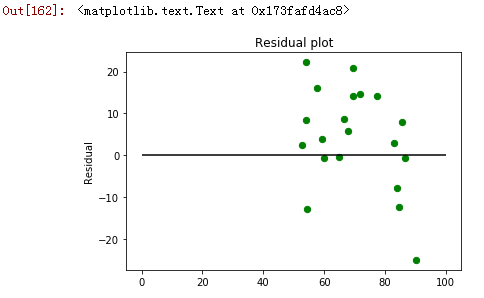
残差示意图有助于使用残差值分析模型。它在预测值和residue之间进行绘制。它们的值是标准化的,该点与0的距离指定了该值的预测有多糟糕。如果该值为正值,则预测值较低。如果该值是负值,那么预测值很高。 0值表示完美的预测。检测残差模式可以改善模型。
残差的特征
• 残差不代表任何模式
• 相邻的残差不应该是相同的,因为它们表明系统漏掉了一些信息。
残差示意图的实现和细节
#Residual plot
plt.scatter(prediction, prediction - y_test, c='g', s = 40)
plt.hlines(y=0, xmin=0, xmax=100)
plt.title('Residual plot')
plt.ylabel('Residual')
模型评估
方差分析
该值的范围从0到1。值“1”表示预测变量完全考虑了Y中的所有变化。值“0”表示预测变量“x”在“y”中没有变化。
总平方和SST (sum of squares for total) 是:
其中
2,回归平方和SSR (sum of squares for regression)
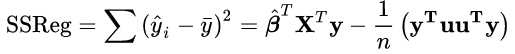
3,残差平方和SSE (sum of squares for error) 是:
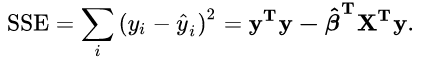
4,总平方和SST又可写做SSReg和SSE的和:
Python 实现
def rsq(prediction, y_test):
#
total_data = len(prediction)
#Average of total prediction
y_avg = np.sum(y_test)/total_data
#total sum of square error
tot_err = np.sum((y_test-y_avg)**2)
#total sum of squared error of residuals
res_err = np.sum((y_test-prediction)**2)
#
r2 = 1 - (res_err / tot_err)
return r2
#defining slope and intercept value as 0
learning_rate = 0.001
start_slope = 0
start_intercept = 0
iteration = 102
#intial run
grad_slope, grad_intercept = grad_descent(start_slope, start_intercept, learning_rate,
iteration, x_train, y_train)
final_e_value, prediction = mse_calc(grad_slope, grad_intercept, x_test, y_test)
#
print('Slope of the model', grad_slope)
print('Intercept of the model', grad_intercept)
print('Error value of the model', final_e_value)
r2_val = rsq(prediction, y_test)
print('R squared value', r2_val)
#Graph
plt.scatter(x_test, y_test)
plt.plot(x_test, prediction, color='blue', linewidth = 3)
plt.xlabel("Input")
plt.ylabel("Output")
plt.show()
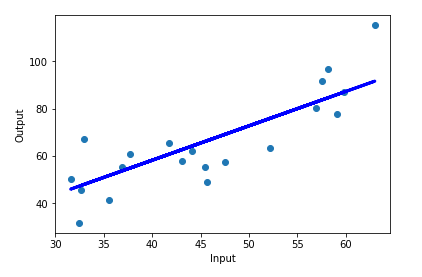
获得回归线:
完整代码:
https://github.com/SSaishruthi/Linear_Regression_Detailed_Implementation
参考链接:https://towardsdatascience.com/linear-regression-detailed-view-ea73175f6e86
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域26个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
同时欢迎各位用户进行专知投稿,详情请点击:
【诚邀】专知诚挚邀请各位专业者加入AI创作者计划!了解使用专知!
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请扫一扫如下二维码关注我们的公众号,获取人工智能的专业知识!
请加专知小助手微信(Rancho_Fang),加入专知主题人工智能群交流!
点击“阅读原文”,使用专知!