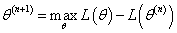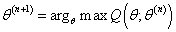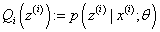2、PLSA与LDA对比

（1）PLSA（Probability Latent Semantic Analysis，概率潜语义分析）

PLSA基本介绍

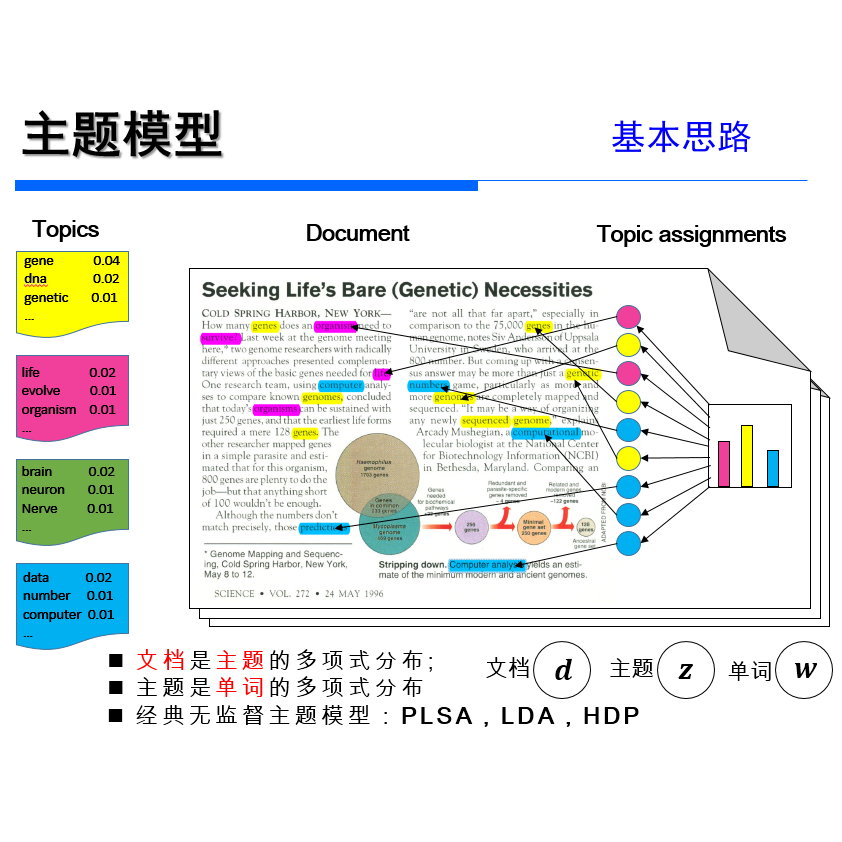
其实LDA主题模型中的“文档——主题——单词”的三层结构并不是LDA中首创的，在概率潜在语义分析中（Probabilistic latent semantic analysis, PLSA）已经提出了这种三层结构，LDA的工作就是在这种结构的基础上增加了贝叶斯框架，使概率主题模型PLSA变成了贝叶斯主题模型LDA。
我们了解到通过SVD可以进行LSA，把给定文档投影到语义空间，但语义的权重不好解释。PLSA是从概率分布的角度建模的一种方法，它假设在词和文档之间有一层主题隐语义，而文档主题符合多项分布，一个主题中的词项也符合多项分布，由这两层分布的模型，生成各种文档。
想象某个人要写N篇文档，他需要确定每篇文档里每个位置上的词。假定他一共有K个可选的主题，有V个可选的词项，所以，他制作了K个V面的 “主题-词项” 骰子，每个骰子对应一个主题，骰子每一面对应要选择的词项。然后，每写一篇文档会再制作一颗K面的“文档-主题”骰子；每写一个词，先扔该骰子选择主题；得到主题的结果后，使用和主题结果对应的那颗“主题-词项”骰子，扔该骰子选择要写的词。他不停的重复如上两个扔骰子步骤，最终完成了这篇文档。重复该方法N次，则写完所有的文档。在这个过程中，我们并未关注词和词之间的出现顺序，所以PLSA也是一种词袋方法；并且我们使用两层概率分布对整个样本空间建模，所以PLSA也是一种混合模型。
具体来说，该模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别 ${z_k} \in \left\{ {{z_1},...,{z_K}} \right\}$ 。有如下三个相关的概率： $P\left( {{d_i}} \right)$ 表示词在文档 ${d_i}$ 中出现的概率， $P\left( {{w_j}|{z_k}} \right)$ 表示某个词 ${w_j}$ 在给定主题 ${z_k}$ 下出现的概率， $P\left( {{z_k}|{d_i}} \right)$ 表示某个主题 ${z_k}$ 在给定文档 ${d_i}$ 下出现的概率。利用这三个概率，我们可以按照如下方式得到“词-文档”的生成模型：
PLSA图模型

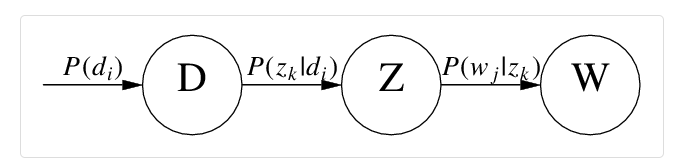
PLSA文档的生成过程：

按照概率 $P\left( {{d_i}} \right)$ 选择一篇文档 ${d_i}$ ；
按照概率 $P\left( {{z_k}|{d_i}} \right)$ 选择一个隐含的主题类别 ${z_k}$ ；
按照概率 $P\left( {{w_j}|{z_k}} \right)$ 生成一个词 ${w_j}$ 。

这样可以得到文档中每个词的生成概率。把这个过程用数学方法表示：

$P\left( {{d_i},{w_j}} \right) = P\left( {{d_i}} \right)P\left( {{w_j}|{d_i}} \right) = P\left( {{d_i}} \right)\sum\limits_{k = 1}^K {P\left( {{w_j}|{z_k}} \right)P\left( {{z_k}|{d_i}} \right)}$

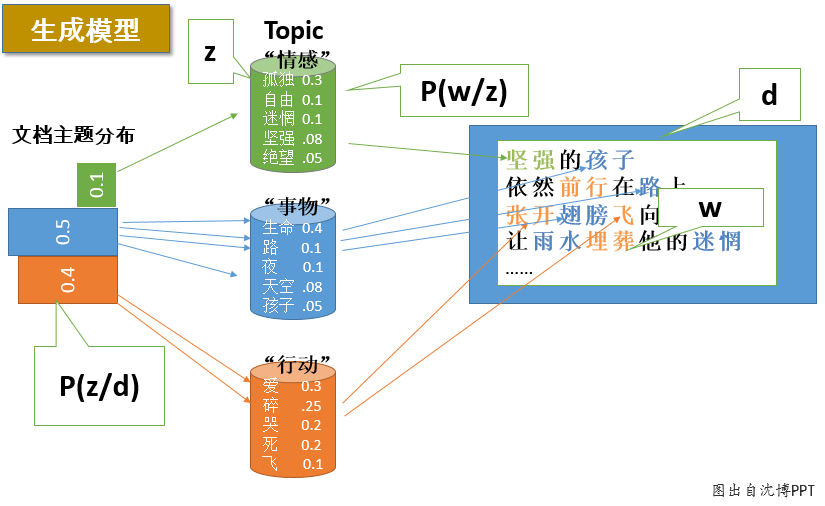
PLSA文档生成过程：例如下图的汪峰写歌词示例：

EM算法介绍

EM算法，全称为Expectation-maximization algorithm，期望最大算法，其基本思想是：首先随机选取一个值去初始化待估计的值 ${\theta ^{\left( 0 \right)}}$ ，然后不断迭代寻找更优的 ${\theta ^{\left( {n + 1} \right)}}$ 使得其likelihood似然函数 $L\left( {{\theta ^{\left( {n + 1} \right)}}} \right)$ 比原来的 $L\left( {{\theta ^{\left( n \right)}}} \right)$ 要大。换言之，假定现在得到了 ${\theta ^{\left( n \right)}}$ ，想求 ${\theta ^{\left( n+1 \right)}}$ ，使得

EM的关键便是要找到 $L\left( \theta \right)$ 的一个下界 $Q\left( {\theta ;{\theta ^{\left( n \right)}}} \right)$ （注： $L\left( \theta \right) = \log p\left( {X|\theta } \right)$ ，其中，X表示已经观察到的随机变量），然后不断最大化这个下界，通过不断求解下界 $Q\left( {\theta ;{\theta ^{\left( n \right)}}} \right)$ 的极大化，从而逼近要求解的似然函数 $L\left( \theta \right)$ 。(注意：LDA的变分推断方法中就使用了EM方法的迭代策略)

所以EM算法的一般步骤为：

随机选取或者根据先验知识初始化 ${\theta ^{\left( 0 \right)}}$ ；
不断迭代下述两步:
(a). 给出当前的参数估计 ${\theta ^{\left( 0 \right)}}$ ，计算似然函数 $L\left( \theta \right)$ 的下界 $Q\left( {\theta ;{\theta ^{\left( n \right)}}} \right)$
(b). 重新估计参数 $\theta$ ，即求 ${\theta ^{\left( {n + 1} \right)}}$ ，使得
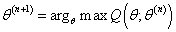
上述第二步后，如果收敛（即收敛）则退出算法，否则继续回到第二步。

下面进行详细介绍：
假定有训练集 $\left\{ {{x^{\left( 1 \right)}}, \ldots ,{x^{\left( m \right)}}} \right\}$ ，包含m个独立样本，希望从中找到该组数据的模型p(x,z)的参数。然后通过极大似然估计建立目标函数–对数似然函数：

$\ell \left( \theta \right) = \sum\limits_{i = 1}^m {\log p\left( {x;\theta } \right)} = \sum\limits_{i = 1}^m {\log \sum\limits_z {p\left( {x,z;\theta } \right)} }$

这里，z是隐随机变量，直接找到参数的估计是很困难的。我们的策略是建立 $\ell \left( \theta \right)$ 的下界，并且求该下界的最大值；重复这个过程，直到收敛到局部最大值。
令 $Q_i$ 是z的某一个分布，Q_i≥0，且结合Jensen不等式，有：

$\begin{array}{c} \sum\limits_i {\log p\left( {{x^{\left( i \right)}};\theta } \right)} = \sum\limits_i {\log \sum\limits_{{z^{\left( i \right)}}} {p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)} } \\ = \sum\limits_i {\log \sum\limits_{{z^{\left( i \right)}}} {{Q_i}\left( {{z^{\left( i \right)}}} \right)\frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}}} } \\ \ge \sum\limits_i {\sum\limits_{{z^{\left( i \right)}}} {{Q_i}\left( {{z^{\left( i \right)}}} \right)\frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}}} } \end{array}$

为了寻找尽量紧的下界，我们可以让使上述等号成立，而若要让等号成立的条件则是：

$\frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}} = c$

换言之，有以下式子成立： ${Q_i}\left( {{z^{\left( i \right)}}} \right) \propto p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)$ ，
且由于有： $\sum\nolimits_z {{Q_i}\left( {{z^{\left( i \right)}}} \right)} = 1$
所以可得：

${Q_i}\left( {{z^{\left( i \right)}}} \right) = \frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{\sum\nolimits_z {p\left( {{x^{\left( i \right)}},z;\theta } \right)} }} = \frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{p\left( {{x^{\left( i \right)}};\theta } \right)}} = p\left( {{z^{\left( i \right)}}|{x^{\left( i \right)}};\theta } \right)$

最终得到EM算法的整体框架如下：

Repeat until convergence {

(E-step) For each i, set
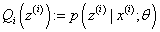
(M-step) Set

}

EM算法估计PLSA的两个未知参数

首先尝试从矩阵的角度来描述待估计的两个未知变量 $P\left( {{w_i}|{z_k}} \right)$ 和 $P\left( {{z_k}|{d_i}} \right)$ 。

假定用 ${\varphi _k}$ 表示词表 $v$ 在主题 $z_k$ 上的一个多项分布，则 ${\varphi _k}$ 可以表示成一个向量，每个元素 ${\varphi _{k,j}}$ 表示词项 ${w_j}$ 出现在主题 ${z_k}$ 中的概率，即:

$P\left( {{w_j}|{z_k}} \right) = {\varphi _{k,j}},\sum\limits_{{w_j} \in \nu } {{\varphi _{k,j}} = 1}$

用 ${\theta _j}$ 表示所有主题 $Z$ 在文档 $d_i$ 上的一个多项分布，则 ${\theta _j}$ 可以表示成一个向量，每个元素 ${\theta _{i,k}}$ 表示主题出现在文档中的概率，即

$P\left( {{z_k}|{d_i}} \right) = {\theta _{i,k}},\sum\limits_{{z_k} \in Z} {{\theta _{i,k}} = 1}$

这样，把 $P\left( {{w_i}|{z_k}} \right)$ 和 $P\left( {{z_k}|{d_i}} \right)$ 转换成了两个矩阵。换言之，最终我们要求解的参数是这两个矩阵：

$\Phi = \left[ {{\varphi _1},...,{\varphi _K}} \right],{z_k} \in Z$

$\Theta = \left[ {{\theta _1},...,{\theta _M}} \right],{d_i} \in D$

由于词和词之间是相互独立的，所以整篇文档N个词的分布为：

$P\left( {W|{d_i}} \right) = \prod\limits_{j = 1}^N {P{{\left( {{d_i},{w_j}} \right)}^{n\left( {{d_i},{w_j}} \right)}}}$

再由于文档和文档之间也是相互独立的，所以整个语料库中词的分布为（整个语料库M篇文档，每篇文档N个词）：

$P\left( {W|D} \right) = \prod\limits_{i = 1}^D {\prod\limits_{j = 1}^N {P{{\left( {{d_i},{w_j}} \right)}^{n\left( {{d_i},{w_j}} \right)}}} }$

其中， $n\left( {{d_i},{w_j}} \right)$ 表示词项 $n\left( {{d_i},{w_j}} \right)$ 在文档 ${d_i}$ 中的词频， $n\left( {{d_i}} \right)$ 表示文档 ${d_i}$ 中词的总数，显然有 $n\left( {{d_i}} \right) = \sum\nolimits_{{w_j} \in \nu } {n\left( {{d_i},{w_j}} \right)}$ 。从而得到整个语料库的主题-词分布的对数似然函数：

$\begin{array}{l} \ell \left( {\Phi ,\Theta } \right) = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {n\left( {{d_i},{w_j}} \right)\log P\left( {{d_i},{w_j}} \right)} } \\ = \sum\limits_{i = 1}^M {n\left( {{d_i}} \right)\left( {\log P\left( {{d_i}} \right) + \sum\limits_{j = 1}^N {\frac{{n\left( {{d_i},{w_j}} \right)}}{{n\left( {{d_i}} \right)}}} } \right)\log \sum\limits_{k = 1}^K {P\left( {{w_j}|{z_k}} \right)} P\left( {{z_k}|{d_i}} \right)} \\ = \sum\limits_{i = 1}^M {n\left( {{d_i}} \right)\left( {\log P\left( {{d_i}} \right) + \sum\limits_{j = 1}^N {\frac{{n\left( {{d_i},{w_j}} \right)}}{{n\left( {{d_i}} \right)}}} } \right)\log \sum\limits_{k = 1}^K {{\varphi _{k,j}}{\theta _{i,k}}} } \end{array}$

现在，我们需要最大化上述这个对数似然函数来求解参数 ${\varphi _{k,j}}$ 和 ${\theta _{i,k}}$ 。对于这种含有隐变量的最大似然估计，可以使用EM算法。EM算法，分为两个步骤：先E-step，后M-step。

E-step：假定参数已知，计算此时隐变量的后验概率。
利用贝叶斯法则，可以得到：

$\begin{array}{l} P\left( {{z_k}|{d_i},{w_j}} \right) = \frac{{P\left( {{z_k},{d_i},{w_j}} \right)}}{{\sum\nolimits_{k = 1}^K {P\left( {{z_k},{d_i},{w_j}} \right)} }}\\ = \frac{{P\left( {{w_j}|{d_i},{z_k}} \right)P\left( {{z_k}|{d_i}} \right)P\left( {{d_i}} \right)}}{{\sum\nolimits_{k = 1}^K {\left( {P\left( {{w_j}|{d_i},{z_k}} \right)P\left( {{z_k}|{d_i}} \right)P\left( {{d_i}} \right)} \right)} }}\\ = \frac{{P\left( {{w_j}|{z_k}} \right)P\left( {{z_k}|{d_i}} \right)}}{{\sum\nolimits_{k = 1}^K {\left( {P\left( {{w_j}|{z_k}} \right)P\left( {{z_k}|{d_i}} \right)} \right)} }}\\ = \frac{{{\varphi _{k,j}}{\theta _{i,k}}}}{{\sum\nolimits_{k = 1}^K {{\varphi _{k,j}}{\theta _{i,k}}} }} \end{array}$

M-step：带入隐变量的后验概率，最大化样本分布的对数似然函数，求解相应的参数。

观察之前得到的对数似然函数 $\ell \left( {\Phi ,\Theta } \right)$ 的结果，由于文档长度 $P\left( {{d_i}} \right) \propto n\left( {{d_i}} \right)$ 可以单独计算，所以去掉它不影响最大化似然函数。此外，根据E-step的计算结果，把 ${\phi _{k,j}}{\theta _{i,k}} = P\left( {{z_k}|{d_i},{w_j}} \right)\sum\nolimits_{k = 1}^K {{\phi _{l,j}}{\theta _{i,k}}}$ 代入 $\ell \left( {\Phi ,\Theta } \right)$ ，于是我们只要最大化下面这个函数即可：

$\ell = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {n\left( {{d_i},{w_j}} \right)} } \sum\limits_{k = 1}^K {P\left( {{z_k}|{d_i},{w_j}} \right)\log \left[ {{\varphi _{k,j}}{\theta _{i,k}}} \right]}$

这是一个多元函数求极值问题，并且已知有如下约束条件：

$\sum\limits_{j = 1}^N {{\varphi _{k,j}}} = 1$

$\sum\limits_{k = 1}^K {{\theta _{i,k}}} = 1$

一般处理这种带有约束条件的极值问题，常用的方法便是拉格朗日乘数法，即通过引入拉格朗日乘子将约束条件和多元（目标）函数融合到一起，转化为无约束条件的极值问题。

这里我们引入两个拉格朗日乘子 $\tau$
和 $\rho$ ，从而写出拉格朗日函数：

${H} = {{L}^c} + \sum\limits_{k = 1}^K {{\tau _k}\left( {1 - \sum\limits_{j = 1}^N {{\phi _{k,j}}} } \right) + \sum\limits_{i = 1}^M {{\rho _i}\left( {1 - \sum\limits_{k = 1}^K {{\theta _{i,k}}} } \right)}}$

因为我们要求解的参数是 ${\theta _{i,k}}$ 和 ${\varphi _{k,j}}$ ，所以分别对 ${\theta _{i,k}}$ 和 ${\varphi _{k,j}}$ 求偏导，然后令偏导结果等于0，得到：

$\sum\limits_{i = 1}^M {n\left( {{d_i},{w_j}} \right)P\left( {{z_k}|{d_i},{w_j}} \right)} - {\rho _i}{\theta _{i,k}} = 0, 1 \le i \le M,1 \le k \le K$

$\sum\limits_{j = 1}^N {n\left( {{d_i},{w_j}} \right)P\left( {{z_k}|{d_i},{w_j}} \right)} - {\tau _k}{\varphi _{k,j}} = 0, 1 \le j \le N,1 \le k \le K$

消去拉格朗日乘子，最终可估计出参数 ${\theta _{i,k}}$ 和 ${\varphi _{k,j}}$ ：

${\theta _{i,k}} = \frac{{\sum\nolimits_{i = 1}^M {n\left( {{d_i},{w_j}} \right)P\left( {{z_k}|{d_i},{w_j}} \right)} }}{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {n\left( {{d_i},{w_j}} \right)P\left( {{z_k}|{d_i},{w_j}} \right)} } }}$

${\varphi _{k,j}} = \frac{{\sum\nolimits_{j = 1}^N {n\left( {{d_i},{w_j}} \right)P\left( {{z_k}|{d_i},{w_j}} \right)} }}{{n\left( {{d_i}} \right)}}$

（2）LDA（Latent Dirichlet Allocation，隐含狄利克雷分布）

贝叶斯思想

如果你对LDA有了一定的理解，那么你应该知道，LDA其实是在PLSA的基础上加了一层贝叶斯框架。在上面参数估计方法中，我们已经详细介绍了最大似然估计，最大后验估计和贝叶斯估计的三种形式，本节中，我们将再次强调一下LDA的贝叶斯思想。根据wiki百科介绍：

贝叶斯定理是关于随机事件A和B的条件概率的一则定理。

$P\left( {A|B} \right) = \frac{{P\left( {B|A} \right)P\left( A \right)}}{{P\left( B \right)}}$

其中P(A|B)是在B发生的情况下A发生的可能性。

在贝叶斯定理中，每个名词都有约定俗成的名称：

P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
P(A)是A的先验概率（或边缘概率）。之所以称为"先验"是因为它不考虑任何B方面的因素。
P(B)是B的先验概率或边缘概率

按这些术语，贝叶斯定理可表述为：

后验概率 = (相似度*先验概率)/标准化常量

也就是说，后验概率与先验概率和相似度的乘积成正比。

LDA是基于贝叶斯模型的，涉及到贝叶斯模型离不开“先验分布”，“数据（似然）”和"后验分布"三块。在在贝叶斯学派认为：

先验分布 + 数据（似然）= 后验分布

这点其实很好理解，因为这符合我们人的思维方式，举个例子。比如你对好人和坏人的认知，先验分布为：100个好人和100个的坏人，即你认为好人坏人各占一半，现在你被2个好人（数据）帮助了和1个坏人骗了，于是你得到了新的后验分布为：102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布，当你被1个好人（数据）帮助了和3个坏人（数据）骗了后，你又更新了你的后验分布为：103个好人和104个的坏人。依次继续更新下去。

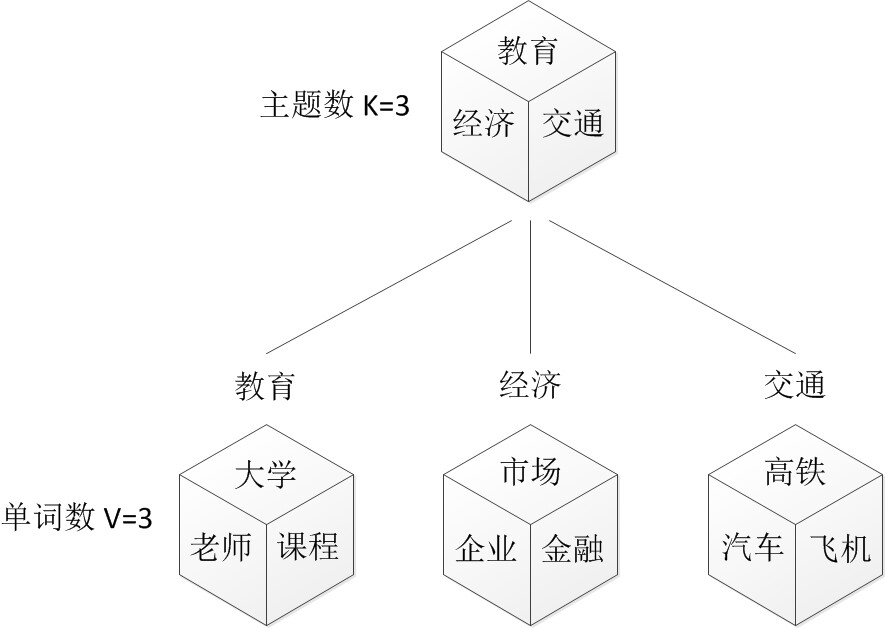
LDA介绍

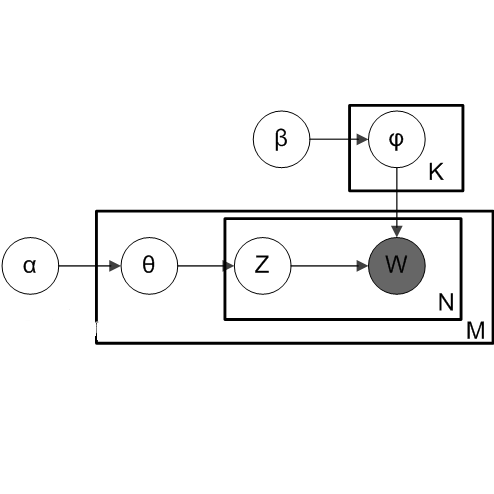
如上图所示，在LDA中，“文档-主题”向量 ${\vec \theta _m}$ 由超参数为 $\vec \alpha$
的Dirichlet分布生成，“主题-词项”向量 ${\vec \varphi _k}$ 由超参数为 $\vec \beta$ 的Dirichlet分布生成，根据概率图，整个样本集合的生成过程如下：

对所有的主题 $k \in \left[ {1,K} \right]$ (生成 $\Phi$ ， $K \times N$ 矩阵)：
- 生成“主题-词项”分布 ${\vec \varphi _k} \sim Dir\left( {\vec \beta } \right)$ ( N维矩阵，对应词表V 中的每个词项的概率)
对所有的文档 $m \in \left[ {1,M} \right]$ ：
- 生成当前文档 m 相应的“文档-主题”分布 ${\vec \theta _m} \sim Dir\left( {\vec \alpha } \right)$ ( K 维向量，即第 m 篇文档对应的每个主题的概率)
- 生成当前文档 m 的长度 ${N_m} \sim Poiss\left( \xi \right)$
- 对当前文档 m 中的所有词 $n \in \left[ {1,{N_m}} \right]$
  - 生成当前位置的词的所属主题 ${z_{m,n}} \sim Mult\left( {{{\vec \theta }_m}} \right)$
  - 根据之前生成的主题分布 $\Phi$ ，生成当前位置的词的相应词项 ${w_{m,n}} \sim Mult\left( {{{\vec \varphi }_{{z_{m,n}}}}} \right)$

根据所有已知信息和带超参数的隐变量，我们可以写出联合分布：

$p\left( {{{\vec w}_m},{{\vec z}_m},{{\vec \theta }_m},\Phi |\vec \alpha ,\vec \beta } \right) = \prod\limits_{n = 1}^{{N_m}} {p\left( {{w_{m,n}}|{{\vec \varphi }_{{z_{m,n}}}}} \right)p\left( {{z_{m,n}}|{{\vec \theta }_m}} \right) \cdot p\left( {{{\vec \theta }_m}|\vec \alpha } \right) \cdot p\left( {\Phi |\vec \beta } \right)}$

通过对 $\Theta = \left\{ {{{\vec \theta }_m}} \right\}_{m = 1}^M$ 和 $\Phi = \left\{ {{{\vec \varphi }_k}} \right\}_{k = 1}^K$ 积分以及 ${z_{m,n}}$ 求和，可以求得 ${w_{m,n}}$ 的分布：

$\begin{array}{l} p\left( {{{\vec w}_m}|\vec \alpha ,\vec \beta } \right)\\ = \int {\int {p\left( {{{\vec \theta }_m}|\vec \alpha } \right) \cdot p\left( {\Phi |\vec \beta } \right)} } \prod\limits_{n = 1}^{{N_m}} {\sum\limits_{{z_{m,n}}} {p\left( {{w_{m,n}}|{{\vec \varphi }_{{z_{m,n}}}}} \right)p\left( {{z_{m,n}}|{{\vec \theta }_m}} \right)d\Phi d{{\vec \theta }_m}} } \\ = \int {\int {p\left( {{{\vec \theta }_m}|\vec \alpha } \right) \cdot p\left( {\Phi |\vec \beta } \right)} } \cdot \prod\limits_{n = 1}^{{N_m}} {p\left( {{w_{m,n}}|{{\vec \theta }_m},\Phi } \right)d\Phi d{{\vec \theta }_m}} \end{array}$

整个样本的分布：

$p\left( {W|\vec \alpha ,\vec \beta } \right) = \prod\limits_{m = 1}^M {p\left( {{{\vec w}_m}|\vec \alpha ,\vec \beta } \right)}$

符号解释：

M: 文档数(固定值)
K: 主题(topic)数(固定值)
V: 词项数(固定值)
$\vec \alpha$ :“文档-主题”分布的超参数( K 维向量，如果对称(symmetric)参数，则是一个标量)
$\vec \beta$ :“主题-词项”分布的超参数( V 维向量，如果对称参数，则是一个标量)
${\vec \theta _m}$ :对于文档 m 的主题分布参数标记 $p\left( {z|d = m} \right)$ ，每篇文档均不同， $\Theta = \left\{ {{{\vec \theta }_m}} \right\}_{m = 1}^M$ 是一个 $M \times K$ 矩阵
${\vec \varphi _k}$ :对于主题 k 的词项分布参数标记 $p\left( {t|z = k} \right)$ ，每个主题均不同， $\Phi = \left\{ {{{\vec \varphi }_k}} \right\}_{k = 1}^K$ 是一个 $K \times V$ 矩阵
文档 m 的长度，这里由Poisson分布决定
${z_{m,n}}$ :文档 m 中第 n 个词所属的主题
${w_{m,n}}$ :文档 m 中第 n 个词的词项

（3）PLSA与LDA生成过程对比

文档生成过程

本节内容主要引用July的博客“通俗理解LDA主题模型”。

PLSA：

假设你要写M篇文档，由于一篇文档由各个不同的词组成，所以你需要确定每篇文档里每个位置上的词。再假定你一共有K个可选的主题，有V个可选的词，咱们来玩一个扔骰子的游戏。如下图所示：

假设你每写一篇文档会制作一颗K面的“文档-主题”骰子（扔此骰子能得到K个主题中的任意一个），和K个V面的“主题-词项”
骰子（每个骰子对应一个主题，K个骰子对应之前的K个主题，且骰子的每一面对应要选择的词项，V个面对应着V个可选的词）。
每写一个词，先扔该“文档-主题”骰子选择主题，得到主题的结果后，使用和主题结果对应的那颗“主题-词项”骰子，扔该骰子选择要写的词。
最后，你不停的重复扔“文档-主题”骰子和”主题-词项“骰子，重复N次（产生N个词），完成一篇文档，重复这产生一篇文档的方法M次，则完成M篇文档。

上述过程抽象出来即是PLSA的文档生成模型。在这个过程中，我们并未关注词和词之间的出现顺序，所以PLSA是一种词袋方法。具体说来，该模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别 ${z_k} \in \left\{ {{z_1},...,{z_K}} \right\}$ 。

则根据这个例子，“文档——主题——单词”的生成过程可描述为：

按照概率 $p\left( {{d_i}} \right)$ 选择一篇文档 ${d_i}$
选定文档 ${d_i}$ 后，从文档-主题分布中按照概率 $p\left( {{z_k}|{d_i}} \right)$ 选择一个隐含的主题类别 ${z_k}$
选定 ${z_k}$ 后，从主题-词分布中按照概率 $P\left( {{w_j}|{z_k}} \right)$ 选择一个词 ${w_j}$

符号定义如下：

$p\left( {{d_i}} \right)$ 表示海量文档中某篇文档被选中的概率。
$P\left( {{w_j}|{d_i}} \right)$ 表示词 ${w_j}$ 在给定文档 ${d_i}$ 中出现的概率。
- 怎么计算得到呢？针对海量文档，对所有文档进行分词后，得到一个词汇列表，这样每篇文档就是一个词语的集合。对于每个词语，用它在文档中出现的次数除以文档中词语总的数目便是它在文档中出现的概率 $P\left( {{w_j}|{d_i}} \right)$ 。
$p\left( {{z_k}|{d_i}} \right)$ 表示具体某个主题 ${z_j}$ 在给定文档 ${d_i}$ 下出现的概率。
$P\left( {{w_j}|{z_k}} \right)$ 表示具体某个词 ${w_j}$ 在给定主题 ${z_k}$ 下出现的概率，与主题关系越密切的词，其条件概率 $P\left( {{w_j}|{z_k}} \right)$ 越大。

LDA：

在PLSA中，选主题和选词都是两个随机的过程，先从文档-主题分布{教育：0.5，经济：0.3，交通：0.2}中抽取出主题：教育，然后从该主题对应的主题-词分布{大学：0.5，老师：0.3，课程：0.2}中抽取出词：大学。而在LDA中，选主题和选词依然都是两个随机的过程，依然可能是先从文档-主题分布{教育：0.5，经济：0.3，交通：0.2}中抽取出主题：教育，然后再从该主题对应的主题-词分布{大学：0.5，老师：0.3，课程：0.2}中抽取出词：大学。但是：

在PLSA中，文档-主题分布和主题-词分布是唯一确定的，能明确的指出文档-主题分布可能就是{教育：0.5，经济：0.3，交通：0.2}，主题-词分布可能就是{大学：0.5，老师：0.3，课程：0.2}。
但在LDA中，文档-主题分布和主题-词分布不再唯一确定不变，即无法确切给出。例如文档-主题分布可能是{教育：0.5，经济：0.3，交通：0.2}，也可能是{教育：0.6，经济：0.2，交通：0.2}，到底是哪个我们不再确定（即不知道），因为它是随机的可变化的。但再怎么变化，也依然服从一定的分布，即文档-主题分布和主题-词分布由Dirichlet先验随机确定。

如下图11和图12不同的生成过程：

图11：PLSA“文档-主题-单词”生成过程

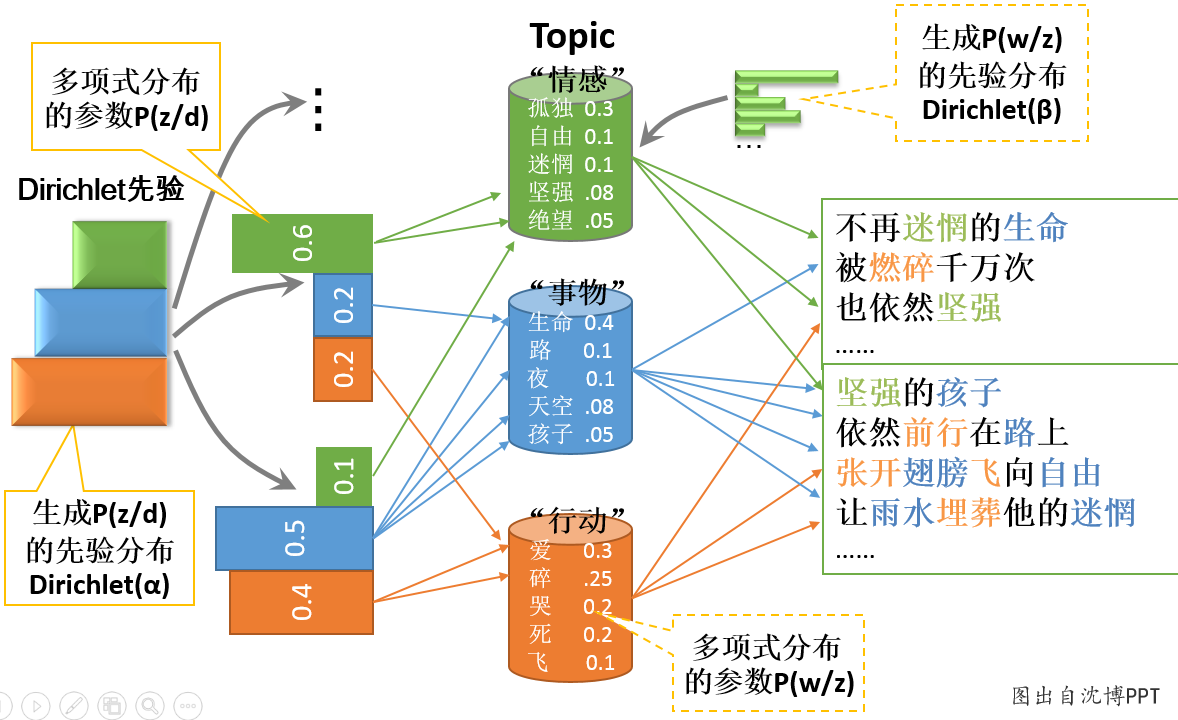
图12：LDA“文档-主题-单词”生成过程

总体来说，LDA是PLSA的贝叶斯版本，所以文档-主题分布和主题-词分布本身由先验知识随机给定。

因此，在PLSA中，文档-主题分布和主题-词分布确定后，以一定的概率（ $p\left( {{z_k}|{d_i}} \right)$ 、 $P\left( {{w_j}|{z_k}} \right)$ ）分别选取具体的主题和词项，生成好文档。而后根据生成好的文档反推其文档-主题分布、主题-词分布时，最终用EM算法（极大似然估计思想）求解出了两个未知但固定的参数的值： ${\phi _{k,j}}$ （由 $P\left( {{w_j}|{z_k}} \right)$ 转换而来）和 ${\theta _{i,k}}$ （ $p\left( {{z_k}|{d_i}} \right)$ 由转换而来）

LDA中，我们不再认为文档-主题分布（各个主题在文档中出现的概率分布）和主题-词分布（各个词语在某个主题下出现的概率分布）是唯一确定的（而是随机变量），而是有很多种可能。但一篇文档总得对应一个文档-主题分布和一个主题-词分布吧，怎么办呢？LDA为它们弄了两个Dirichlet先验参数，这个Dirichlet先验为某篇文档随机抽取出某个文档-主题分布和主题-词分布。

换言之，LDA在PLSA的基础上给这两参数（ $p\left( {{z_k}|{d_i}} \right)$ 、 $P\left( {{w_j}|{z_k}} \right)$ ）加了两个先验分布的参数（贝叶斯化）：一个文档-主题分布的先验分布Dirichlet分布 ${\vec \theta _m} \sim Dir\left( {\vec \alpha } \right)$ ，和一个主题-词分布的先验分布Dirichlet分布 ${\vec \varphi _k} \sim Dir\left( {\vec \beta } \right)$ 。所以，PLSA跟LDA的本质区别就在于它们去估计未知参数所采用的思想不同，前者用的是频率派思想，后者用的是贝叶斯派思想。

频率派思想和贝叶斯派思想的认识，举个例子如下，如我去一朋友家：

按照频率派的思想，我估计他在家的概率是1/2，不在家的概率也是1/2，是个定值。
而按照贝叶斯派的思想，他在家不在家的概率不再认为是个定值1/2，而是随机变量。比如按照我们的经验（比如当天周末），猜测他在家的概率是0.6，但这个0.6不是说就是完全确定的，也有可能是0.7。如此，贝叶斯派没法确切给出参数的确定值（0.3,0.4，0.6,0.7，0.8,0.9都有可能），但至少明白在哪个范围或哪些取值（0.6,0.7，0.8,0.9）更有可能，哪个范围或哪些取值（0.3,0.4）
不太可能。进一步，贝叶斯估计中，参数的多个估计值服从一定的先验分布，而后根据实践获得的数据（例如周末不断跑他家），不断修正之前的参数估计，从先验分布慢慢过渡到后验分布。

参考文献

Blei D M, Ng A Y, Jordan M I. Latent dirichlet allocation[M]. JMLR, 2003. —LDA原始论文
http://blog.csdn.net/v_july_v/article/details/41209515 —July blog通俗理解LDA主题模型
http://vdisk.weibo.com/s/zrFL6OXKgKMAf —Machine Learning读书会第8期上，沈博讲主题模型的PPT
http://www.arbylon.net/publications/text-est.pdf —《Parameter estimation for text analysis》
http://itfish.net/article/61104.html —贝叶斯公式、参数估计
http://blog.jqian.net/post/plsa.html —BLOG | 逍遥郡（主题模型之pLSA）
http://blog.jqian.net/post/lda.html —BLOG | 逍遥郡（主题模型之LDA）
PLSA原始论文—Hofmann T. Probabilistic latent semantic analysis[C]// Fifteenth Conference on Uncertainty in Artificial Intelligence. Morgan
Kaufmann Publishers Inc. 1999:289-296.
rickjin的LDA数学八卦—http://vdisk.weibo.com/s/q0sGh/1360334108?utm_source=weibolife
马晨的LDA算法漫游指南—https://yuedu.baidu.com/ebook/d0b441a8ccbff121dd36839a.html
July blog贝叶斯方法介绍—http://blog.csdn.net/v_july_v/article/details/40984699#t6

展开全文

阅读 8+

评论 0+