春节充电系列：李宏毅2017机器学习课程学习笔记07之反向传播（Back Propagation）- 专知

春节充电系列：李宏毅2017机器学习课程学习笔记07之反向传播（Back Propagation）

课件网址：

http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html

视频网址：

https://www.bilibili.com/video/av15889450/index_1.html

李宏毅机器学习笔记7 反向传播（Back Propagation）

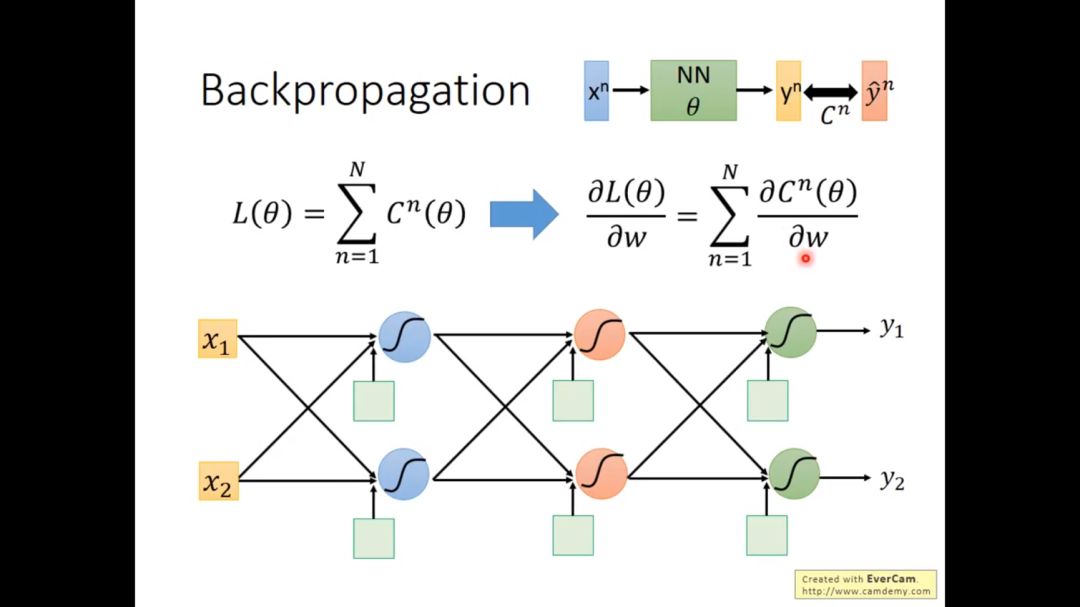
在上一次笔记中我们讨论到在深度学习中，我们寻找好的参数得到我们想要的输出结果，得到参数的方法就是梯度下降方法，为了有效计算梯度，我们采用的是backpropagation方法

1. 链式法则

在数学分析课程中，涉及到复合函数的求导，我们会使用链式法则

由于神经网络是多个神经元级联起来的，涉及微分问题自然会用到链式法则

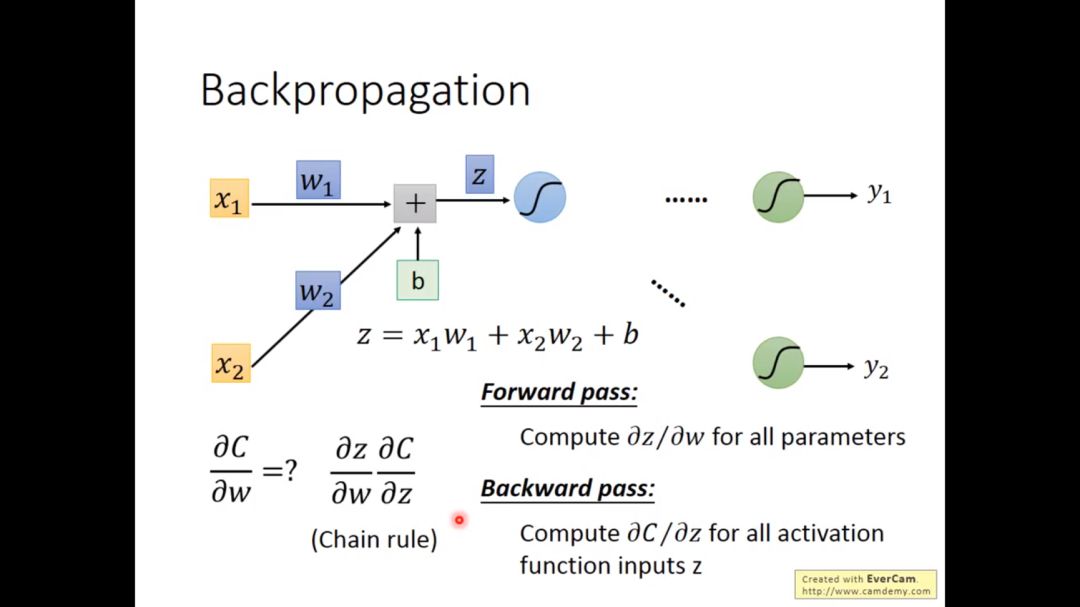
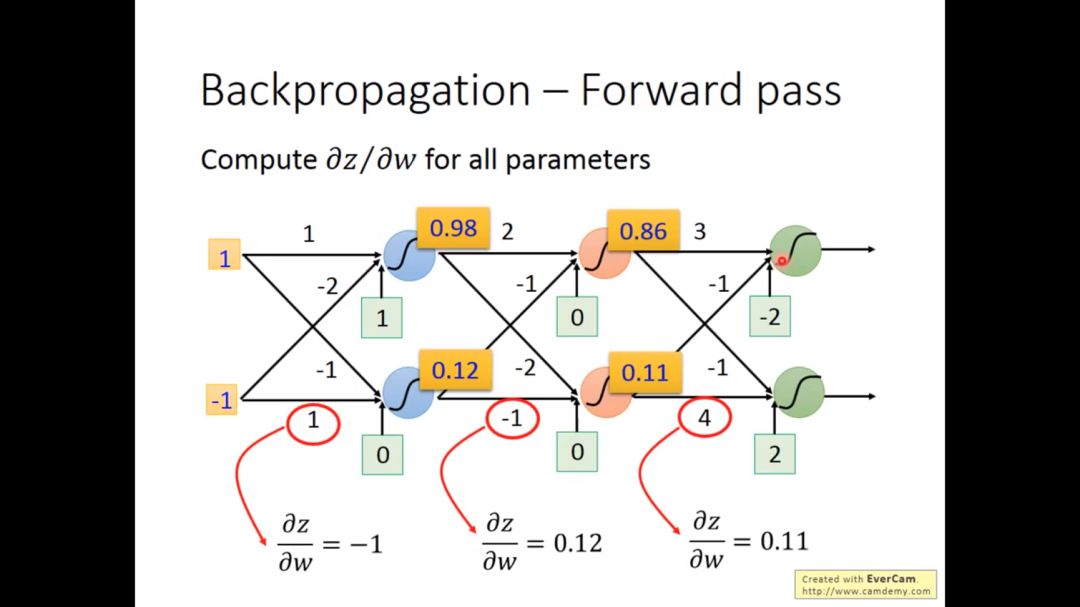
2. forward pass

c对w的微分可以分解为c先对z微分，然后z对w微分

其中c对w的微分很容易求得，这个过程称为forword pass

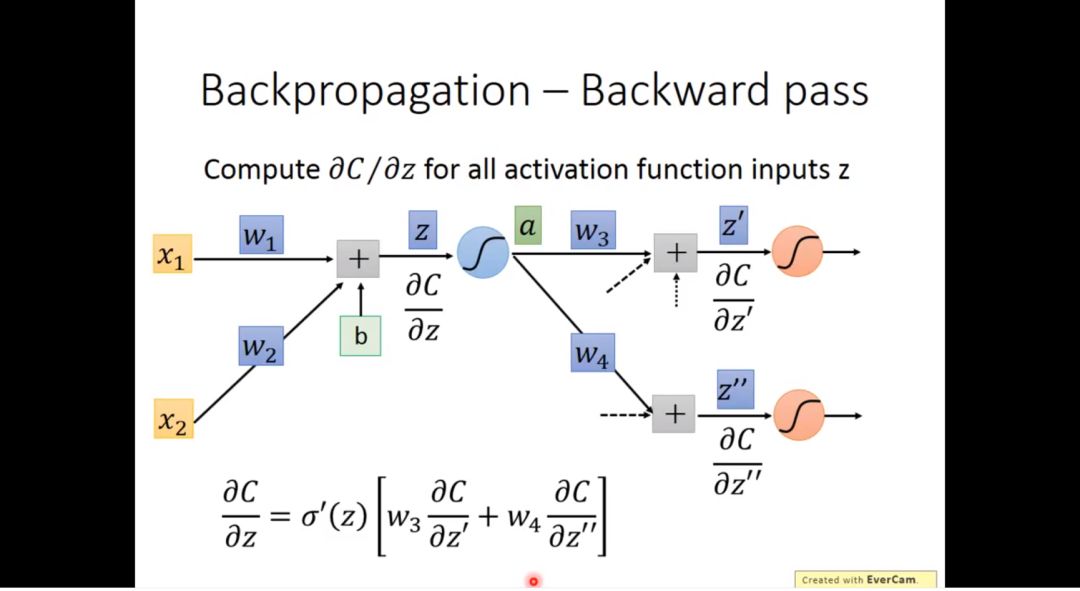
3. backward pass

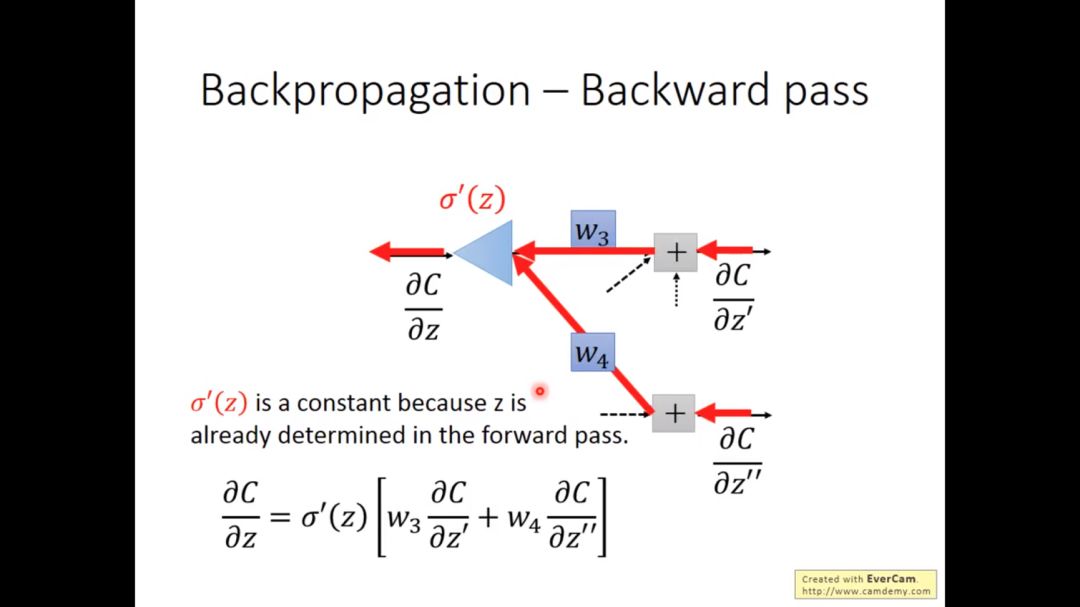
但c对z微分我们现在还不知道，因为该神经元后面的结构我们不知道，假设z通过激活函数后是a，a影响z’,z’’，再利用链式法则我们可以得到

通过上图我们观察到，如果c对z’,z’’的微分知道，c对z的微分等于一个线性函数乘以一个sigmoid函数的导数，这种函数形式和之前介绍的神经元的函数形式很类似，所以我们可以用类似的形式表示

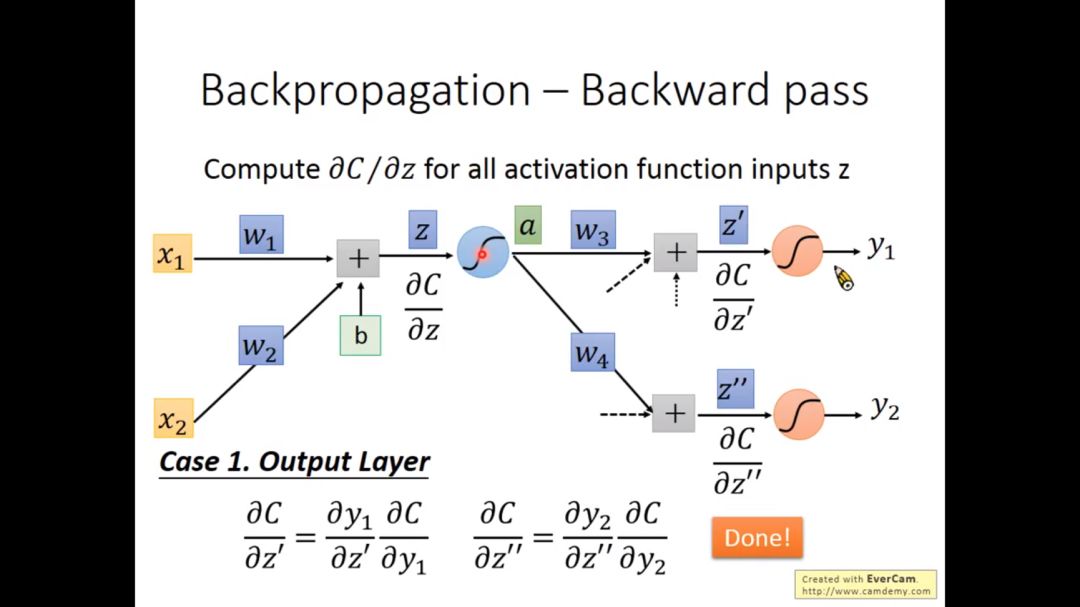
如果z’和z’’是输出层，那么最终结果很容易求得

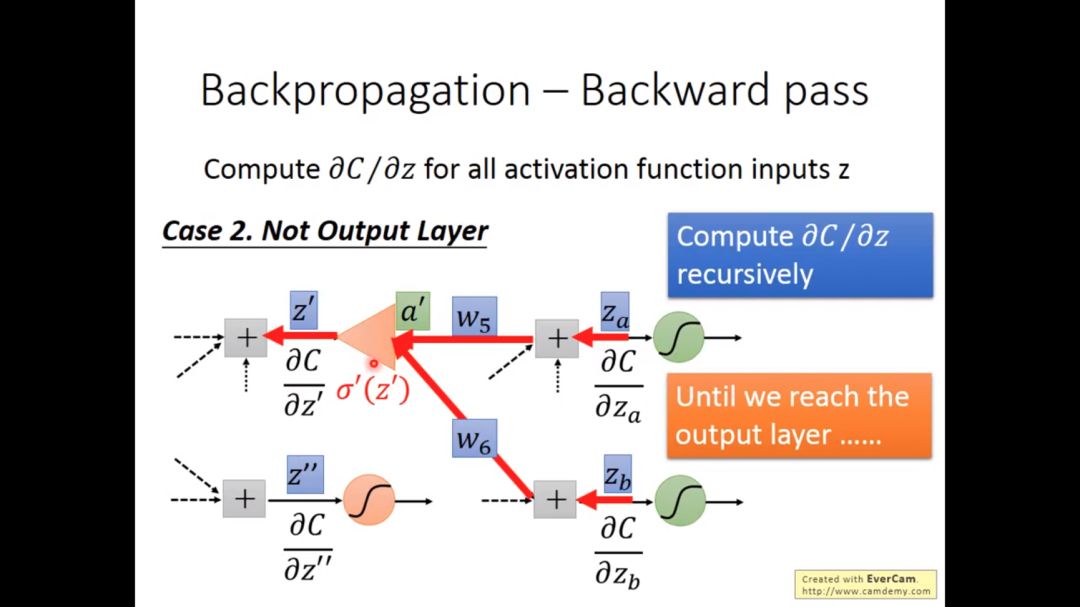
如果z’,z’’不是输出层，我们可以递归继续求解，直到达到输出层

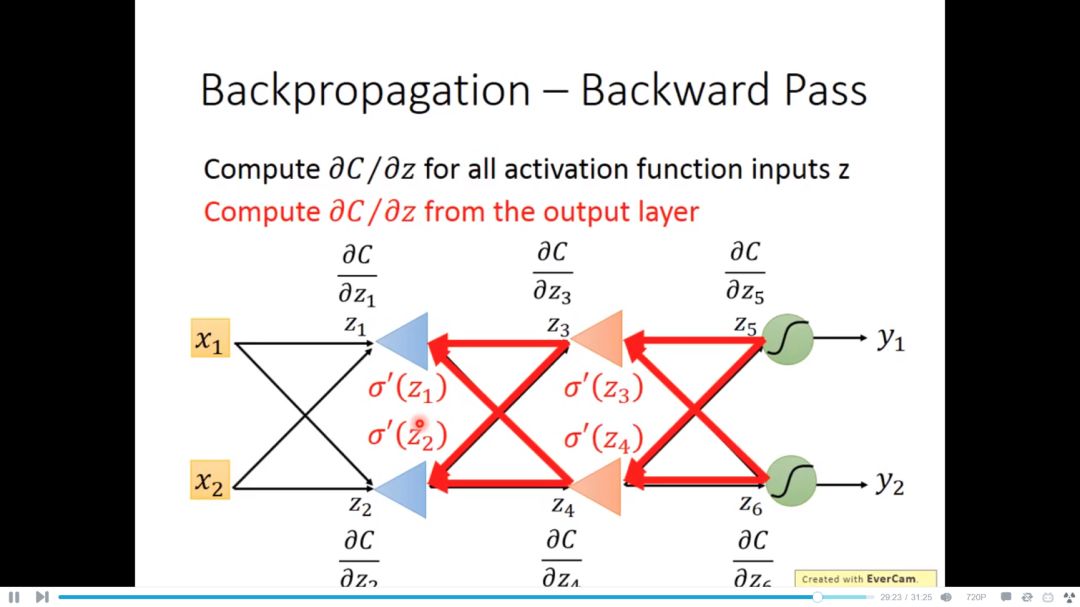
总结上述过程，我们可以先从输出层求得c对z的微分，然后利用backward pass推得的公式从后到前依次推理求解，这也是为什么这个方法叫做backpropagation的原因

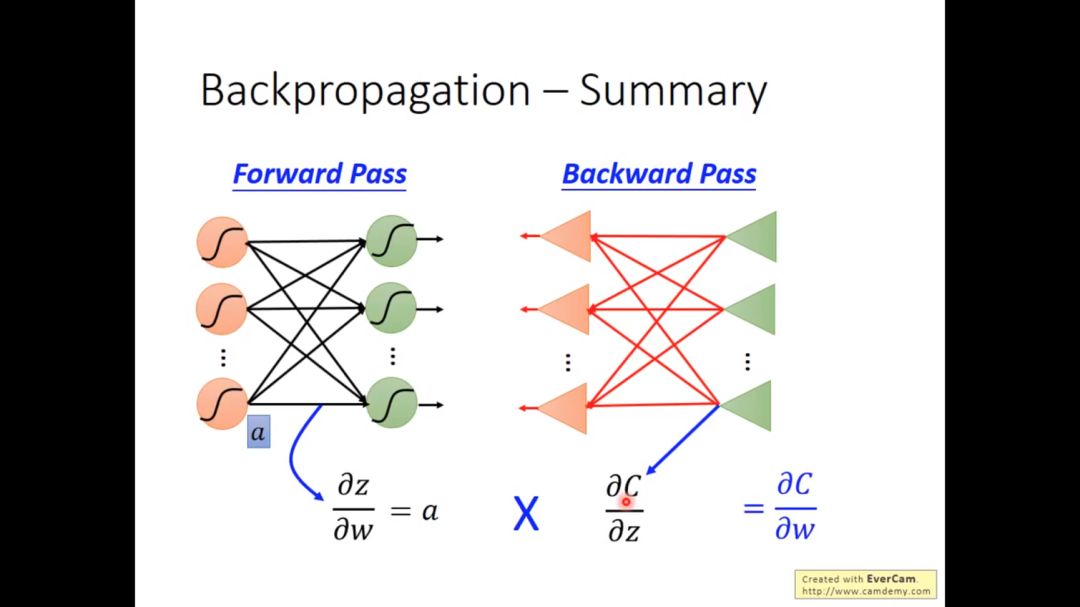
4. summary

最后一步当然是z对w的微分和c对z的微分相乘

请关注专知公众号（扫一扫最下面专知二维码，或者点击上方蓝色专知），

-END-

专 · 知

同时欢迎各位用户进行专知投稿，详情请点击：

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！

点击“阅读原文”，使用专知！

展开全文