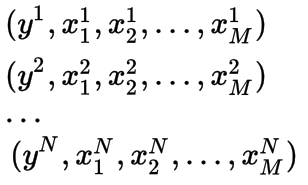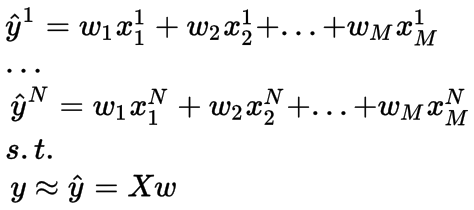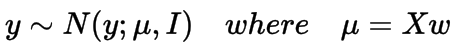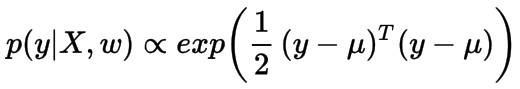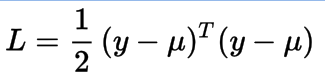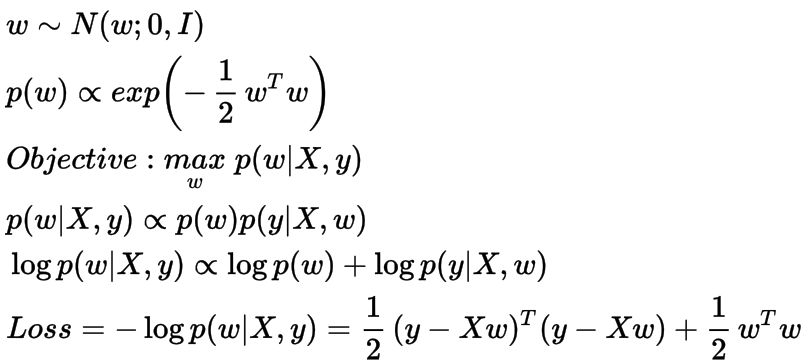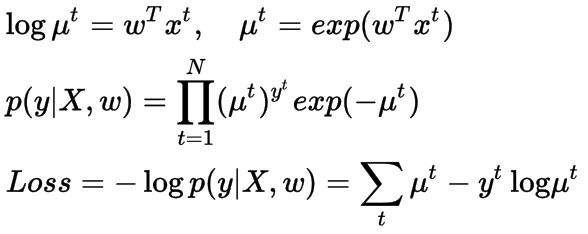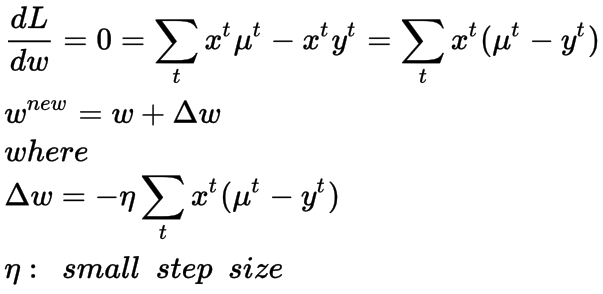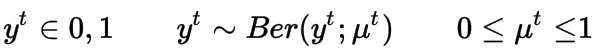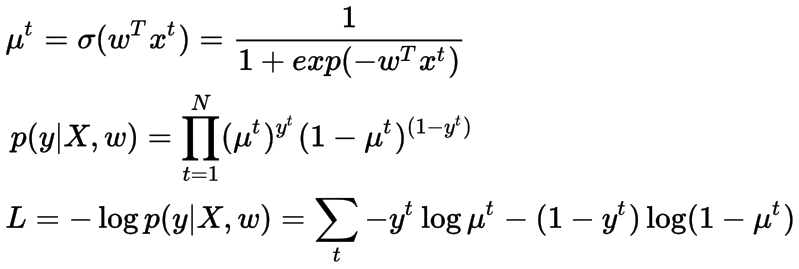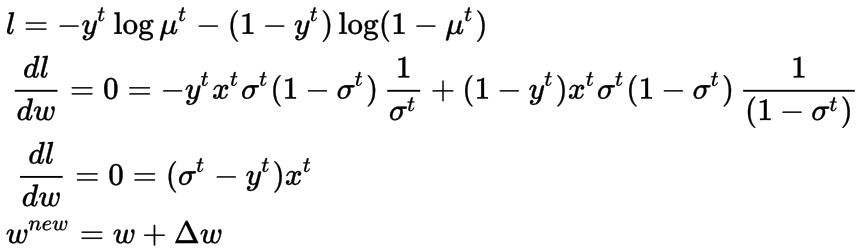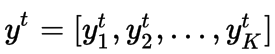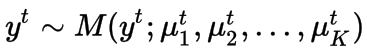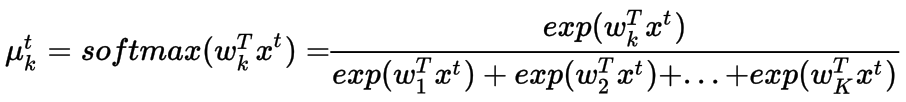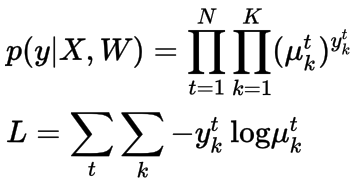深入广义线性模型:分类和回归
【导读】本文来自AI科学家Semih Akbayrak的一篇博文,文章主要讨论了广义的线性模型,包括:监督学习中的分类和回归两类问题。虽然关于该类问题的介绍文章已经很多,但是本文详细介绍了几种回归和分类方法的推导过程,内容涉及:线性回归、最大似然估计、MAP、泊松回归、Logistic回归、交叉熵损失函数、多项Logistic回归等,基本上涵盖了线性模型中的主要方法和问题,非常适合新手入门线性模型。专知内容组编辑整理。
Generalized Linear Models
今天的主题是广义线性模型(GeneralizedLinear Models),一组用于监督学习问题(回归和分类)的通用机器学习模型。
我们从线性回归模型开始吧。我认为,每个人在学习期间都会以某种方式遇到线性回归模型。线性回归模型的目标是在观察到的特征和观察到的实际输出之间找到一个线性映射,以便当我们看到一个新的示例时,我们可以预测输出。在这篇文章中,我们有N个观测样本,其输出是y,每一个观测样本x有M个特征,这些信息用于训练。
我们定义一个M维向量w来表示将输入映射到输出的权重。我们用N*M维矩阵 X来表示所有的输入。 y被定义为N维输出向量。
图显示我们试着使Xw拟合实际输出值y
我们的目标是找到最好的参数w使真实输出向量y和近似值X*w之间的欧式距离最小。为此,我们通常使用最小二乘误差和矩阵运算来最小化它。这里我们用L表示损失(误差)函数。
图表示线性回归问题中如何优化参数w
上面只是把线性回归这个问题使用线性代数的方式进行分析,但为了更好地理解问题本身,并将其扩展到不同的问题设置,我们将以一种更好的形式(概率的角度)来分析这个问题。
在开始时,我们说输出是一个实数值。实际上,我们假设输出是从正态分布中采样得到的,可以通过设置其是以均值为Xw和方差为I(单位方差)的正态分布,如下所示,
现在,我们的目标是找到使输出y似然最大即p(y|X, w)最大化的w。我们定义p(y|X, w) 服从上面的正态分布,其似然函数如下所示:
直接使用似然函数优化是比较困难的,相反,我们将使用和似然函数相同的maxima和minima的对数似然函数。即可以最大化对数似然或最小化负对数似然。 我们选择第二个并称之为损失函数(loss function)。
该损失函数与最小二乘误差函数完全相同。所以我们概率解释了线性回归,这对于下面介绍的模型是非常有帮助的。
MAP解决方法(MAP solution)
上面的解决方法被称为最大似然法,因为这正是我们所做的,使可能性最大化。现在,我们可以把先验概率放在权重上,使w的后验分布最大化,而不是y的似然值。
图显示了MAP方法的流程
在上面的公式中,我们定义权重w的先验是零均值,单位方差的高斯分布,以及使用负对数后验分布来进行损失函数的求解。在这种情况下,w的先验分布试图保持其平均值为0的权重值。这个过程称为L2正则化(岭回归),其在优化时约束权重参数w的值,这可以在损失函数中看到。
先验分布反映了我们对w值的置信度,它不一定是正态分布。如果我们把拉普拉斯分布作为先验,则正则化项将是权重 w(L1正则化 - Lasso)的1-范数。
为了更好地说明正则化效果,我会举一个例子。假设我们有一个具有特征[2,1]和输出3的数据点。对于这个问题,有很多种方法来设置权重从而满足这个式子,但,L2正则化更喜欢权重w的值为[1,1],而L1正则化更喜欢[ 1.5,0],因为[1,1]的2-范数和[1.5,0]的1-范数是所有可能解中最小的那个。因此,我们看到L2正则化尝试尽可能地保持所有权重值接近0。另一方面,L1正则化更喜欢稀疏的解。
泊松回归(Poisson Regression)
我们使用线性回归来处理输出是实数的情况。更具体地说,如果输出值是计数(counts),那么我们可以改变似然分布,并为这个新问题使用相同的设置。泊松分布是模型计数数据的合适分布,我们将使用它。
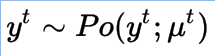
泊松分布的超参数不能取负值。因此,我们稍微改变模型的定义,使用线性模型不直接产生超参数,就像上面正态分布的情况,生成它的对数(实际上是自然对数)。对数是广义线性模型的泊松分布的连接函数,我们又一次用负对数似然函数来优化。
泊松回归的损失函数
我们对损失函数求关于权重w的导数,并将其设为0。就我所知,与线性回归相反,它没有闭合形式解。但是我们可以使用无约束的优化方法来找到迭代的解决方案,下面我为它提供了梯度下降法。在梯度下降法中,我们逐渐更新权重,并在损失梯度的负方向上来进行优化(因为这是损失相对于权重w减小的方向)。
权重w迭代更新公式
Logistic回归(Logistic Regression)
上面我提出了回归问题的模型,但是广义线性模型也可以用于分类问题。在2类分类问题中,似然函数用伯努利分布来定义,即输出为1或0。
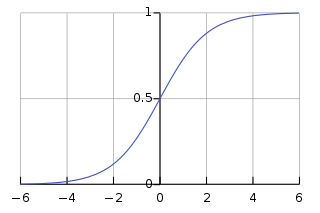
这次我们使用sigmoid函数将线性模型的输出映射到(0,1)的范围,因为伯努利的均值应该在这个范围内。
Sigmoid函数
交叉熵损失函数(Cross-Entropy Loss Function)
上面定义的损失函数被称为交叉熵损失函数,在分类问题中被广泛使用,我们在统计上显示了我们使用它的原因。解决方案没有封闭的表单,我们将使用随机梯度下降(每次更新取一个样本来计算梯度),并提供在线迭代更新机制。
Logistic回归的的随机梯度下降方法
多项Logistic回归(Multinomial Logistic Regression)
如果类数大于2,伯努利分布不足以描述数据。在这种情况下,我们更喜欢多项分布。对于K类分类问题,我们用one-hot编码表示输出。在one-hot编码中,,每个输出都用K维矢量表示,除了取值为1的索引外,其余值全0,这个为1的值表示这个样本的类标。
one-hot编码
这一次,我们定义了y可以属于K个不同概率值。每个类都有自己的概率和权重。因此,与上述模型不同,我们定义了K个不同的权重向量。
公式表示一个输出是从多项式分布被采样得到
每个类的概率都需要大于0,所以我们可以采用线性映射的指数函数,因为它是在泊松回归中完成的。但是这次有K个不同的概率,它们的总和应该等于1。因此,它需要被归一化,为此我们使用softmax函数。
再次,我们使用负对数似然来定义损失函数,它被称为交叉熵损失函数。 类似于泊松回归和Logistic回归,梯度下降优化方法(GradientDescent Optimizer )可以用来解决这个问题。
多项Logistic回归的交叉熵损失函数
在这篇文章中,我试图尽可能地描述清楚各个部分。各个部分的推导过程是很重要的,因为它们形成了更复杂机器学习模型的基础知识,如神经网络。我希望大家能够喜欢。
参考链接:
https://towardsdatascience.com/generalized-linear-models-8738ae0fb97d
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域26个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请扫一扫如下二维码关注我们的公众号,获取人工智能的专业知识!
请加专知小助手微信(Rancho_Fang),加入专知主题人工智能群交流!
点击“阅读原文”,使用专知